Fix a basis { u 1, u 2, u 3} of 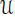 with n( u 1∙ u 2, u 3)= 1 and take v 1:= u 2∙ u 3, v 2:= u 3∙ u 1, v 3:= u 1∙ u 2. Then { v 1, v 2, v 3}is the dual basis in
with n( u 1∙ u 2, u 3)= 1 and take v 1:= u 2∙ u 3, v 2:= u 3∙ u 1, v 3:= u 1∙ u 2. Then { v 1, v 2, v 3}is the dual basis in 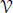 relative to the norm, and the multiplication of the basis { e 1, e 2, u 1, u 2, u 3, v 1, v 2, v 3} is completely determined. For instance, v 1∙ v 2= v 1∙ ( u 3∙ u 1)= − u 3∙ ( v 1∙ u 1)= − u 3∙ (−n( v 1, u 1) e 2) = u 3, …
relative to the norm, and the multiplication of the basis { e 1, e 2, u 1, u 2, u 3, v 1, v 2, v 3} is completely determined. For instance, v 1∙ v 2= v 1∙ ( u 3∙ u 1)= − u 3∙ ( v 1∙ u 1)= − u 3∙ (−n( v 1, u 1) e 2) = u 3, …
The multiplication table is given in Figure 2.1.
The Cayley algebra with this multiplication table is called the split Cayley algebra and denoted by 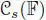 . The subalgebra spanned by e 1, e 2, u 1, v 1is isomorphic to the algebra
. The subalgebra spanned by e 1, e 2, u 1, v 1is isomorphic to the algebra  of 2 × 2 matrices.
of 2 × 2 matrices.
We summarize the above arguments in the next result.
THEOREM 2.2.– There are, up to isomorphism, only three Hurwitz algebras with isotropic norm:  ×
×  ,
,  and
and 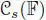 .
.
COROLLARY 2.3.– The real Hurwitz algebras are, up to isomorphism, the following algebras:
– the classical division algebras ℝ, ℂ, ℍ, and ;
– the algebras ℝ × ℝ, and .
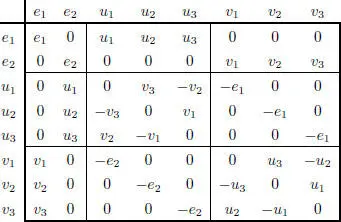
Figure 2.1. Multiplication table of the split Cayley algebra
PROOF.– It is enough to take into account that a non-degenerate quadratic form over ℝ is either isotropic or definite. Hence, the norm of a real Hurwitz algebra is either isotropic or positive definite (as n(1) = 1). □
2.4. Symmetric composition algebras
In this section, a new important family of composition algebras will be described.
DEFINITION 2.2.– A composition algebra (  , ∗, n) is said to be a symmetric composition algebra if
, ∗, n) is said to be a symmetric composition algebra if 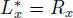 for any (that is , n( x ∗ y , z ) = n( x , y ∗ z ) for any x , y ,
for any (that is , n( x ∗ y , z ) = n( x , y ∗ z ) for any x , y , 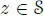 ).
).
THEOREM 2.3.– Let (  , ∗, n) be a composition algebra. The following conditions are equivalent:
, ∗, n) be a composition algebra. The following conditions are equivalent:
1 a) (, ∗, n) is symmetric;
2 b) for any x, , (x ∗ y) ∗ x = x ∗ (y ∗ x) = n(x)y.
The dimension of any symmetric composition algebra is finite, and hence restricted to 1, 2, 4 or 8.
PROOF.– If (  , ∗, n) is symmetric, then for any x , y ,
, ∗, n) is symmetric, then for any x , y , 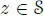 ,
,
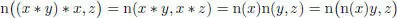
so that  . Also
. Also
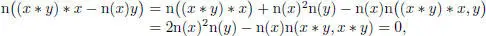
whence (b), since n is non-singular.
Conversely, take x , y ,  with n( y ) ≠ 0, so that Ly and Ry are bijective, and hence there is an element
with n( y ) ≠ 0, so that Ly and Ry are bijective, and hence there is an element  with z = z ʹ ∗ y . Then:
with z = z ʹ ∗ y . Then:
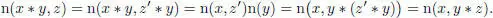
This proves (a) assuming n( y ) ≠ 0, but any isotropic element is the sum of two non-isotropic elements, so (a) follows.
Finally, we can use a modified version of Kaplansky’s trick (see corollary 2.2) as follows. Let 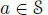 be a norm 1 element and define a new product on
be a norm 1 element and define a new product on  by:
by:

for any x , 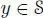 . Then (
. Then (  , ◊, n) is also a composition algebra. Let e = a ∗2. Then, using (b) we have e ◊ x = a ∗ ( a ∗ a )) ∗ ( x ∗ a ) = a ∗ ( x ∗ a ) = x , and similarly x ◊ e = x for any x . Thus, (
, ◊, n) is also a composition algebra. Let e = a ∗2. Then, using (b) we have e ◊ x = a ∗ ( a ∗ a )) ∗ ( x ∗ a ) = a ∗ ( x ∗ a ) = x , and similarly x ◊ e = x for any x . Thus, (  , ◊, n) is a Hurwitz algebra with unity e , and hence it is finite-dimensional. □
, ◊, n) is a Hurwitz algebra with unity e , and hence it is finite-dimensional. □
REMARK 2.4.– Condition (b) above implies that (( x ∗ y ) ∗ x ) ∗ ( x ∗ y ) = n( x ∗ y ) x , but also (( x ∗ y ) ∗ x ) ∗ ( x ∗ y ) = n( x ) y ∗ ( x ∗ y ) = n( x )n( y ) x , so that condition (b) already forces the quadratic form n to be multiplicative.
Читать дальше

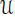 with n( u 1∙ u 2, u 3)= 1 and take v 1:= u 2∙ u 3, v 2:= u 3∙ u 1, v 3:= u 1∙ u 2. Then { v 1, v 2, v 3}is the dual basis in
with n( u 1∙ u 2, u 3)= 1 and take v 1:= u 2∙ u 3, v 2:= u 3∙ u 1, v 3:= u 1∙ u 2. Then { v 1, v 2, v 3}is the dual basis in 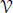 relative to the norm, and the multiplication of the basis { e 1, e 2, u 1, u 2, u 3, v 1, v 2, v 3} is completely determined. For instance, v 1∙ v 2= v 1∙ ( u 3∙ u 1)= − u 3∙ ( v 1∙ u 1)= − u 3∙ (−n( v 1, u 1) e 2) = u 3, …
relative to the norm, and the multiplication of the basis { e 1, e 2, u 1, u 2, u 3, v 1, v 2, v 3} is completely determined. For instance, v 1∙ v 2= v 1∙ ( u 3∙ u 1)= − u 3∙ ( v 1∙ u 1)= − u 3∙ (−n( v 1, u 1) e 2) = u 3, …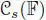 . The subalgebra spanned by e 1, e 2, u 1, v 1is isomorphic to the algebra
. The subalgebra spanned by e 1, e 2, u 1, v 1is isomorphic to the algebra  of 2 × 2 matrices.
of 2 × 2 matrices. ×
× 
 , ∗, n) is said to be a symmetric composition algebra if
, ∗, n) is said to be a symmetric composition algebra if 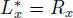 for any (that is , n( x ∗ y , z ) = n( x , y ∗ z ) for any x , y ,
for any (that is , n( x ∗ y , z ) = n( x , y ∗ z ) for any x , y , 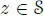 ).
).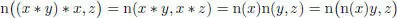
 . Also
. Also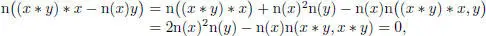
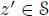 with z = z ʹ ∗ y . Then:
with z = z ʹ ∗ y . Then: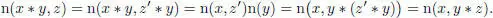
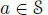 be a norm 1 element and define a new product on
be a norm 1 element and define a new product on 
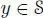 . Then (
. Then ( 










