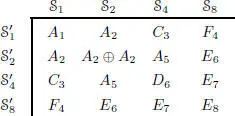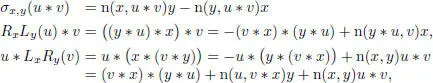
and hence
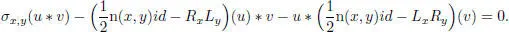
Also 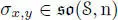 and
and 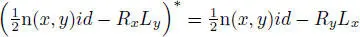 (adjoint relative to the norm n), but RxLx = n( x ) id , so RxLy + RyLx = n( x , y ) id and hence
(adjoint relative to the norm n), but RxLx = n( x ) id , so RxLy + RyLx = n( x , y ) id and hence 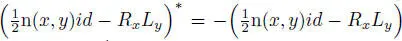 , so that
, so that 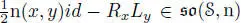 , and
, and 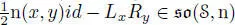 too. Therefore,
too. Therefore, 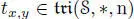 .
.
Since the Lie algebra 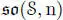 is spanned by the σx , y’s, it is clear that the projection π 0is surjective (and hence so are π 1and π 2). It is not difficult to check that ker π 0= 0, and therefore, π 0is an isomorphism.
is spanned by the σx , y’s, it is clear that the projection π 0is surjective (and hence so are π 1and π 2). It is not difficult to check that ker π 0= 0, and therefore, π 0is an isomorphism.
Finally, the formula [ ta, b , tx , y] = tσa, b (x), y+ tx, σa, b (y)follows from the “same” formula for the σ ’s and the fact that π 0is an isomorphism. □
Given two symmetric composition algebras (  , ∗, n) and
, ∗, n) and 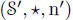 , consider the vector space:
, consider the vector space:
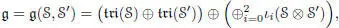
where 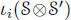 is just a copy of
is just a copy of  ( i = 0, 1, 2) and we write
( i = 0, 1, 2) and we write 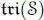 ,
, 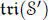 instead of
instead of 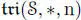 and
and 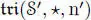 for short. Define now an anticommutative bracket on
for short. Define now an anticommutative bracket on  by means of:
by means of:
– the Lie bracket in , which thus becomes a Lie subalgebra of ;
– [(d0, d1, d2), ιi(x ⊗ x′)] = ιi(di(x) ⊗ x′);
–
– [ιi(x ⊗ x′), ιi+1(y ⊗ y′)] = ιi+2((x ∗ y) ⊗ (x′ ★ y′)) (indices modulo 3);
–
THEOREM 2.9 (Elduque (2004)).– Assume char 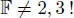 . With the bracket above,
. With the bracket above, 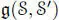 is a Lie algebra and, if
is a Lie algebra and, if 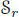 and
and 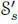 denote symmetric composition algebras of dimension r and s , then the Lie algebra
denote symmetric composition algebras of dimension r and s , then the Lie algebra 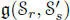 is a (semi) simple Lie algebra whose type is given by Freudenthal’s magic square:
is a (semi) simple Lie algebra whose type is given by Freudenthal’s magic square:
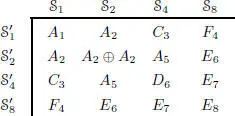
Different versions of this result using Hurwitz algebras instead of symmetric composition algebras have appeared over the years (see Elduque (2004) and the references therein). The advantage of using symmetric composition algebras is that new constructions of the exceptional simple Lie algebras are obtained, and these constructions highlight interesting symmetries due to the different triality automorphisms.
A few changes are needed for characteristic 3. Also, quite interestingly, over fields of characteristic 3 there are non-trivial symmetric composition superalgebras , and these can be plugged into the previous construction to obtain an extended Freudenthal’s magic square that includes some new simple finite dimensional Lie superalgebras (see Cunha and Elduque (2007)).
It is impossible to give a thorough account of composition algebras in a few pages, so many things have had to be left out: Pfister forms and the problem of composition of quadratic forms (see Shapiro (2000)), composition algebras over rings (or even over schemes), where Hurwitz algebras are no longer determined by their norms (see Gille (2014)), the closely related subject of absolute valued algebras (see Rodríguez-Palacios (2004)), etc.
The interested reader may consult the following studies: (Conway and Smith 2003; Springer and Veldkamp 2000; Ebbinghaus et al . 1991; Knus et al . 1998; Okubo 1995). Baez (2002) is a beautiful introduction to octonions and some of their many applications.
Let us conclude with the first words of Okubo in his introduction to the monograph (Okubo 1995):
The saying that God is the mathematician, so that, even with meager experimental support, a mathematically beautiful theory will ultimately have a greater chance of being correct, has been attributed to Dirac. Octonions algebra may surely be called a beautiful mathematical entity. Nevertheless, it has never been systematically utilized in physics in any fundamental fashion, although some attempts have been made toward this goal. However, it is still possible that non-associative algebras (other than Lie algebras) may play some essential future role in the ultimate theory, yet to be discovered.
This work has been supported by grants MTM2017-83506-C2-1-P (AEI/FEDER, UE) and E22 17R (Gobierno de Aragón, Grupo de referencia “Álgebra y Geometría”, co-funded by Feder 2014–2020 “Construyendo Europa desde Aragón”).
Читать дальше

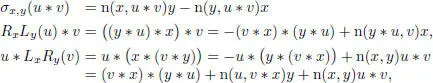
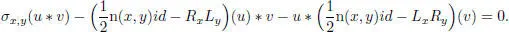
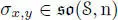 and
and 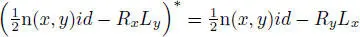 (adjoint relative to the norm n), but RxLx = n( x ) id , so RxLy + RyLx = n( x , y ) id and hence
(adjoint relative to the norm n), but RxLx = n( x ) id , so RxLy + RyLx = n( x , y ) id and hence 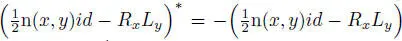 , so that
, so that 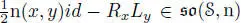 , and
, and 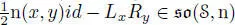 too. Therefore,
too. Therefore, 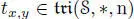 .
.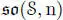 is spanned by the σx , y’s, it is clear that the projection π 0is surjective (and hence so are π 1and π 2). It is not difficult to check that ker π 0= 0, and therefore, π 0is an isomorphism.
is spanned by the σx , y’s, it is clear that the projection π 0is surjective (and hence so are π 1and π 2). It is not difficult to check that ker π 0= 0, and therefore, π 0is an isomorphism. , ∗, n) and
, ∗, n) and 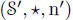 , consider the vector space:
, consider the vector space: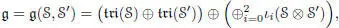
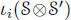 is just a copy of
is just a copy of  ( i = 0, 1, 2) and we write
( i = 0, 1, 2) and we write 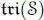 ,
, 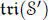 instead of
instead of 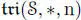 and
and 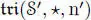 for short. Define now an anticommutative bracket on
for short. Define now an anticommutative bracket on  by means of:
by means of: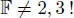 . With the bracket above,
. With the bracket above, 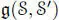 is a Lie algebra and, if
is a Lie algebra and, if 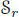 and
and 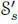 denote symmetric composition algebras of dimension r and s , then the Lie algebra
denote symmetric composition algebras of dimension r and s , then the Lie algebra 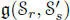 is a (semi) simple Lie algebra whose type is given by Freudenthal’s magic square:
is a (semi) simple Lie algebra whose type is given by Freudenthal’s magic square: