And, as it happens for quaternions, octonions are also present in many interesting geometrical situations, here we mention a few:
– the groups Spin7 and Spin8 (universal covers of SO7(ℝ) and SO8(ℝ)) can be described easily in terms of octonions;
– the fact that is a division algebra implies the parallelizability of the seven-dimensional sphere S7. Actually, S1, S3 and S7 are the only parallelizable spheres (Adams 1958; Bott and Milnor 1958; Kervaire 1958);
– the six-dimensional sphere can be identified with the set of norm 1 imaginary units: , and it is endowed with an almost complex structure, inherited from the multiplication of octonions.
S 2and S 6are the only spheres with such structures (Borel and Serre (1953));
– contrary to what happens in higher dimensions, projective planes do not need to be desarguesian. The simplest example of a non-desarguesian projective plane is the octonionic projective plane .
David R. Wilkins has compiled a large amount of material on the work of Hamilton 1, and for complete expositions on quaternions and octonions, the interested reader may consult Ebbinghaus et al. (1991) and Conway and Smith (2003).
2.3. Unital composition algebras
Composition algebras constitute a generalization of the classical algebras of the real, complex, quaternion and octonion numbers.
A quadratic form n :  on a vector space V over a field
on a vector space V over a field 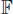 is said to be non-degenerate if its polar form
is said to be non-degenerate if its polar form
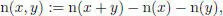
is so, that is, if its radical V ⊥:= { v ∈ V : n( v , V ) = 0} is trivial. Moreover, n is said to be non-singular either if it is non-degenerate or if it satisfies that the dimension of V ⊥is 1 and n( V ⊥) ≠ 0. The last possibility only occurs over fields of characteristic 2.
DEFINITION 2.1.– A composition algebra over a field 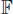 is a triple (
is a triple ( 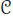 , ∙, n) where
, ∙, n) where
– (, ∙) is a non-associative algebra;
– is a non-singular quadratic form that is multiplicative, that is,
[2.4] 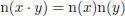
for any x , 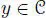 .
.
The unital composition algebras are called Hurwitz algebras .
For simplicity, we will usually refer to the composition algebra 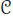 .
.
Our goal in this section is to prove that Hurwitz algebras are quite close to ℝ, ℂ, ℍ and  .
.
By linearization of [2.4], we obtain:
[2.5] 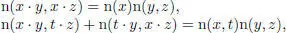
for any x , y , z , 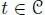 .
.
PROPOSITION 2.2.– Let ( 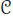 , ∙, n) be a Hurwitz algebra:
, ∙, n) be a Hurwitz algebra:
– either n is non-degenerate or char and is isomorphic to the ground field (with norm α ↦ α2);
– the map is an involution. That is, and for any x, . This involution is referred to as the standard conjugation;
– if ∗ denotes the conjugation of a linear endomorphism relative to n (i.e. n(f(x), y) = n(x, f∗(y)) for any x, y), then for the left and right multiplications by elements we have and ;
– any satisfies the Cayley–Hamilton equation:
– (, ∙) is an alternative algebra: x ∙ (x ∙ y) = x∙2 ∙ y and (y ∙ x) ∙ x = y ∙ x∙2 for any x, .
PROOF.– Plug t = 1 in [2.5]to get

and symmetrically we get 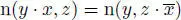 .
.
Now, if char 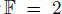 and
and 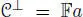 , with n( a ) ≠ 0, then for any x ,
, with n( a ) ≠ 0, then for any x , 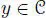 ,
, 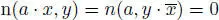 , so
, so  and a ∙ x = f ( x ) a for a linear map
and a ∙ x = f ( x ) a for a linear map 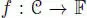 . But n( a )n( x ) = n( a ∙ x ) = f ( x ) 2n( a ). Hence n( x ) = f ( x ) 2for any x and, by linearization, n( x , y ) = 2 f ( x ) f ( y ) = 0 for any x , y . We conclude that
. But n( a )n( x ) = n( a ∙ x ) = f ( x ) 2n( a ). Hence n( x ) = f ( x ) 2for any x and, by linearization, n( x , y ) = 2 f ( x ) f ( y ) = 0 for any x , y . We conclude that 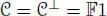 . In this case, all the assertions are trivial.
. In this case, all the assertions are trivial.
Assuming hence that 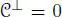 (n is non-degenerate), since
(n is non-degenerate), since  is an isometry of order 2 (reflection relative to
is an isometry of order 2 (reflection relative to 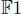 ) we get
) we get
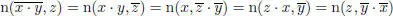
for any x , y , z , whence 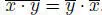 .
.
Читать дальше

 on a vector space V over a field
on a vector space V over a field 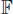 is said to be non-degenerate if its polar form
is said to be non-degenerate if its polar form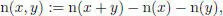
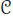 , ∙, n) where
, ∙, n) where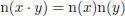
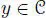 .
.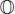 .
.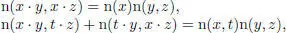
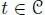 .
.
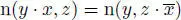 .
.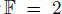 and
and 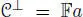 , with n( a ) ≠ 0, then for any x ,
, with n( a ) ≠ 0, then for any x , 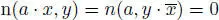 , so
, so  and a ∙ x = f ( x ) a for a linear map
and a ∙ x = f ( x ) a for a linear map 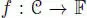 . But n( a )n( x ) = n( a ∙ x ) = f ( x ) 2n( a ). Hence n( x ) = f ( x ) 2for any x and, by linearization, n( x , y ) = 2 f ( x ) f ( y ) = 0 for any x , y . We conclude that
. But n( a )n( x ) = n( a ∙ x ) = f ( x ) 2n( a ). Hence n( x ) = f ( x ) 2for any x and, by linearization, n( x , y ) = 2 f ( x ) f ( y ) = 0 for any x , y . We conclude that 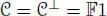 . In this case, all the assertions are trivial.
. In this case, all the assertions are trivial.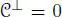 (n is non-degenerate), since
(n is non-degenerate), since  is an isometry of order 2 (reflection relative to
is an isometry of order 2 (reflection relative to  ) we get
) we get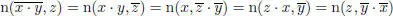
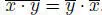 .
.










