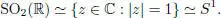Martínez, C., Zelmanov, E.I. (2003). Lie superalgebras graded by P ( n ) and Q ( n ). Proc. Natl. Acad. Sci. USA , 100(14), 8130–8137.
Medvedev, Y.A., Zelmanov, E.I. (1992). Some counterexamples in the theory of Jordan algebras. In Nonassociative Algebraic Models (Zaragoza, 1989) . Nova Science Publishing, Commack, 1–16.
Neveu, A., Schwarz, J. (1971). Factorizable dual model of pions. Nuclear Physics B , 31(1), 86–112.
Racine, M.L., Zelmanov, E.I. (2003). Simple Jordan superalgebras with semisimple even part. J. Algebra , 270(2), 374–444.
Racine, M.L., Zelmanov, E.I. (2015). An octonionic construction of the Kac superalgebra K 10. Proc. Amer. Math. Soc ., 143(3), 1075–1083.
Ramond, P. (1971). Dual theory for free fermions. Phys. Rev. D , 3, 2415–2418.
Schoutens, K. (1987). A nonlinear representation of the d = 2 SO(4) extended superconformal algebra. Phys. Lett ., B194, 75–80.
Schwimmer, A., Seiberg, N. (1987). Comments on the n = 2, 3, 4 superconformal algebras in two dimensions. Physics Letters B , 184(2), 191–196.
Shestakov, I.P. (1997). Prime alternative superalgebras of arbitrary characteristic. Algebra i Logika . 36(6), 675–716, 722.
Shtern, A.S. (1987). Representations of an exceptional Jordan superalgebra. Funktsional. Anal. i Prilozhen ., 21(3), 93–94.
Solarte, O.F., Shestakov, I. (2016). Irreductible representations of the simple Jordan superalgebra of Grassmann Poisson bracket. J. Algebra , 455, 29–313.
Stern, A.S. (1995). Representations of finite-dimensional Jordan superalgebras of Poisson brackets. Comm. Algebra , 23(5), 1815–1823.
Tits, J. (1962). Une classe d’algèbres de Lie en relation avec les algèbres de Jordan. Nederl. Akad. Wetensch. Proc ., A 65, 24, 530–535.
Tits, J. (1966). Algèbres alternatives, algèbres de Jordan et algèbres de Lie exceptionnelles. I. Construction. Nederl. Akad. Wetensch. Proc ., A 69, 28, 223–237.
Trushina, M. (2008). Modular representations of the Jordan superalgebras D ( t ) and K 3. J. Algebra , 320(4), 1327–1343.
Wall, C.T.C. (1963, 1964). Graded Brauer groups. J. Reine Angew. Math ., 213, 187–199.
Zelmanov, E. (2000). Semisimple finite dimensional Jordan superalgebras. In Combinatorial and Computational Algebra , Chan, K.Y., Mikhalev, A.A., Siu, M.-K., Yu, J.-T., Zelmanov, E. (eds). American Mathematical Society, Providence, 227–243.
Zhevlakov, K.A., Slin’ko, A.M., Shestakov, I.P., Shirshov, A.I. (1982). Rings That are Nearly Associative (Translated by H.F. Smith). Academic Press, Inc., New York.
Alberto ELDUQUE
Department of Mathematics, University of Zaragoza, Spain
Unital composition algebras are the analogues of the classical algebras of the real and complex numbers, quaternions and octonions, but the class of composition algebras have been recently enriched with new algebras, mainly the so-called symmetric composition algebras, which play an effective role in understanding the triality phenomenon in dimension 8. The goal of this chapter is to examine the main definitions and results of these algebras.
Section 2.2reviews the discovery of the real algebra of quaternions by Hamilton, surveys some of the applications of quaternions to deal with rotations in three- and four-dimensional euclidean spaces and then examines octonions, discovered shortly after Hamilton’s breakthrough.
Section 2.3is devoted to the classification of the unital composition algebras, also known as Hurwitz algebras. This is achieved by means of the Cayley–Dickson doubling process, which mimics the way in which Graves and Cayley constructed the octonions by doubling the quaternions. Hurwitz algebra itself, in 1898, proved that a positive definite quadratic form over the real numbers allows composition if and only if the dimension is restricted to 1, 2, 4 or 8. These are the possible dimensions of Hurwitz algebras over arbitrary fields, and of finite-dimensional non-unital composition algebras. Some attention is paid to the case of Hurwitz algebras with isotropic norm, as this is instrumental in defining Okubo algebras later on, although the model of Zorn’s vector matrices is not touched upon.
In section 2.4, symmetric composition algebras are defined. In dimension > 1, these are non-unital composition algebras, satisfying the extra condition of “associativity of the norm”: n ( x ∗ y , z ) = n ( x , y ∗ z ). The interest lies in dimension 8, where these algebras split into two disjoint families: para-Hurwitz algebras and Okubo algebras. The existence of the latter Okubo algebras justifies the introduction of the symmetric composition algebras.
Formulas for triality are simpler if one uses symmetric composition algebras instead of the classical Hurwitz algebras. This is examined in section 2.5. Triality is a broad subject. In projective geometry, there is duality relating points and hyperplanes. Given a vector space of dimension 8, endowed with a quadratic form q with maximal Witt index, the quadric of isotropic vectors 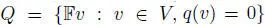 in projective space ℙ( V ) contains points, lines, planes and “solids”, and there are two kinds of “solids”. Geometric triality relates points and the two kinds of solids in a cyclic way. This goes back to Study (1913) and Cartan (1925). Tits (1959) showed that there are two different types of geometric trialities; one is related to octonions (or para-octonions) and the exceptional group G 2, while the other is related to the classical groups of type A 2, unless the characteristic is 3. The algebras hidden behind this second type are the Okubo algebras. From the algebraic point of view, triality relates the natural and spin representations of the spin group on an eight-dimensional quadratic space, that is the three irreducible representations corresponding to the outer vertices of the Dynkin diagram D 4. Here, we will consider lightly the local version of triality, which gives a very symmetric construction of Freudenthal’s magic square.
in projective space ℙ( V ) contains points, lines, planes and “solids”, and there are two kinds of “solids”. Geometric triality relates points and the two kinds of solids in a cyclic way. This goes back to Study (1913) and Cartan (1925). Tits (1959) showed that there are two different types of geometric trialities; one is related to octonions (or para-octonions) and the exceptional group G 2, while the other is related to the classical groups of type A 2, unless the characteristic is 3. The algebras hidden behind this second type are the Okubo algebras. From the algebraic point of view, triality relates the natural and spin representations of the spin group on an eight-dimensional quadratic space, that is the three irreducible representations corresponding to the outer vertices of the Dynkin diagram D 4. Here, we will consider lightly the local version of triality, which gives a very symmetric construction of Freudenthal’s magic square.
2.2. Quaternions and octonions
It is safe to say that the history of composition algebras starts with the discovery of the real quaternions by Hamilton.
Real and complex numbers are in the toolkit of any scientist. Complex numbers correspond to vectors in a Euclidean plane, so that addition and multiplication by real scalars are the natural ones for vectors. The length (or modulus, or norm) of the product of two complex numbers is the product of the lengths of the factors. In this way, multiplication by a norm 1 complex number is an isometry, actually a rotation, of the plane, and this allows us to identify the group of rotations of the Euclidean plane, that is, the special orthogonal group SO 2(ℝ), with the set of norm one complex numbers (the unit circle):
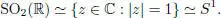
In 1835, William Hamilton posed himself the problem of extending the domain of complex numbers to a system of numbers “of dimension 3”. He tried to find a multiplication, analogous to the multiplication of complex numbers, but in dimension 3, that should respect the “law of moduli”:
Читать дальше

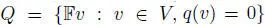 in projective space ℙ( V ) contains points, lines, planes and “solids”, and there are two kinds of “solids”. Geometric triality relates points and the two kinds of solids in a cyclic way. This goes back to Study (1913) and Cartan (1925). Tits (1959) showed that there are two different types of geometric trialities; one is related to octonions (or para-octonions) and the exceptional group G 2, while the other is related to the classical groups of type A 2, unless the characteristic is 3. The algebras hidden behind this second type are the Okubo algebras. From the algebraic point of view, triality relates the natural and spin representations of the spin group on an eight-dimensional quadratic space, that is the three irreducible representations corresponding to the outer vertices of the Dynkin diagram D 4. Here, we will consider lightly the local version of triality, which gives a very symmetric construction of Freudenthal’s magic square.
in projective space ℙ( V ) contains points, lines, planes and “solids”, and there are two kinds of “solids”. Geometric triality relates points and the two kinds of solids in a cyclic way. This goes back to Study (1913) and Cartan (1925). Tits (1959) showed that there are two different types of geometric trialities; one is related to octonions (or para-octonions) and the exceptional group G 2, while the other is related to the classical groups of type A 2, unless the characteristic is 3. The algebras hidden behind this second type are the Okubo algebras. From the algebraic point of view, triality relates the natural and spin representations of the spin group on an eight-dimensional quadratic space, that is the three irreducible representations corresponding to the outer vertices of the Dynkin diagram D 4. Here, we will consider lightly the local version of triality, which gives a very symmetric construction of Freudenthal’s magic square.