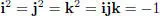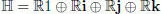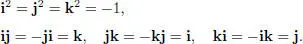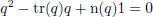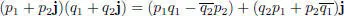[2.1] 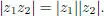
That is, he tried to get a formula for

and assumed i 2= j 2= −1. The problem is how to define ijand ji.
With some “modern” insight, it is easy to see that this is impossible. A non-associative (i.e. not necessarily associative) algebra over a field 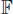 is just a vector space
is just a vector space 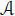 over
over 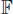 , endowed with a bilinear map (the multiplication)
, endowed with a bilinear map (the multiplication) 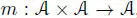 , ( x , y ) ↦ xy . We will refer to the algebra (
, ( x , y ) ↦ xy . We will refer to the algebra ( 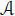 , m ) or simply
, m ) or simply 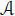 if no confusion arises. The algebra
if no confusion arises. The algebra 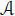 is said to be a division algebra if the left and right multiplications, Lx : y ↦ xy , Rx : y ↦ yx , are bijective for any non-zero x ∈
is said to be a division algebra if the left and right multiplications, Lx : y ↦ xy , Rx : y ↦ yx , are bijective for any non-zero x ∈ 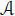 . The “law of moduli” forces the algebra sought for by Hamilton to be a division algebra. But this is impossible.
. The “law of moduli” forces the algebra sought for by Hamilton to be a division algebra. But this is impossible.
PROPOSITION 2.1.– There are no real division algebras of odd dimension ≥ 3.
PROOF (See Petersson (2005)).– Given a real algebra 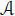 of odd dimension ≥ 3, and linearly independent elements x , y ∈
of odd dimension ≥ 3, and linearly independent elements x , y ∈ 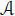 with Lx and Ly bijective, det( Lx + tLy ) is a polynomial in t of odd degree, and hence it has a real root λ. Thus, the left multiplication Lx + λyis not bijective. □
with Lx and Ly bijective, det( Lx + tLy ) is a polynomial in t of odd degree, and hence it has a real root λ. Thus, the left multiplication Lx + λyis not bijective. □
Therefore, Hamilton could not succeed. But, after years of struggle, he discovered how to overcome the difficulties in dimension 3 by making a leap to dimension 4.
In a letter (Wilkins 2020) to his son Archibald, dated August 5, 1865, Hamilton explained how vividly he remembered the date: October 16, 1843 , when he got the key idea. He wrote:
Every morning in the early part of the above-cited month, on my coming down to breakfast, your (then) little brother William Edwin, and yourself, used to ask me, “Well, Papa, can you multiply triplets”? Whereto I was always obliged to reply, with a sad shake of the head: “No, I can only add and subtract them.”
But on the 16th day of the same month – which happened to be a Monday, and a Council day of the Royal Irish Academy – I was walking in to attend and preside, and your mother was walking with me, along the Royal Canal, to which she had perhaps driven; although she talked with me now and then, yet an undercurrent of thought was going on in my mind, which gave at last a result, whereof it is not too much to say that I felt at once the importance. An electric circuit seemed to close; and a spark flashed forth, the herald (as I foresaw, immediately) of many long years to come of definitely directed thought and work, by myself if spared, and at all events on the part of others, if I should even be allowed to live long enough distinctly to communicate the discovery.
Nor could I resist the impulse – unphilosophical as it may have been – to cut with a knife on a stone of Brougham Bridge, as we passed it, the fundamental formula with the symbols, i, j, k, namely,
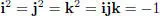
which contains the solution of the problem, but of course, as an inscription, has long since mouldered away. A more durable notice remains, however, on the Council Books of the Academy for that day (October 16, 1843), which records the fact, that I then asked for and obtained leave to read a Paper on ‘Quaternions’, at the first general meeting of the session: which reading took place accordingly, on Monday, November 13 following.
Hamilton realized that the product ijhad to be linearly independent of 1, i, j, and hence he defined the real algebra of quaternions as:
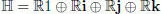
with multiplication determined by
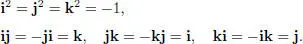
Some properties of this algebra are summarized as follows:
– For any q1, q2 ∈ ℍ, |q1q2 | = |q1||q2| ∀q1, q2 ∈ ℍ, where for q = a + bi + cj + ck, |a + bi + cj + dk|2 = a2 + b2 + c2 + d2 is the standard Euclidean norm on ℍ ≃ ℝ4.
– ℍ is an associative division algebra, but we lose the commutativity valid for the real and complex numbers.
Therefore, S 3≃ { q ∈ ℍ : | q | = 1} is a (Lie) group. This implies the parallelizability of the three-dimensional sphere S 3.
– ℍ splits as ℍ = ℝ1 ⊕ ℍ0, where ℍ0 = ℝi ⊕ ℝj ⊕ ℝk is the subspace of purely imaginary quaternions.
Then, for any u , v ∈ ℍ 0:

where u ∙ v and u × v denote the usual scalar and cross-products in ℝ 3≃ ℍ 0.
– For any q = a1 + u ∈ ℍ(u ∈ ℍ0), q2 = (a2 − u ∙ u) + 2au, so
[2.2] 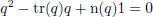
with tr( q )= 2 a and n( q ) = | q | 2= a 2+ u ∙ u . That is, ℍ is a quadratic algebra .
– The map is an involution, with and .
– ℍ = ℂ ⊕ ℂj ≃ ℂ2 is a two-dimensional vector space over ℂ. The multiplication is then given by:
[2.3] 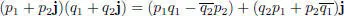
for any p 1, p 2, q 1, q 2∈ ℂ.
2.2.2. Rotations in three- ( and four- ) dimensional space
Читать дальше

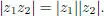

 is just a vector space
is just a vector space 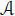 over
over 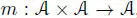 , ( x , y ) ↦ xy . We will refer to the algebra (
, ( x , y ) ↦ xy . We will refer to the algebra (