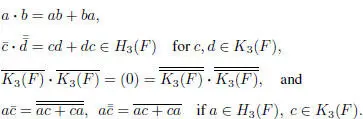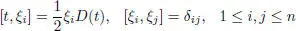
can be extended to a contact bracket on Λ(1 : n ).
DEFINITION 1.12.– [Kantor double] Let A be an associative commutative superalgebra with a bilinear map { , } : A × A → A. Assume that 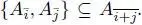 . Consider a direct sum of vector spaces KJ( A , { , }) = A + Av where | v | = 1. Define a new product in J (A, { , }) that coincides with the original one in A and is given by :
. Consider a direct sum of vector spaces KJ( A , { , }) = A + Av where | v | = 1. Define a new product in J (A, { , }) that coincides with the original one in A and is given by :
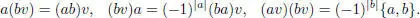
The superalgebra KJ( A , { , }) is called the Kantor double of ( A , { , }).
Kantor (1990) proved that if the bracket { , } is a Poisson bracket, then KJ( A , { , }) is a Jordan superalgebra.
DEFINITION 1.13.– The bilinear map { , } is called a Jordan bracket on the superalgebra A if KJ( A , { , }) is a Jordan superalgebra ( see King and McCrimmon (1992 )).
Cantarini and Kac (2007) showed that there is a 1-1 correspondence between Jordan brackets and contact brackets. Indeed, if [ a, b ] is a contact bracket with derivation D , D ( a ) = [ a , 1], then the new bracket
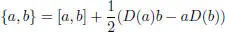
is a Jordan bracket.
Applying this to example 1.19, we get the following:
EXAMPLE 1.20.– The values { ξi , t } = 0, { ξi , ξj } = δij for 1 ≤ i , j ≤ n extend to a Jordan bracket of Λ(1 : n ). Applying the Kantor double process to this bracket, we get Jordan superalgebras Jn = KJ(Λ(1 : n ), { , }).
1.5. Cheng–Kac superalgebras
Given an arbitrary unital associative commutative (super)-algebra with an (even) derivation d : Z → Z , Martínez and Zelmanov constructed (Martínez and Zelmanov 2010) a Jordan superalgebra JCK( Z, d ) named the Cheng–Kac Jordan superalgebra.
The even part of JCK( Z , d ) is a rank 4 free module over Z with basis {1, w 1, w 2, w 3}, 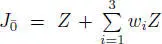 , and multiplication given by wiwj = 0 if 1 ≤ i ≠ j ≤ 3,
, and multiplication given by wiwj = 0 if 1 ≤ i ≠ j ≤ 3, 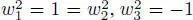 . The odd part of this superalgebra is also a rank 4 free module over Z with basis { x , x 1, x 2, x 3},
. The odd part of this superalgebra is also a rank 4 free module over Z with basis { x , x 1, x 2, x 3},  .
.
The action of the even part on the odd part and the products of two elements, respectively, are given by the following multiplication tables:
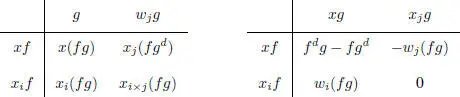
where xi × i = 0, x 1 × 2= – x 2 × 1= x 3, x 1 × 3= – x 3 × 1= x 2, – x 2 × 3= x 1= x 3 × 2.
The superalgebra JCK( Z , d ) is simple if and only if Z is d -simple, that is, Z does not contain proper d -invariant ideals (see Martínez and Zelmanov (2010)).
Let us remark that for Z = ℂ[ t , t –1] the above construction leads to the Cheng–Kac superconformal algebra, that is, CK( 6 ) = TKK(JCK( 6 )), where
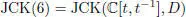
with 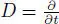 (see section 1.8).
(see section 1.8).
1.6. Finite dimensional simple Jordan superalgebras
1.6.1. Case F is algebraically closed and char F = 0
Let us assume now that F is algebraically closed and char F = 0. Kac derived the classification of finite dimensional simple Jordan F -superalgebras from his classification of simple finite dimensional Lie superalgebras via the Tits–Kantor–Koecher construction.
THEOREM 1.1 (see Kac (1977a) and Kantor (1990)).– Let 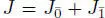 be a simple Jordan superalgebra over an algebraically closed field F , char F = 0. Then J is isomorphic to one of the superalgebras in examples 1.8, 1.9and 1.10– 1.15or it is the Kantor double of the Poisson bracket in example 1.17.
be a simple Jordan superalgebra over an algebraically closed field F , char F = 0. Then J is isomorphic to one of the superalgebras in examples 1.8, 1.9and 1.10– 1.15or it is the Kantor double of the Poisson bracket in example 1.17.
REMARK 1.3.– We will assume always in this section that 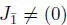 .
.
1.6.2. Case char F = p > 2, the even part 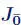 is semisimple
is semisimple
Let us assume next that char F = p > 2 and the even part 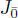 is a semisimple Jordan algebra.
is a semisimple Jordan algebra.
Recall that a semisimple Jordan algebra is a direct sum of finitely many simple ideals.
This case was addressed in Racine and Zelmanov (2003) and the classification essentially coincides with the one of zero characteristic, expect of some differences if char F = 3.
EXAMPLE 1.21.– Let H 3( F ), K 3( F ) denote the symmetric and skew-symmetric 3×3 matrices over F , char F = 3. Consider  and
and 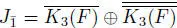 the sum of two copies of K 3( F ). We have a Jordan superalgebra structure on
the sum of two copies of K 3( F ). We have a Jordan superalgebra structure on 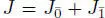 via a ∙ b = a ∙ b in M3 ( F ) +if a , b ∈ H3 ( F ), that is,
via a ∙ b = a ∙ b in M3 ( F ) +if a , b ∈ H3 ( F ), that is,
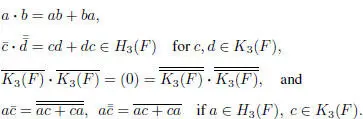
This superalgebra is simple.
Читать дальше

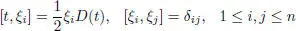
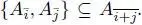 . Consider a direct sum of vector spaces KJ( A , { , }) = A + Av where | v | = 1. Define a new product in J (A, { , }) that coincides with the original one in A and is given by :
. Consider a direct sum of vector spaces KJ( A , { , }) = A + Av where | v | = 1. Define a new product in J (A, { , }) that coincides with the original one in A and is given by :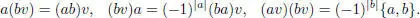
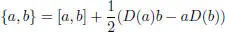
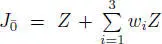 , and multiplication given by wiwj = 0 if 1 ≤ i ≠ j ≤ 3,
, and multiplication given by wiwj = 0 if 1 ≤ i ≠ j ≤ 3, 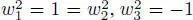 . The odd part of this superalgebra is also a rank 4 free module over Z with basis { x , x 1, x 2, x 3},
. The odd part of this superalgebra is also a rank 4 free module over Z with basis { x , x 1, x 2, x 3},  .
.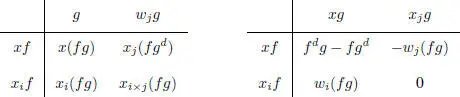
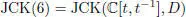
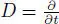 (see section 1.8).
(see section 1.8).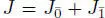 be a simple Jordan superalgebra over an algebraically closed field F , char F = 0. Then J is isomorphic to one of the superalgebras in examples 1.8, 1.9and 1.10– 1.15or it is the Kantor double of the Poisson bracket in example 1.17.
be a simple Jordan superalgebra over an algebraically closed field F , char F = 0. Then J is isomorphic to one of the superalgebras in examples 1.8, 1.9and 1.10– 1.15or it is the Kantor double of the Poisson bracket in example 1.17. .
.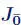 is semisimple
is semisimple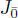 is a semisimple Jordan algebra.
is a semisimple Jordan algebra. and
and 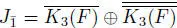 the sum of two copies of K 3( F ). We have a Jordan superalgebra structure on
the sum of two copies of K 3( F ). We have a Jordan superalgebra structure on