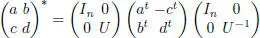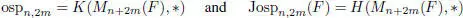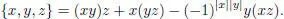
Note that every algebra is a superalgebra with the trivial grading, that is, 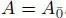 .
.
1.2. Tits–Kantor–Koecher construction
Tits (1962, 1966) made an important observation that relates Lie and Jordan structures. Let L be a Lie superalgebra whose even part 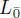 contains an
contains an 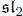 -triple { e, f, h }, that is,
-triple { e, f, h }, that is,
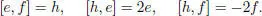
DEFINITION 1.6.– An 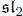 -triple e , f , h is said to be “good” if ad ( h ) : L → L is diagonalizable and the eigenvalues are only –2, 0, 2.
-triple e , f , h is said to be “good” if ad ( h ) : L → L is diagonalizable and the eigenvalues are only –2, 0, 2.
In such a case, L = L – 2+ L 0+ L 2decomposes as a direct sum of eigenspaces. We can define a new product in L 2by:
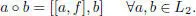
With this new product, J = ( L 2, ○ ) becomes a Jordan superalgebra.
Moreover, (Tits 1962, 1966; Kantor 1972) and (Koecher 1967) showed that every Jordan superalgebra can be obtained in this way. The corresponding Lie superalgebra is not unique, but any two such Lie superalgebras are centrally isogenous, that is, they have the same central cover. Let us recall the construction of L = TKK( J ), the universal Lie superalgebra in this class (see Martin and Piard (1992)).
CONSTRUCTION.– Consider J a unital Jordan superalgebra, and { ei } i∈Ia basis of J .
Let
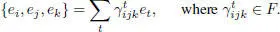
Define a Lie superalgebra K by generators 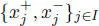 and relations
and relations
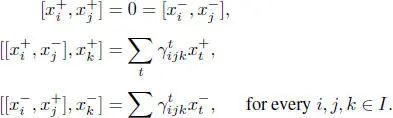
This Lie superalgebra has a short grading K = K –1+ K 0+ K 1where
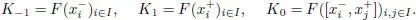
K is the universal Tits–Kantor–Koecher Lie superalgebra of the unital Jordan superalgebra J :
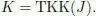
1.3. Basic examples (classical superalgebras)
Let  be an associative superalgebra. The new operation in the underlying vector space A given by:
be an associative superalgebra. The new operation in the underlying vector space A given by:
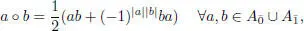
defines a structure of a Jordan superalgebra on A that is denoted A (+).
DEFINITION 1.7.– Those Jordan superalgebras that can be obtained as subalgebras of a superalgebra A (+), with A an associative superalgebra, are called special. Superalgebras that are not special are called exceptional .
REMARK 1.2.– If we consider in the original associative superalgebra the new product given by:
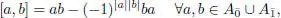
we get a Lie superalgebra that is denoted as A (–).
DEFINITION 1.8.– A superalgebra A is simple if it does not have non-trivial graded ideals. A graded ideal is an ideal I ⊴ A such that for every a = a 0+ a 1∈ I, it follows that a 0, a 1∈ I . So every graded ideal I satisfies 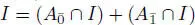 .
.
Wall (1963, 1964) proved that an arbitrary simple finite dimensional superalgebra over an algebraically closed field is isomorphic to one of the following two types:
1 I) .
2 II) .
Consequently, we can easily get the first examples of simple finite dimensional Jordan superalgebras as explained above.
EXAMPLE 1.8.– 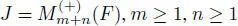 .
.
EXAMPLE 1.9.– J = Q ( n ) (+), n ≥ 2.
DEFINITION 1.9.– Let A be an associative superalgebra . A map ∗ : A → A is a superinvolution if it satisfies :
1 i) (a∗)∗ = a, ∀a ∈ A;
2 ii) .
If ∗ : A → A is a superinvolution of the associative superalgebra A , then the set of symmetric elements H ( A , ∗) is a Jordan superalgebra of A (+). Similarly, the subspace of skew-symmetric elements K ( A , ∗)= { a ∈ A | a ∗= – a } is a Lie subsuperalgebra of A (–).
The following two subsuperalgebras of 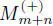 are of this type.
are of this type.
EXAMPLE 1.10.– Let In , Im be the identity matrices and let t be the transposition.
Let us denote 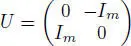 .
.
Then U t = U –1= – U , and ∗ : Mn+ 2m( F ) → Mn+ 2m( F ) given by
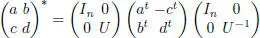
is a superinvolution.
The superalgebras
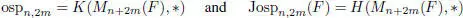
are the Lie and Jordan orthosymplectic superalgebras, respectively.
EXAMPLE 1.11.– The associative superalgebra Mn+n ( F ) has another superinvolution given by:
Читать дальше

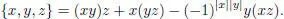
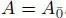 .
. contains an
contains an  -triple { e, f, h }, that is,
-triple { e, f, h }, that is,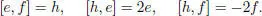
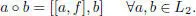
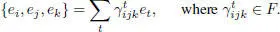
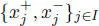 and relations
and relations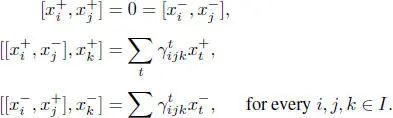
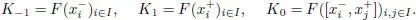
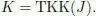
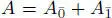 be an associative superalgebra. The new operation in the underlying vector space A given by:
be an associative superalgebra. The new operation in the underlying vector space A given by: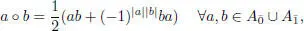
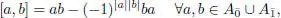
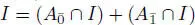 .
.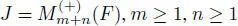 .
.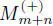 are of this type.
are of this type.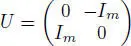 .
.