DEFINITION 1.1.– A (linear ) Jordan algebra is a vector space J with a linear binary operation ( x , y ) ↦ xy satisfying the following identities :
(J1) xy = yx (commutativity );
(J2) ( x 2 y ) x = x 2( yx ) ∀ x, y ∈ J (Jordan identity ).
Instead of (J2 ) we can consider the corresponding linearized identity :
( J’2 ) ( xy )( zu ) + (xz )( yu ) + (xu )( yz ) = (( xy ) z ) u + (( xu ) z ) y + (( yu ) z ) x ∀ x, y, z, u ∈ J .
REMARK 1.1.– A Lie algebra L is a vector space with a linear binary operation ( x, y ) ↦ [ x, y ] satisfying the following identities:
(L1) [ x, y ] = – [y, x ] (anticommutativity);
(L2) [[ x, y ], z ] + [[ y, z ], x ] + [[ z, x ], y ] = 0 for arbitrary elements x , y , z ∈ J (Jacobi identity).
EXAMPLE 1.1.– If A is an associative algebra, then ( A (+), ∙), where a ∙ b = ab + ba is a Jordan algebra, and ( A (–), [, ]), where [ a, b ] = ab – ba is a Lie algebra. Both A (+)and A (–)have the same underlying vector space as A .
DEFINITION 1.2.– A superalgebra A is an algebra with a ℤ /2 ℤ-grading. So 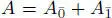 is a direct sum of two vector spaces and
is a direct sum of two vector spaces and
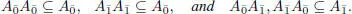
Elements of 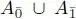 are called homogeneous elements. The parity of a homogeneous element a, denoted | a |, is defined by | a | = 0 if
are called homogeneous elements. The parity of a homogeneous element a, denoted | a |, is defined by | a | = 0 if 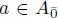 and | a | = 1 if
and | a | = 1 if 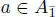 .
.
Elements in 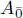 are called even and elements in
are called even and elements in 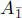 are called odd .
are called odd .
Note that 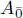 is a subalgebra of A, but
is a subalgebra of A, but 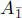 is not, instead it can be seen as a bimodule over
is not, instead it can be seen as a bimodule over 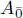 .
.
EXAMPLE 1.2.– If V is a vector space of countable dimension, then G = G(V ) denotes the Grassmann (or exterior) algebra over V , that is, the quotient of the tensor algebra over the ideal generated by the symmetric tensors v ⊗ w + w ⊗ v , v , w ∈ V . This algebra G(V ) is ℤ/ 2 ℤ -graded. Indeed, 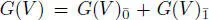 , where the “even part” is the linear span of all tensors of even length and the “odd part”
, where the “even part” is the linear span of all tensors of even length and the “odd part” 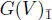 is the linear span of all tensors of odd length.
is the linear span of all tensors of odd length.
G(V ) is an example of a superalgebra.
DEFINITION 1.3.– Consider a variety of algebras V defined by homogeneous identities (see Jacobson (1968 ) or Zhevlakov et al. ( 1982 )). We say that a superalgebra 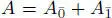 is a V-superalgebra if the even part of A ⊗ F G(V ) lies in the variety, that is
is a V-superalgebra if the even part of A ⊗ F G(V ) lies in the variety, that is

DEFINITION 1.4.– The algebra 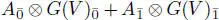 is called the Grassmann envelope of the superalgebra A and will be denoted as G ( A ).
is called the Grassmann envelope of the superalgebra A and will be denoted as G ( A ).
Let us consider V the variety of associative, commutative, anticommutative, Jordan or Lie algebras, respectively. Then we get:
EXAMPLE 1.3.– A superalgebra 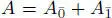 is an associative superalgebra if and only if it is a ℤ/2ℤ-graded associative algebra.
is an associative superalgebra if and only if it is a ℤ/2ℤ-graded associative algebra.
EXAMPLE 1.4.– A superalgebra 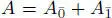 is a commutative superalgebra if it satisfies:
is a commutative superalgebra if it satisfies:
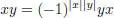
for any x , y homogeneous elements of A .
EXAMPLE 1.5.– A superalgebra A is an anticommutative superalgebra if
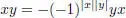
for every x , y homogeneous elements of A .
EXAMPLE 1.6.– A Jordan superalgebra is a superalgebra that is commutative and satisfies the graded identity:
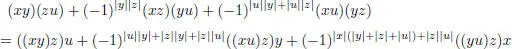
for every homogeneous elements 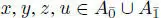 .
.
EXAMPLE 1.7.– An anticommutative superalgebra A is a Lie superalgebra if it satisfies:
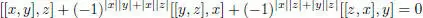
for every 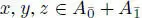 .
.
DEFINITION 1.5.– If 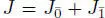 is a Jordan superalgebra and , then their triple product is defined by :
is a Jordan superalgebra and , then their triple product is defined by :
Читать дальше

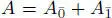 is a direct sum of two vector spaces and
is a direct sum of two vector spaces and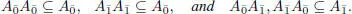
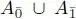 are called homogeneous elements. The parity of a homogeneous element a, denoted | a |, is defined by | a | = 0 if
are called homogeneous elements. The parity of a homogeneous element a, denoted | a |, is defined by | a | = 0 if 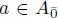 and | a | = 1 if
and | a | = 1 if 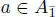 .
.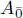 are called even and elements in
are called even and elements in 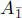 are called odd .
are called odd .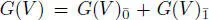 , where the “even part” is the linear span of all tensors of even length and the “odd part”
, where the “even part” is the linear span of all tensors of even length and the “odd part” 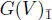 is the linear span of all tensors of odd length.
is the linear span of all tensors of odd length.
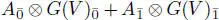 is called the Grassmann envelope of the superalgebra A and will be denoted as G ( A ).
is called the Grassmann envelope of the superalgebra A and will be denoted as G ( A ).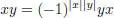
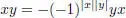
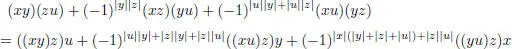
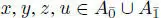 .
.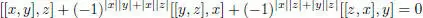
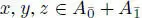 .
.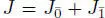 is a Jordan superalgebra and , then their triple product is defined by :
is a Jordan superalgebra and , then their triple product is defined by :










