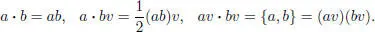EXAMPLE 1.22.– Let 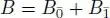 with
with 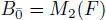 ,
, 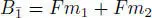 , where F is a field, char F = 3. The product in
, where F is a field, char F = 3. The product in 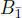 is given by:
is given by:
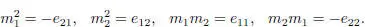
The action of 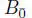 over
over 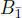 is defined as follows:
is defined as follows:
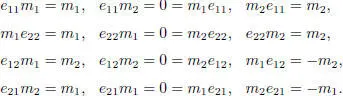
Shestakov (1997) proved that B is an alternative superalgebra and has a natural involution ∗ given by ( a + m )∗ = ā – m , 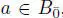 , where a ↦ ā is the symplectic involution, and
, where a ↦ ā is the symplectic involution, and 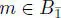 .
.
If H 3( B , ∗) denotes the symmetric matrices with respect to the involution ∗, then H 3( B , ∗) is a simple Jordan superalgebra. It is i -exceptional, that is, it is not a homomorphic image of a special Jordan superalgebra.
THEOREM 1.2 (Racine and Zelmanov (2003)).– Let 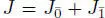 be a finite dimensional central simple Jordan superalgebra over an algebraically closed field F of char F = p > 2. If
be a finite dimensional central simple Jordan superalgebra over an algebraically closed field F of char F = p > 2. If 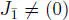 and
and 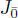 is semisimple, then J is isomorphic to one of the superalgebras in examples 1.8, 1.9, 1.10– 1.14or char F = 3 and J is the nine-dimensional degenerate Kac superalgebra (see example 1.15) or J is isomorphic to one of the superalgebras in examples 1.21and 1.22.
is semisimple, then J is isomorphic to one of the superalgebras in examples 1.8, 1.9, 1.10– 1.14or char F = 3 and J is the nine-dimensional degenerate Kac superalgebra (see example 1.15) or J is isomorphic to one of the superalgebras in examples 1.21and 1.22.
1.6.3. Case char F = p > 2, the even part 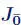 is not semisimple
is not semisimple
This case shows similarities with infinite dimensional superconformal Jordan algebras (see section 1.8) in characteristic 0.
Let us denote  the algebra of truncated polynomials in m variables. Let B ( m, n ) = B ( m ) ⊗ G ( n ) be the tensor product of B ( m ) with the Grassmann algebra G ( n ) = 〈 1, ξ 1,…, ξn 〉. Then B ( m, n ) is an associative commutative superalgebra.
the algebra of truncated polynomials in m variables. Let B ( m, n ) = B ( m ) ⊗ G ( n ) be the tensor product of B ( m ) with the Grassmann algebra G ( n ) = 〈 1, ξ 1,…, ξn 〉. Then B ( m, n ) is an associative commutative superalgebra.
THEOREM 1.3 (Martínez and Zelmanov (2010)).– Let 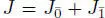 be a finite dimensional simple unital Jordan superalgebra over an algebraically closed field F of characteristic p > 2. If the even part
be a finite dimensional simple unital Jordan superalgebra over an algebraically closed field F of characteristic p > 2. If the even part 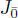 is not semisimple, then there exist integers m , n and a Jordan bracket { , } on B ( m, n ) such that J = B ( m , n ) + B ( m , n ) v = KJ( B ( m , n ), { , }) is a Kantor double of B ( m , n ) or J is isomorphic to a Cheng–Kac Jordan superalgebra JCK( B ( m ), d ) for some derivation d : B ( m ) → B ( m ).
is not semisimple, then there exist integers m , n and a Jordan bracket { , } on B ( m, n ) such that J = B ( m , n ) + B ( m , n ) v = KJ( B ( m , n ), { , }) is a Kantor double of B ( m , n ) or J is isomorphic to a Cheng–Kac Jordan superalgebra JCK( B ( m ), d ) for some derivation d : B ( m ) → B ( m ).
1.6.4. Non-unital simple Jordan superalgebras
Finally, let us consider non-unital simple Jordan superalgebras. As we have seen, K 3the three-dimensional Kaplansky superalgebra and K 9the nine-dimensional degenerate Kac superalgebra are examples of such superalgebras.
EXAMPLE 1.23.– Let Z be a unital associative commutative algebra, D : Z → Z a derivation. Assume that Z is D -simple and that the only constants are elements α 1, α ∈ F .
Let us consider in Z the bracket { , } given by:

The above bracket is a Jordan bracket, so the Kantor double V ( Z , D ) = Z + Zv = KJ( Z , { , }) is a simple unital Jordan superalgebra.
Now we will change the product in V ( Z , D ), modifying only the action of the even part on the odd part and preserving the product of two even (respectively, two odd) elements. Denote with juxtaposition the product on V ( Z , D ). Let a , b ∈ Z . We define the new product ∙ by:
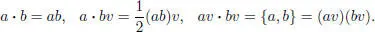
In this way, we get another Jordan superalgebra V 1/2( Z , D ) that is simple but not unital.
It was proved in Zelmanov (2000) that:
THEOREM 1.4.– Let J be a finite dimensional simple central non-unital Jordan superalgebra over a field F . Then J is isomorphic to one of the superalgebras on the list:
1 i) the Kaplansky superalgebra K3 ( example 1.12);
2 ii) the field F has characteristic 3 and J is the degenerate Kac superalgebra ( example 1.15);
3 iii) a superalgebra V1/2(Z, D) ( example 1.23).
DEFINITION 1.14.– Let A be a Jordan superalgebra and let N be its radical, that is, the largest solvable ideal of A. The superalgebra A is said to be semisimple if N = ( 0 ).
EXAMPLE 1.24.– Let B be a simple non-unital Jordan superalgebra and let H ( B ) = B + F 1 be its unital hull. Then H ( B ) is a semisimple Jordan superalgebra that is not simple.
Читать дальше

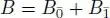 with
with 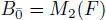 ,
, 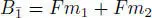 , where F is a field, char F = 3. The product in
, where F is a field, char F = 3. The product in 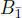 is given by:
is given by: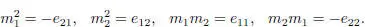
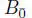 over
over 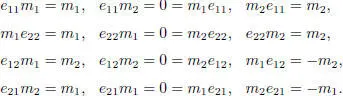
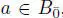 , where a ↦ ā is the symplectic involution, and
, where a ↦ ā is the symplectic involution, and 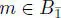 .
.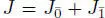 be a finite dimensional central simple Jordan superalgebra over an algebraically closed field F of char F = p > 2. If
be a finite dimensional central simple Jordan superalgebra over an algebraically closed field F of char F = p > 2. If 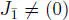 and
and 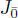 is semisimple, then J is isomorphic to one of the superalgebras in examples 1.8, 1.9, 1.10– 1.14or char F = 3 and J is the nine-dimensional degenerate Kac superalgebra (see example 1.15) or J is isomorphic to one of the superalgebras in examples 1.21and 1.22.
is semisimple, then J is isomorphic to one of the superalgebras in examples 1.8, 1.9, 1.10– 1.14or char F = 3 and J is the nine-dimensional degenerate Kac superalgebra (see example 1.15) or J is isomorphic to one of the superalgebras in examples 1.21and 1.22.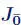 is not semisimple
is not semisimple the algebra of truncated polynomials in m variables. Let B ( m, n ) = B ( m ) ⊗ G ( n ) be the tensor product of B ( m ) with the Grassmann algebra G ( n ) = 〈 1, ξ 1,…, ξn 〉. Then B ( m, n ) is an associative commutative superalgebra.
the algebra of truncated polynomials in m variables. Let B ( m, n ) = B ( m ) ⊗ G ( n ) be the tensor product of B ( m ) with the Grassmann algebra G ( n ) = 〈 1, ξ 1,…, ξn 〉. Then B ( m, n ) is an associative commutative superalgebra.