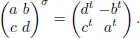
The Lie and Jordan superalgebras (respectively) that consist of skew-symmetric and symmetric elements, respectively, are denoted as P n( F ) and JP n( F ) (and are also called “strange series”).
EXAMPLE 1.12.– The three-dimensional Kaplansky superalgebra K 3= Fe + ( Fx + Fy ) with multiplication table:
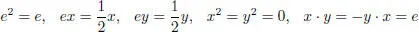
is a simple Jordan superalgebra. Note that K 3is not unital.
EXAMPLE 1.13.– The one-parametric family of four-dimensional superalgebras D ( t ) defined as D ( t ) = ( Fe 1+ Fe 2) + ( Fx + Fy ) with the product
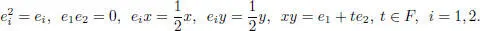
The superalgebra D ( t ) is simple if t ≠ 0 . In the case t = –1, the superalgebra D (–1) is isomorphic to M 1+1( F ) (+).
EXAMPLE 1.14.– Let V be a vector space that is ℤ/2ℤ-graded, 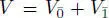 , and has a superform (|) : V × V → F , which is symmetric on
, and has a superform (|) : V × V → F , which is symmetric on 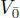 , skew-symmetric in
, skew-symmetric in 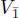 and
and 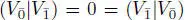 . Then
. Then 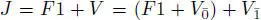 is a Jordan superalgebra, where the product of two arbitrary elements α 1 + v and β 1 + ω in J is given by
is a Jordan superalgebra, where the product of two arbitrary elements α 1 + v and β 1 + ω in J is given by
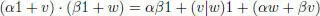
for arbitrary v , ω ∈ V .
We will refer to J as the superalgebra of a superform.
J is simple if and only if the form (|) is non-degenerate.
EXAMPLE 1.15.– Kac (1977a) introduced a 10 -dimensional Jordan superalgebra J whose even part has dimension 6 and splits as the direct sum of a superalgebra of a superform and a one-dimensional algebra. Thus, 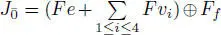 has the multiplication given by:
has the multiplication given by:
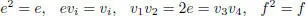
and any other product of two basic elements is 0.
The odd part 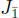 has a basis { x 1, x 2, y 1, y 2} and the following multiplication table:
has a basis { x 1, x 2, y 1, y 2} and the following multiplication table:
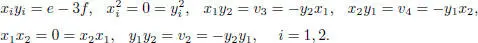
Finally, the action of 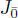 over
over 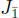 is given by:
is given by:
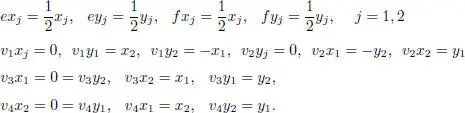
This superalgebra is simple if char F ≠ 3. In case of char F = 3, it has an ideal of dimension 9 that is spanned by e , vi , 1 ≤ i ≤ 4, xj , yj , 1 ≤ j ≤ 2. It is called degenerated Kac superalgebra and is denoted by K 9.
In Medvedev and Zelmanov (1992), it is proved that the Kac superalgebra K 10is not a homomorphic image of a special Jordan superalgebra.
Benkart and Elduque (2002) realized K 10as the space of K 3⊗ K 3+ F 1 (with a new product) where K 3is the Kaplansky superalgebra.
Another (octonionic) construction of K 10was suggested in Racine and Zelmanov (2015).
DEFINITION 1.10.– Let A be an associative commutative superalgebra . A binary map { , } : A × A → A is called a Poisson bracket if
1 1) (A, { , }) is a Lie superalgebra;
2 2) {ab, c} = a{b, c} + (–1)|b||c|{a, c}b for arbitrary .
EXAMPLE 1.16.– Let F [ p 1,…, pn, q 1,…, qn ] be a polynomial algebra in 2 n variables. The classical Hamiltonian bracket:
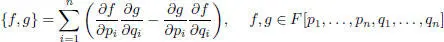
is a Poisson bracket.
EXAMPLE 1.17.– Let
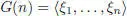
be the Grassmann algebra over an n -dimensional vector space V . Then the bracket
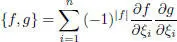
for arbitrary  is a Poisson bracket.
is a Poisson bracket.
DEFINITION 1.11.– Given 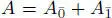 an associative commutative superalgebra , a bilinear map { , } : A × A → A is called a contact bracket if :
an associative commutative superalgebra , a bilinear map { , } : A × A → A is called a contact bracket if :
1 i) (A, { , }) is a Lie superalgebra;
2 ii) {ab, c} = a{b, c} + (–1)|b||c|{a, c}b + abD(c) for arbitrary homogeneous elements a, b, c in A.
Note that a Poisson bracket is a contact bracket with D = 0.
EXAMPLE 1.18.– Let F [ t ] be the polynomial algebra. Then the bracket { f ( t ), g ( t )} = f ′( t ) g ( t ) – f ( t ) g ′( t ) is a contact bracket.
EXAMPLE 1.19.– Let Λ(1 : n ) be the polynomial superalgebra in one (even) Laurent variable and n (odd) Grassmann variables ξ 1,…, ξn , Λ(1 : n ) = F [ t , t –1, ξ 1,…, ξn ]. Consider 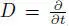 or
or 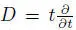 a derivation of F [ t , t –1]. The bilinear map defined on generators of Λ(1 : n ) by:
a derivation of F [ t , t –1]. The bilinear map defined on generators of Λ(1 : n ) by:
Читать дальше

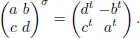
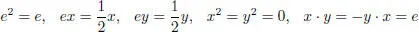
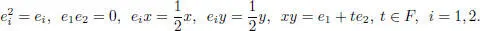
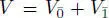 , and has a superform (|) : V × V → F , which is symmetric on
, and has a superform (|) : V × V → F , which is symmetric on 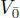 , skew-symmetric in
, skew-symmetric in 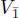 and
and 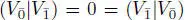 . Then
. Then 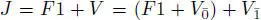 is a Jordan superalgebra, where the product of two arbitrary elements α 1 + v and β 1 + ω in J is given by
is a Jordan superalgebra, where the product of two arbitrary elements α 1 + v and β 1 + ω in J is given by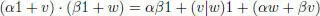
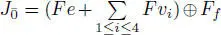 has the multiplication given by:
has the multiplication given by: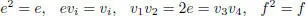
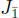 has a basis { x 1, x 2, y 1, y 2} and the following multiplication table:
has a basis { x 1, x 2, y 1, y 2} and the following multiplication table: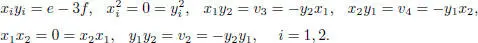
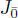 over
over 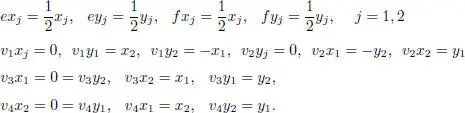
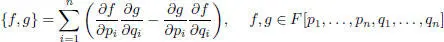
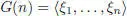
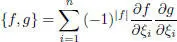
 is a Poisson bracket.
is a Poisson bracket.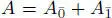 an associative commutative superalgebra , a bilinear map { , } : A × A → A is called a contact bracket if :
an associative commutative superalgebra , a bilinear map { , } : A × A → A is called a contact bracket if :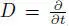 or
or 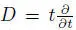 a derivation of F [ t , t –1]. The bilinear map defined on generators of Λ(1 : n ) by:
a derivation of F [ t , t –1]. The bilinear map defined on generators of Λ(1 : n ) by:










