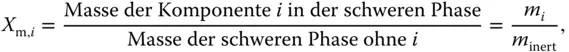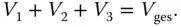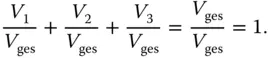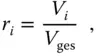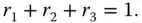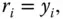Schauen Sie sich jetzt das etwas komisch erscheinende Konzentrationsmaß der Beladung an. Statt Kleinbuchstaben wie beim Stoffmengenanteil ( x , y ) werden hier Großbuchstaben ( X , Y ) zur Bezeichnung der Beladung verwendet. Die Bezeichnung X bezieht sich auch hier auf die schwere Phase, dementsprechend Y auf die leichte Phase. Die Definition der Molbeladung sieht auf den ersten Blick ähnlich aus wie die des Stoffmengenanteils, weist aber einen sehr wichtigen Unterschied auf:
(3.7) 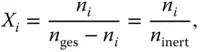
(3.8) 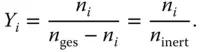
Bezugsgröße bei der Beladung ist nicht die gesamte Stoffmenge n ges, sondern jeweils die Stoffmenge der inerten schweren Phase n inertohne den betrachteten Stoff i (inert bedeutet hier: inert gegenüber Stoff i , da dieser im Nenner nicht berücksichtigt wird). Zur Verdeutlichung können Sie das auch in Prosa formulieren:
(3.9) 
(3.10) 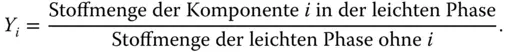
 Für das Beispiel in Abbildung 3.1bedeutet dies für das Schwefeldioxid:
Für das Beispiel in Abbildung 3.1bedeutet dies für das Schwefeldioxid:
(3.11) 
Und jetzt wird es scheinbar ganz komisch! Sie sind es gewohnt, dass Konzentrationsmaße zwischen 0 und 1 laufen, siehe Formel 3.6für Massen- und Stoffmengenanteile. Da Sie die Beladung auf den inerten Anteil beziehen, kann die Beladung im Gegensatz zu den Stoffmengenanteilen Werte zwischen null, kein Stoff i vorhanden, und unendlich, die Phase besteht nur aus dem Stoff i , annehmen:
(3.12) 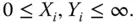
 Abbildung 3.3zeigt eine gasförmige und eine flüssige Mischphase. Die Übergangskomponente geht von der Gas- in die Flüssigphase über. Stellen Sie sich die Übergangskomponente wieder als SO 2vor. Die Beladung der Übergangskomponente (Komponente i ) wird auf die reine Flüssigkeit
Abbildung 3.3zeigt eine gasförmige und eine flüssige Mischphase. Die Übergangskomponente geht von der Gas- in die Flüssigphase über. Stellen Sie sich die Übergangskomponente wieder als SO 2vor. Die Beladung der Übergangskomponente (Komponente i ) wird auf die reine Flüssigkeit

bezogen. Mit n wird hier wieder die Stoffmenge in mol bezeichnet. Für die Gasphase gilt entsprechend:
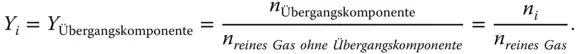
Die Stoffmengenanteile x
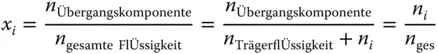
beziehungsweise y
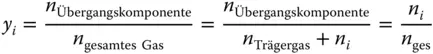
werden im Gegensatz zur Beladung auf die gesamte Stoffmenge n gesbezogen.
Schauen Sie sich die Gasphase an: sowohl der Stoffmengenanteil y als auch die Beladung Y werden zu null, wenn sich keine Übergangskomponente im Gas befindet. Besteht das Gas dagegen nur aus Übergangskomponente, wird der Stoffmengenanteil zu eins 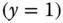 , die Beladung aber unendlich groß
, die Beladung aber unendlich groß 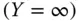 . Das gleiche gilt für die flüssige Phase.
. Das gleiche gilt für die flüssige Phase.
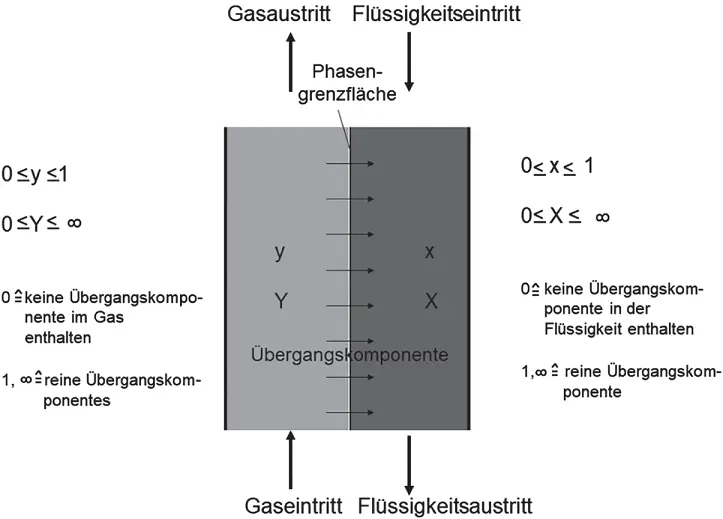
Abbildung 3.3Stoffmengenanteile und Beladungen am Beispiel des Stoffübergangs von der gasförmigen zur flüssigen Phase
Die Beladung kann auch als Massenbeladung
(3.13) 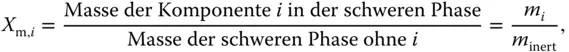
(3.14) 
angegeben werden.
Abbildung 3.4zeigt 3 unterschiedliche Behälter, in denen sich die drei Gase 1, 2 und 3 befinden. Druck p und Temperatur T sind in jedem Behälter identisch, die Massen ( m 1, m 2, m 3) und Volumina ( V 1, V 2, V 3) unterscheiden sich allerdings. Die drei Gase werden bei gleichem Druck und gleicher Temperatur in einem Behälter zusammengeführt (Behälter 4). Für diesen Behälter gilt bei diesen Randbedingungen, wenn die Massen der Gase unverändert bleiben:
(3.15) 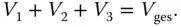
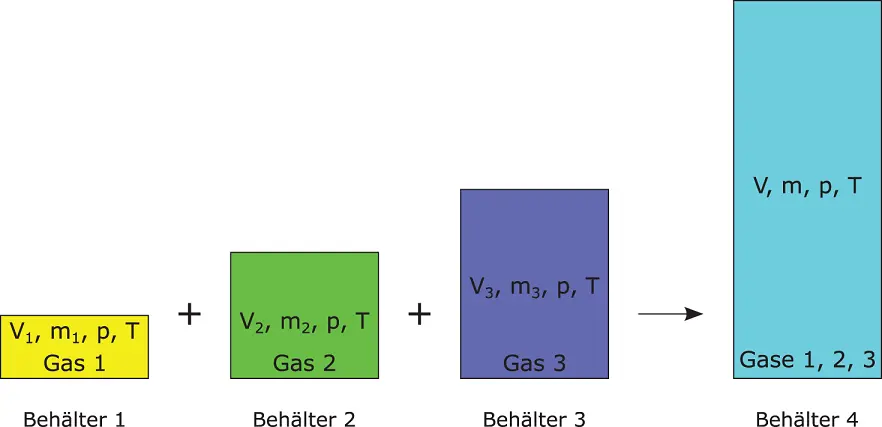
Abbildung 3.4Volumenanteil
Das Volumen von Behälter 4 muss genauso groß sein wie die Volumina der 3 anderen Behälter zusammen. Wenn Sie durch das Gesamtvolumen V gesdividieren, erhalten Sie
(3.16) 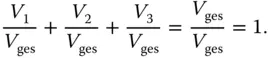
Mit der Definition des Volumenanteils r ider Komponente i
(3.17) 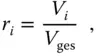
ergibt sich
(3.18) 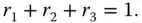
Der Volumenanteil läuft wie der Mol- und Massenanteil zwischen den Grenzen 0 und 1. Für ideale Gase ist der Volumenanteil gleich dem Stoffmengenanteil:
(3.19) 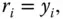
Читать дальше

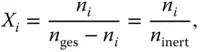
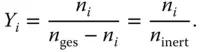

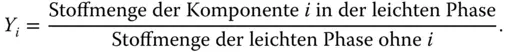
 Für das Beispiel in Abbildung 3.1bedeutet dies für das Schwefeldioxid:
Für das Beispiel in Abbildung 3.1bedeutet dies für das Schwefeldioxid:
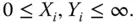

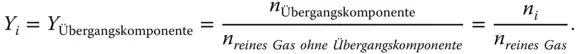
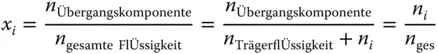
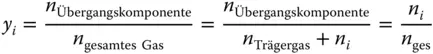
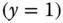 , die Beladung aber unendlich groß
, die Beladung aber unendlich groß 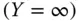 . Das gleiche gilt für die flüssige Phase.
. Das gleiche gilt für die flüssige Phase.