Jules Verne - Reise um den Mond

»Ah! Mein Gott, was seid ihr für Buchstabenfresser! Ihr glaubt, mit eurer Algebra alles fertig bringen zu können.«

»Michel«, entgegnete Barbicane, »meinst du, man könne ohne Hammer schmieden oder ohne Pflug ein Feld bestellen?«

»Schwerlich.«

»Also! Die Algebra ist ein Werkzeug wie ein Pflug oder ein Hammer, und für den, welcher sich damit auskennt, ein vortreffliches Werkzeug.«

»Ach, im Ernst?«

»Ja, das ist sehr ernst gemeint!«

»Und du könntest in meiner Gegenwart von diesem Werkzeug Gebrauch machen?«

»Wenn es dich interessiert?«

»Und mir zeigen, wie man die Anfangsgeschwindigkeit unseres Projektils ausgerechnet hat?«

»Ja, mein werter Freund. Indem ich alle Elemente des Problems berücksichtige: die Entfernung des Zentrums der Erde von dem des Mondes, den halben Durchmesser der Erde, die Erdmasse und die Mondmasse. Anhand dieser Elemente kann ich ganz genau berechnen, wie groß die Anfangsgeschwindigkeit des Projektils sein musste, und zwar mithilfe einer simplen Formel.«

»Lass hören! Welche Formel?«

»Du sollst sie zu hören bekommen. Nur werde ich dir nicht die krummen Linien bezeichnen, welche das Projektil zwischen der Erde und dem Mond beschreibt, indem ich ihre Bewegung um die Sonne mit in die Rechnung einbeziehe. Sondern ich will die beiden Gestirne als unbewegt voraussetzen, das reicht für unseren Zweck aus.«

»Und weshalb?«

»Weil ich sonst die Lösung der Aufgabe suchen würde, die man das Problem der drei Körper nennt, wozu die Integralrechnung noch nicht weit genug ausgereift ist.«

»Demnach«, sagte Michel Ardan in spöttischem Ton, »haben die Mathematiker noch nicht ihr letztes Wort gesprochen?«

»Allerdings nicht«, erwiderte Barbicane.

»Gut! Vielleicht sind die Seleniten in der Integralrechnung etwas weitergekommen! Und nebenbei: Was bezeichnet man denn als Integralrechnung?«

»Diese Rechenart ist das Gegenteil von der Differentialrechnung«, erklärte Barbicane mit würdigem Ernst.

»Danke verbindlichst.«

»Mit anderen Worten, es handelt sich um eine Rechenart, mit der man die bestimmten Größen sucht, deren Differentiale man kennt.«

»Das ist wenigstens deutlich ausgesprochen«, erwiderte Michel mit der zufriedensten Miene.

»Und nun«, fuhr Barbicane fort, »gebt mir ein Stückchen Papier und einen Bleistift. Und vor Ablauf einer halben Stunde will ich die gewünschte Formel gefunden haben.«

Darauf vertiefte sich Barbicane in seine Arbeit, während Nicholl in den Weltraum hinaussah und es seinen Kameraden überließ, für das Frühstück zu sorgen. Noch bevor eine halbe Stunde vergangen war, hob Barbicane den Kopf und zeigte Michel eine ganze Seite voll mit algebraischen Zeichen, darunter auch die gesuchte, allgemeine Formel:

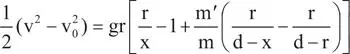
»Und was bedeutet das ... ?«, fragte Michel.

»Es bedeutet«, erklärte Nicholl, »ein halb v zum Quadrat minus v Null zum Quadrat ist gleich gr multipliziert mit r durch x minus 1 plus m‘ geteilt durch m, multipliziert mit r durch d minus x, minus r durch d minus r ...«

»X auf y steigt auf z und reitet über p«, rief Michel Ardan mit hellem Lachen. »Und das begreifst du, Kapitän?«

»Nichts leichter als das.«

»Wieso?«, fragte Michel. »Aber das ist doch einleuchtend und mehr wollte ich gar nicht.«

»Immer nur lachen!«, versetzte Barbicane. »Du wolltest Algebra und nun hast du sie, voll und ganz!«

»Lieber lasse ich mich hängen!«

»Tatsächlich!«, mischte sich Nicholl ein, der als Experte die Formel prüfte. »Es scheint mir richtig abgeleitet, Barbicane. Es ist die Integrale der Gleichung faktischer Kräfte, und ich habe keinen Zweifel daran, dass sie uns das gesuchte Ergebnis liefern wird.«

»Aber ich möchte es auch verstehen!«, rief Michel. »Ich würde Nicholl zehn Jahre meines Lebens dafür geben!«

»So höre denn, Michel«, fuhr Barbicane fort. »Ein halb v zum Quadrat minus v Null zum Quadrat ist die Formel, welche uns die ›halbe‹ Veränderung der faktischen Kraft erklärt.«

»Gut. Und Nicholl weiß, was das bedeutet?«

»Allerdings, Michel«, antwortete der Kapitän. »Alle diese Zeichen, welche dir wie eine Geheimsprache vorkommen, bilden für den, der sie versteht, die klarste, deutlichste, logischste Sprache.«

»Nicholl, und du behauptest also«, fragte Michel, »dass du mithilfe dieser Hieroglyphen, die noch unverständlicher aussehen, als die des ägyptischen Ibisses, herausfinden könntest, welche Anfangsgeschwindigkeit man dem Projektil geben musste?«

»Unbestreitbar«, erwiderte Nicholl. »Und ich werde dir mithilfe derselben Formel zu jedem Zeitpunkt angeben können, wie groß seine Geschwindigkeit auf jedem Punkt seiner Fahrt ist.«

»Dein Wort darauf?«

»Mein Wort darauf.«

»Dann bist du ein Rechenkünstler wie unser Präsident?«

»Nein, Michel. Barbicane hat etwas Schwieriges geleistet, indem er eine Gleichung aufstellte, die sämtliche Bedingungen des Problems berücksichtigt. Das übrige ist nur eine Rechenaufgabe, wofür man nur die vier Elemente zu kennen braucht.«

»Das will schon etwas heißen!«, erwiderte Ardan, der in seinem Leben noch keine Additionsaufgabe richtig ausgerechnet hatte und diese Formel folgendermaßen definierte: »Eine Kopf zerbrechende Arbeit aus China, mit der man eine Unzahl an verschiedenen Summen herausbekommt.«

Barbicane jedoch versicherte, dass Nicholl, wenn er eine Zeit lang darüber nachgesonnen hätte, sicherlich auch zu dieser Formel gekommen wäre.

»Das glaube ich nicht«, sagte Nicholl. »Denn je mehr ich darüber nachdenke, desto mehr erkenne ich ihre Brillanz.«

»Und jetzt pass auf«, sagte Barbicane zu seinem unwissenden Kameraden, »und du wirst sehen, dass alle diese Buchstaben ihre Bedeutung aufweisen.«

»Ich gebe Acht«, sagte Michel mit scheinbarer Resignation.

»d«, sagte Barbicane, »bedeutet die Entfernung des Zentrums der Erde vom Zentrum des Mondes. Denn will man die Anziehungskräfte berechnen, so muss man die Zentren berücksichtigen.«

»Ich verstehe.«

»r bezeichnet den Radius der Erde.«

»r wie Radius. Einzusehen.«

»Mit m wird die Masse der Erde ausgedrückt; m‘ ist die Masse des Mondes. Ganz offensichtlich muss man die Massen der beiden sich anziehenden Planeten in die Berechnung mit einbeziehen, weil die Anziehungskräfte im Verhältnis zu den Massen stehen.«

»Nachvollziehbar.«

»g steht für Gravitations- oder Schwerkraft, das ist die Geschwindigkeit eines auf die Erdoberfläche fallenden Körpers innerhalb einer Sekunde. Ist das verständlich?«

»Wasser aus einem Felsen!«, erwiderte Michel.

»Mit x bezeichne ich die veränderliche Distanz des Projektils vom Zentrum der Erde und mit v die Geschwindigkeit des Projektils bei dieser Distanz.«

»Gut.«

»Mit v Null, wie es in der Gleichung steht, benenne ich die Geschwindigkeit, die das Projektil aufweist, wenn es die Atmosphäre verlässt. Es ist nämlich so, dass man diese Geschwindigkeit genau für diesen Punkt berechnen muss, da wir bereits wissen, dass die Geschwindigkeit beim Abschuss genau zwei Dritteln von der Geschwindigkeit entspricht, die das Projektil beim Austritt aus der Atmosphäre hat.«

»Mach nur weiter, ich verstehe!«, sagte Michel.

»Siehst du, es ist doch ganz einfach«, erwiderte Barbicane.

»Aber nicht für mich«, entgegnete Michel.

»Das will also heißen: Als unser Projektil an der Grenze zur Erdatmosphäre angekommen war, hatte es schon ein Drittel seiner Anfangsgeschwindigkeit verloren.«

»So viel?«

»Ja, mein Freund. Und das lediglich aufgrund der Reibung an den Schichten der Atmosphäre. Du kannst dir sicher vorstellen, dass, je schneller es dahin glitt, umso größer der Widerstand der Luft gewesen war.«