3.2.1.1 Dispersion Effect: Group Velocity Dispersion
When dealing with optical pulses with femtosecond pulse durations, it is important to consider the effects of group velocity dispersion (GVD). The latter affects the duration of a light pulse which traverses any media, because of the frequency dependence of the refractive index n ( ω ). GVD is defined as:
(3.1) 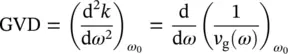
where v gis the group velocity. The latter can be written as:
(3.2) 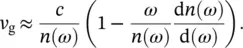
GVD is measured in fs 2mm −1and, in a transparent region, is typically positive because of the characteristic dependence of n on frequency. During propagation, every spectral component of the pulse acquires a different delay, resulting in a temporal broadening of the pulse without any spectral changes [21]. To visualize the effect of GVD on a Gaussian pulse passing through a medium, a simulation is shown in Figure 3.1. From top to bottom, three pulses are shown, representing a transform‐limited Gaussian with FWHM = 5 fs centered at 550 nm, and the same pulse after passing through 1 or 2 mm SiO 2, respectively. As evident from the figure, GVD substantially enlarges the pulse duration, increasing it to several hundreds of femtoseconds. The pulse duration Δ t , that is the FWHM of the Gaussian intensity profile, broadens to Δ t bgiven by:
(3.3) 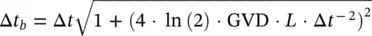
where L is the propagation length inside the material [19]. Besides broadening, GVD causes a frequency chirp , that is a time dependence of the instantaneous frequency of the pulse, given by 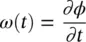 . In Figure 3.1, the chirp is evident from the comparison of the frequencies of the two sides of the pulse, showing that the instantaneous frequency is redder in the front part of the pulse and bluer in the back [19, 20], which is exactly the effect of a positive GVD. In particular, the instantaneous frequency acquires an approximately linear time dependence, ω ( t ) = ω 0+ αt , because the phase of the wave acquires a quadratic time term.
. In Figure 3.1, the chirp is evident from the comparison of the frequencies of the two sides of the pulse, showing that the instantaneous frequency is redder in the front part of the pulse and bluer in the back [19, 20], which is exactly the effect of a positive GVD. In particular, the instantaneous frequency acquires an approximately linear time dependence, ω ( t ) = ω 0+ αt , because the phase of the wave acquires a quadratic time term.
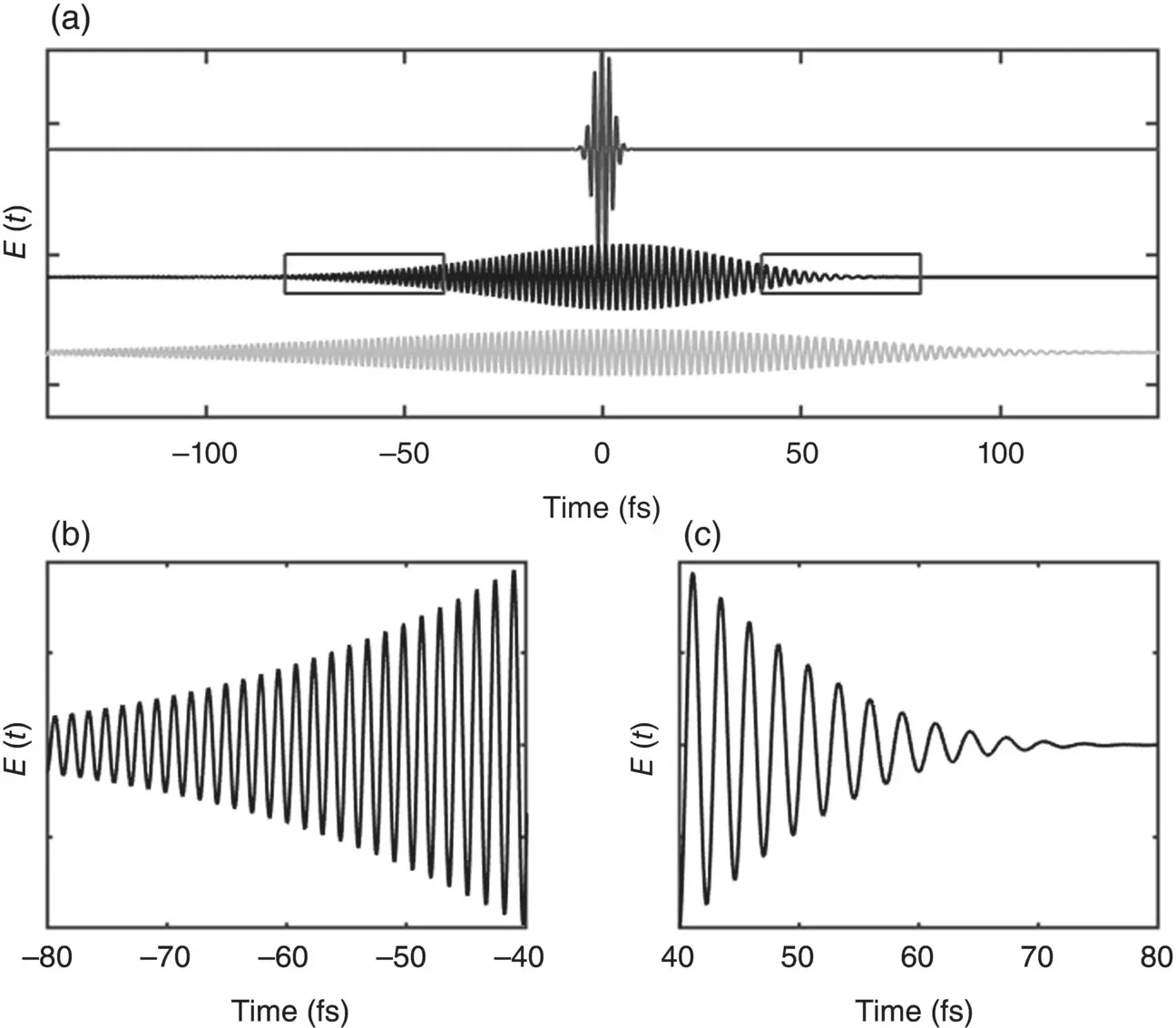
Figure 3.1Panel (a): Simulation of a gaussian pulse centered at 550 nm with FHWM = 5 fs (first curve from the top) after propagation through a SiO 2medium of 1 mm thickness (second curve) and 2 mm (third curve). Panel (b and c): zooms of the tails of the black pulse (squares). Each wavelength is delayed by a different phase, resulting in a longer pulse with a positive chirp (the redder frequencies are faster than the bluer).
Pulse broadening and chirp acquired by femtosecond pulses during their propagation in optical setups need to be put under control in order to preserve good time resolution. One way to do it is to limit the use of transparent optical components, preferring the use of reflective optics only. Some special methods exist to manipulate the chirp, such as what is called a pulse compressor, built by using a pair of prisms or gratings. In a pulse compressor, one can add negative GVD (redder part of a pulse propagates slower than the blue part) which compensates the effect of pulse broadening in a transparent media, recompressing the pulse [19, 20].
Last but not least, dispersion also affects the temporal overlap of two pulses centered at different wavelengths which pass through the same medium, because their group velocities are generally different: this effect is called group velocity mismatch , or GVM. Thereby, if the pulses are initially overlapping in time at a certain point in space, they overlap no more after some propagation distance within a dispersive medium. The GVM effect, for example, can be very important in the generation of pulses through nonlinear effects because it can limit the effective interaction length between the two pulses.
3.2.2 Nonlinear Optics: Basis and Applications
3.2.2.1 Second Harmonic Generation and Sum Frequency Generation
Second harmonic generation (SHG) is a nonlinear optical phenomenon in which two photons of the same frequency, interacting in a nonlinear material, are converted in a single photon with doubled frequency [22]. The polarization 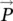 of a medium excited by an electrical field
of a medium excited by an electrical field 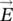 can be expressed as [19, 20]:
can be expressed as [19, 20]:
(3.4) 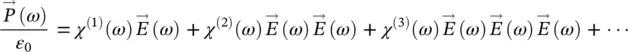
where, in general, χ (n)is a tensor. The first term of the equation describes the phenomena usually encountered in linear optics, while the other describes nonlinear effects at different orders in the electric field. Under certain conditions ( χ (2)≠ 0, as generally occurs in a non‐centrosymmetrical medium), two photons at the same frequency ω 1, passing through an appropriate medium, are combined to generate a new photon with a doubled frequency (2 ω 1). The process follows the laws of energy ( ω 1+ ω 1= 2 ω 1) and momentum conservation ( 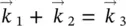 ) and in not‐depleted pump condition (that is, negligible pump absorption) it is possible to describe the intensity of the new beam as [19, 20]:
) and in not‐depleted pump condition (that is, negligible pump absorption) it is possible to describe the intensity of the new beam as [19, 20]:
(3.5) 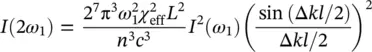
where n is the refractive index, L is the optical path within the nonlinear material, Δ k = k 2− 2 k 1is the so‐called phase mismatch, and χ effis the effective susceptibility which is a certain combination of the components of the χ (2)tensor, which depends on the material and on its orientation. The intensity of the new beam depends on the square of the incident beam intensity, on the length L (with a quadratic dependence if Δ k = 0), and on the degree of phase mismatch. Fulfilling the condition Δ k = 0, named phase matching , gives maximally efficient SHG, and corresponds to the conservation of momentum in the process. It can be seen as a situation in which first and second harmonic beams propagate in the medium with the same speed. In order to achieve this, the refractive index at ω and 2 ω has to be the same. Although this is not generally possible in isotropic media, such a limitation can be overcome by using (uniaxial) birefringent media such as beta‐barium borate (BBO). The latter display two different refractive indexes, ordinary ( n o), and extraordinary ( n e), for beams with two orthogonal polarizations, where the extraordinary index also depends on the angle θ between the 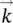 of the beam and the optical axis of the crystal. Thus, one can achieve phase matching, for example, if the beam at ω propagates as an ordinary beam, while the beam at 2 ω propagates as an extraordinary beam. Then, changing the orientation of the crystal, it is possible to find an angle θ for which n e(2 ω , θ ) = n o( ω ), fulfilling the phase matching condition.
of the beam and the optical axis of the crystal. Thus, one can achieve phase matching, for example, if the beam at ω propagates as an ordinary beam, while the beam at 2 ω propagates as an extraordinary beam. Then, changing the orientation of the crystal, it is possible to find an angle θ for which n e(2 ω , θ ) = n o( ω ), fulfilling the phase matching condition.
Читать дальше

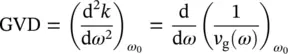
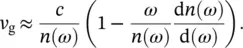
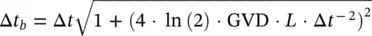
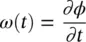 . In Figure 3.1, the chirp is evident from the comparison of the frequencies of the two sides of the pulse, showing that the instantaneous frequency is redder in the front part of the pulse and bluer in the back [19, 20], which is exactly the effect of a positive GVD. In particular, the instantaneous frequency acquires an approximately linear time dependence, ω ( t ) = ω 0+ αt , because the phase of the wave acquires a quadratic time term.
. In Figure 3.1, the chirp is evident from the comparison of the frequencies of the two sides of the pulse, showing that the instantaneous frequency is redder in the front part of the pulse and bluer in the back [19, 20], which is exactly the effect of a positive GVD. In particular, the instantaneous frequency acquires an approximately linear time dependence, ω ( t ) = ω 0+ αt , because the phase of the wave acquires a quadratic time term.
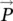 of a medium excited by an electrical field
of a medium excited by an electrical field 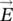 can be expressed as [19, 20]:
can be expressed as [19, 20]: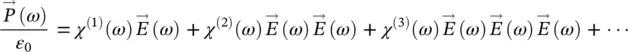
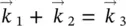 ) and in not‐depleted pump condition (that is, negligible pump absorption) it is possible to describe the intensity of the new beam as [19, 20]:
) and in not‐depleted pump condition (that is, negligible pump absorption) it is possible to describe the intensity of the new beam as [19, 20]: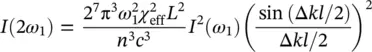
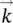 of the beam and the optical axis of the crystal. Thus, one can achieve phase matching, for example, if the beam at ω propagates as an ordinary beam, while the beam at 2 ω propagates as an extraordinary beam. Then, changing the orientation of the crystal, it is possible to find an angle θ for which n e(2 ω , θ ) = n o( ω ), fulfilling the phase matching condition.
of the beam and the optical axis of the crystal. Thus, one can achieve phase matching, for example, if the beam at ω propagates as an ordinary beam, while the beam at 2 ω propagates as an extraordinary beam. Then, changing the orientation of the crystal, it is possible to find an angle θ for which n e(2 ω , θ ) = n o( ω ), fulfilling the phase matching condition.










