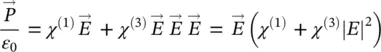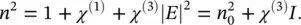Because femtosecond pulses are intrinsically broadband, another important parameter in SHG is the extent of spectral bandwidth which is effectively doubled (acceptance bandwidth), not necessarily coincident with the whole pulse bandwidth. In fact, the phase matching condition is exactly fulfilled only at a given wavelength, and therefore it cannot be exactly fulfilled across the entire pulse bandwidth. In practice, assuming that the first harmonic beam at λ 1propagates as an ordinary beam, and a SHG beam is produced as an extraordinary beam at λ 2= λ 1/2, the portion d λ 1of the doubled pulse bandwidth is given by [23]:
(3.6) 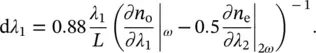
Therefore, to increase the bandwidth of the doubled beam, it is necessary to decrease the crystal thickness L , at the cost of SHG efficiency (proportional to L 2). Therefore, according to the experimental requirements, one needs to find the right compromise between the two needs.
SHG is a specific nonlinear process which involves two photons with the same energy. Other second‐order nonlinear processes are possible, such as sum and difference frequency generation (SFG and DFG), where two photons with different energies combine together into a third photon. As for SHG, these processes need to satisfy energy and momentum conservation, which for SFG are expressed by: ω 3= ω 1+ ω 2and 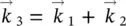 (equations for DFG have a minus sign). Also here, phase matching can be achieved within a birefringent nonlinear crystal. As compared to the efficiency equation reported in Eq. (3.5), the intensity of the pulse obtained by SFG or DFG depends on the product of the two incoming intensities (
(equations for DFG have a minus sign). Also here, phase matching can be achieved within a birefringent nonlinear crystal. As compared to the efficiency equation reported in Eq. (3.5), the intensity of the pulse obtained by SFG or DFG depends on the product of the two incoming intensities ( 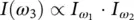 ) [24].
) [24].
3.2.2.2 Noncollinear Optical Parametric Amplifier
A noncollinear optical parametric amplifier (NOPA) is an optical device capable of producing tunable femtosecond radiation in the visible or near‐infrared region. The output of a NOPA is obtained by the interaction of two beams in a nonlinear crystal: a strong pump ( ω p) and a weak and broadband seed ( ω s< ω p). The pump is used to amplify the seed intensity, producing a strong output beam, named the signal , while creating another beam named idler at ω i, where ω p= ω s+ ω ifor energy conservation. In practice, the nonlinear process involved can be seen as difference frequency generation (DFG) between the pump and the seed. If the pump is the second harmonic at 400 nm of the Ti:sapphire beam, ω ifalls in the infrared region, and the output signal wavelength can be typically tuned from 490 to 760 nm. Considering that the seed is a broadband pulse, changing the orientation of the nonlinear crystal allows to amplify different wavelengths based on the particular phase matching condition fulfilled in a given orientation [25].
Optical parametric amplification can be obtained either in a collinear or noncollinear geometry. The NOPA configuration uses the latter, allowing to compensate for the group velocity mismatch (GVM) between the two pulses ( Figure 3.2a), which limits the interaction length and, therefore, the amplification of the seed into the signal.
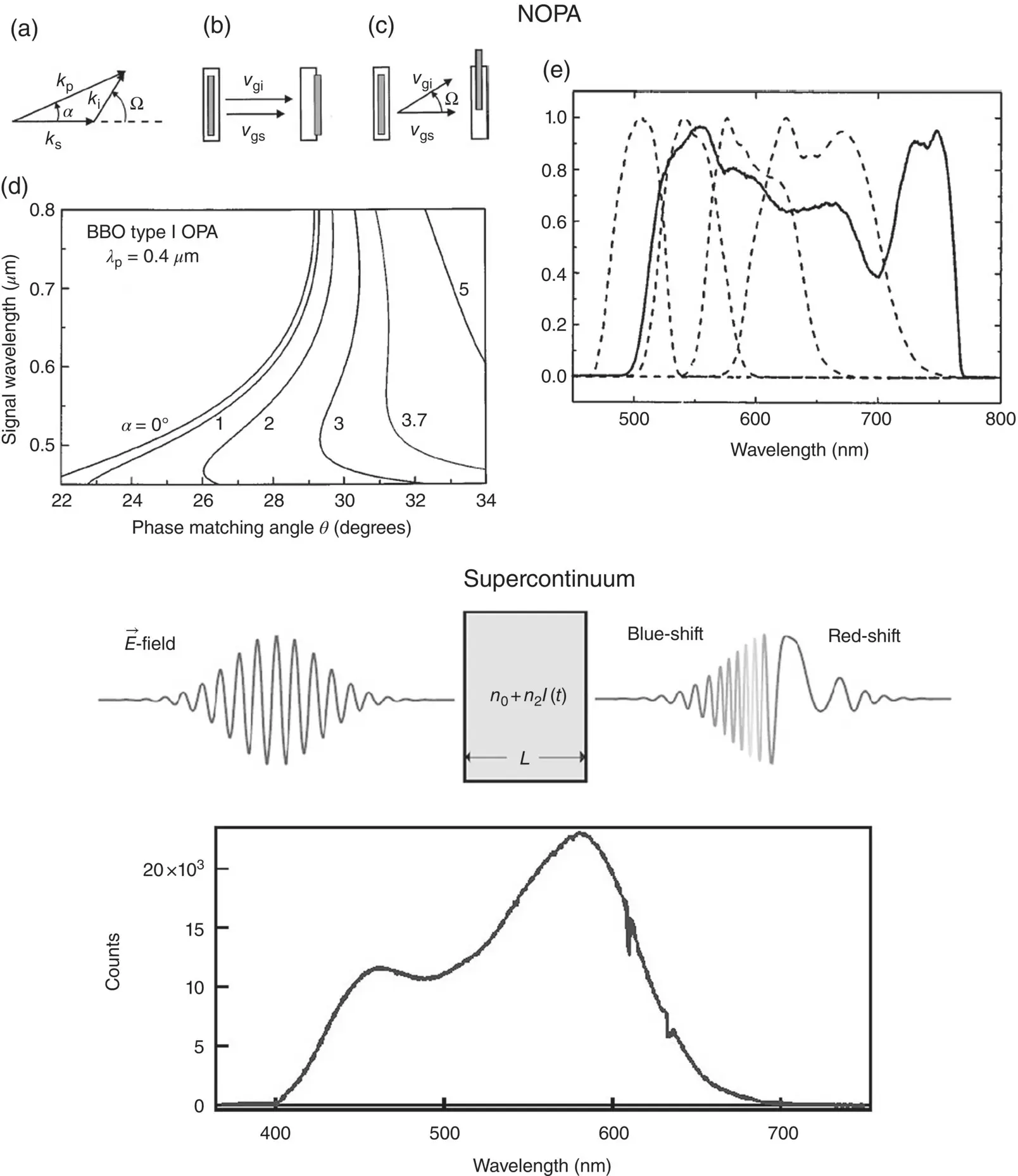
Figure 3.2Top: (a) Wavevectors of pump ( 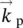 ), signal (
), signal ( 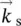 ), and idler (
), and idler ( 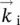 ) in the NOPA geometry; (b) group velocity mismatch of signal and idler pulses in collinear geometry and (c) in noncollinear geometry. The interaction length between the pulses is longer in (c) than in (b). (d) Phase matching curves for a NOPA pumped at 400 nm, as a function of the pump‐signal angle. (e) Solid curve: NOPA spectrum under optimum alignment conditions and a compressed seed; dashed line: sequence of spectra obtained by changing the white light chirp.
) in the NOPA geometry; (b) group velocity mismatch of signal and idler pulses in collinear geometry and (c) in noncollinear geometry. The interaction length between the pulses is longer in (c) than in (b). (d) Phase matching curves for a NOPA pumped at 400 nm, as a function of the pump‐signal angle. (e) Solid curve: NOPA spectrum under optimum alignment conditions and a compressed seed; dashed line: sequence of spectra obtained by changing the white light chirp.
Source: Reprinted from [25], with the permission of AIP Publishing.
Bottom: Generation of supercontinuum pulse (white light) from a red pulse propagating in a centrosymmetric medium and supercontinuum spectrum generated by 800 nm beam pulse focused in a 2 mm D 2O quartz cell filtered by a short‐pass filter at 750 nm.
The advantages of a noncollinear configuration can be also explained in different terms. In a noncollinear configuration, the crystal orientation angle at which phase matching occurs for amplification of a given wavelength becomes dependent on the angle α between the pump and signal wavevectors propagating inside the crystal, as in Figure 3.2d. In particular, as demonstrated in Figure 3.2e, the phase matching condition is simultaneously achieved over a very broad wavelength range when α ∼ 3.7 ∘. This allows to produce very broadband output pulses, which can be then compressed to very short temporal durations even below 10 fs. Usually, the output pulse is not broad as the near‐vertical line in Figure 3.2e because the seed is temporally chirped and the interaction with the pump only involves a relatively narrow portion of the seed spectrum. Then, changing the alignment (spatially and temporally) between pump and signal allows to amplify different portions of the spectrum, as shown by the dashed lines in Figure 3.2e.
3.2.2.3 Supercontinuum Generation
The weak seed of a NOPA, usually, is a spectrally broad ultrashort light pulse. These pulses are called white light or supercontinuum pulses [26] and are generated by a third‐order nonlinear phenomenon named self‐phase modulation (SPM), combined to another phenomenon called self‐focusing (SF). Besides the NOPA seed, these white light pulses are also used as probe pulses for transient absorption experiments discussed in the next section. To understand the generation of these supercontinuum pulses, consider a centrosymmetric material such as a liquid or glass ( χ (2)= 0). Taking into account third‐order nonlinear effects, the instantaneous polarization can be written as:
(3.7) 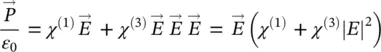
which makes it possible to write the square of the refractive index n as:
(3.8) 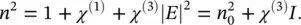
Therefore, a propagating pulse will produce a change of the refractive index related to its instantaneous intensity. Considering the temporal and spatial distribution of the pulse intensity, and considering that χ (3)is usually very small, the last expression is usually approximated in first order as n ≈ n 0+ n 2 I ( r , t ), where the nonlinear refractive index n 2is closely related to χ (3). Considering a Gaussian beam, the intensity depends on position and time. Therefore, one may expect both spatial and temporal changes of the refractive index, which give rise, respectively, to SF and SPM [26].
Читать дальше

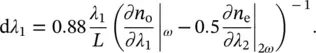
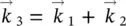 (equations for DFG have a minus sign). Also here, phase matching can be achieved within a birefringent nonlinear crystal. As compared to the efficiency equation reported in Eq. (3.5), the intensity of the pulse obtained by SFG or DFG depends on the product of the two incoming intensities (
(equations for DFG have a minus sign). Also here, phase matching can be achieved within a birefringent nonlinear crystal. As compared to the efficiency equation reported in Eq. (3.5), the intensity of the pulse obtained by SFG or DFG depends on the product of the two incoming intensities ( 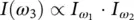 ) [24].
) [24].
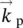 ), signal (
), signal ( 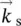 ), and idler (
), and idler ( 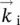 ) in the NOPA geometry; (b) group velocity mismatch of signal and idler pulses in collinear geometry and (c) in noncollinear geometry. The interaction length between the pulses is longer in (c) than in (b). (d) Phase matching curves for a NOPA pumped at 400 nm, as a function of the pump‐signal angle. (e) Solid curve: NOPA spectrum under optimum alignment conditions and a compressed seed; dashed line: sequence of spectra obtained by changing the white light chirp.
) in the NOPA geometry; (b) group velocity mismatch of signal and idler pulses in collinear geometry and (c) in noncollinear geometry. The interaction length between the pulses is longer in (c) than in (b). (d) Phase matching curves for a NOPA pumped at 400 nm, as a function of the pump‐signal angle. (e) Solid curve: NOPA spectrum under optimum alignment conditions and a compressed seed; dashed line: sequence of spectra obtained by changing the white light chirp.