2.2 Zahlen, Ziffern und Werte: Grundbegriffe
„Ich bin jetzt seit 34 Jahren Trainer, da habe ich gelernt, dass zwei und zwei niemals vier ist.“
Leon Beenhakker
Der Inhalt von Datentabellen besteht überwiegend aus Zahlen, Ziffern und Werten.
Zahlen
Die Menge der Zahlen wird, vereinfacht ausgedrückt, in Ganzzahlen und Bruchzahlen unterteilt. Ganz- und Bruchzahlen können jeweils als Quotienten Q = p / q (wobei p und q Ganzzahlen, und q ≠ 0) ausgedrückt werden. Der Unterschied zwischen Ganzzahlen und Bruchzahlen wird i. Allg. anhand zweier Aspekte beschreiben:
■ Der Quotient Q von Ganzzahlen besitzt keinen Rest, hat also keine Nachkommastellen. Der Quotient Q von Bruchzahlen hat dagegen einen Rest.
■ Von Bruchzahlen wird gesagt, dass sie nicht in der Natur vorkommen. Ganzzahlen werden daher auch als „natürliche“ Zahlen bezeichnet.
Ganzzahl
Die ganzen Zahlen (Quotienten ohne Nachkommastellen) umfassen alle Zahlen: …, -3, -2, -1, 0, 1, 2, 3, … Alternative Bezeichnungen für Ganzzahl sind „Natürliche Zahl“, „Zählzahl“ oder „Integer“.
| Menge |
Bezeichnung |
| …, -3, -2, -1, 0, 1, 2, 3, … |
Ganzzahlen |
| 1, 2, 3, … |
Positive Ganzzahlen |
| …, -3, -2, -1 |
Negative Ganzzahlen |
| 0, 1, 2, 3, … |
Nonnegative Ganzzahlen |
| …, -3, -2, -1, 0 |
Nonpositive Ganzzahlen |
Ganze Zahlen sind eindeutig geordnet. Ganze Zahlen können dadurch eindeutig untereinander verglichen werden. Der Wert 0 weist dabei mehrere Besonderheiten auf. 0 ist die einzige Ganzzahl, die weder positiv noch negativ ist. Gemäß dieser Auffassung ist 0 ein Element der Ganzzahlen; Einigkeit besteht in diesem Punkt in der Mathematik jedoch nicht. Als Zählwert bedeutet 0, dass keine Elemente (z.B. innerhalb einer Menge) vorhanden sind. Eine Zahl, die daher ungleich 0 ist, wird daher auch als non-null bezeichnet. Ein 0 kann zugleich nonpositiv wie auch nonnegativ sein (s.u.).
Die oben wiedergegebene Abschlusstabelle der Bundesligasaison 2011/2012 enthält ausschließlich Ganzzahlen als Daten. Die obigen Ausführungen sollten ausreichen, den Typ der dargestellten Ganzzahlen interpretieren zu können. Die Spalte „Platz“ ist z.B. eine positive Ganzzahl; es gibt theoretisch keinen Platz 0 (einen negativen Wert gibt es in dieser Spalte ebenfalls nicht). Vergleichbar sieht es bei der Spalte „Spiele“ aus; am letzten Spieltag scheint „Spiele“ eine positive Ganzzahl zu sein. Betrachtet man jedoch den ersten Spieltag, ändert sich die Sichtweise: Werden Spiele, wie in der Bundesliga meist üblich, auf Freitag, Samstag und Sonntag verteilt, so steht bei manchen Mannschaften bis zum letzten Spiel unter „Spiele“ der Wert 0. Die Spalte „Spiele“ ist z.B. eine nonnegative Ganzzahl; es gibt theoretisch einen Platz 0 (einen negativen Wert gibt es in dieser Spalte nicht). Dasselbe gilt für die Spalten „S“, „U“, und „N“ (jeweils für Sieg, Unentschieden oder Niederlage): Mannschaften können (zumindest für eine Weile) keine Siege, Unentschieden oder auch Niederlagen erleben. Die Spalte „Tore“ enthält, von einem Doppelpunkt getrennt, die Anzahl der geschossenen bzw. kassierten Tore. Wir überspringen der Einfachheit halber diese Spalte und schauen uns die abgeleitete Spalte „Diff“ an, die Differenz aus den geschossenen bzw. kassierten Toren. Die Abschlusstabelle der Bundesligasaison 2011/2012 zeigt in der Spalte „Diff“ positive wie auch negative Werte. Theoretisch ist damit auch eine Differenz von 0 möglich; „Diff“ enthält daher Daten vom Typ Ganzzahlen. Die verbleibende Spalte „Pkt“ ist vom Typ her eine nonnegative Ganzzahl; es kann theoretisch Mannschaften geben, die eine Zeitlang nur verlieren und keine Punkte mitnehmen. An dieser Stelle klammern wir der Einfachheit halber Spezialregelungen aus, wie z.B. Punktabzüge. Unser Ziel ist das Erklären der Grundlagen der deskriptiven Statistik (und weniger des professionellen Fußballs als Wissenschaft, vgl. z.B. Jütting, 2004). Je nach Umständen können Punktabzüge als drastische Sanktionsmaßnahme durchaus zu negativen Punkteständen führen.
Bruchzahl
Eine Bruchzahl ist eine Zahl, deren Quotient Q = p / q einen Rest ungleich 0 aufweist. Ein Bruch ist genau dann gleich Null, wenn p = 0 und q ≠ 0. Solange die Länge der Nachkommastellen nicht unendlich oder nichtperiodisch ist, werden diese Bruchzahlen zu den rationalen Zahlen gezählt. Besitzt der Quotient Q = p / q einen Rest mit unendlichen (z.B. bei der Eulerschen Zahl, e oder Pi, µ) oder periodischen (z.B. 2/3 = 0,67) Nachkommastellen, so wird diese Bruchzahl zu den sog. irrationalen Zahlen gezählt. Ein Bruch wird in der sog. Inline-Schreibweise z.B. als Q = p / q, klassisch dagegen als
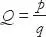 geschrieben. p ist dabei der Zähler, q der Nenner.
geschrieben. p ist dabei der Zähler, q der Nenner.
Die Tabelle zur Bundesligasaison 2011/2012 enthält ausschließlich Ganzzahlen. Bruchzahlen im Zusammenhang mit Bundesligaspielen findet man häufig im Zusammenhang mit Performanzstatistiken, z.B. zur Torgefährlichkeit, Passgenauigkeit, Zweikampfstärke usw. Aus der Bundesligatabelle lassen sich allerdings unkompliziert beispielhafte Bruchzahlen herleiten. Werden z.B. für Borussia Dortmund die durchschnittliche Anzahl der geschossenen Tore pro Spiel ermittelt, so ergibt sich über
■ Q = 80 / 34 als Bruchzahl
■ der Wert 2,353 (gekürzt),
■ 2,35294117647059 (weniger gekürzt) bzw.
■ 2,352941176470588235294117647059 (noch weniger gekürzt).
Solche scheinbaren „Präzisions exzesse“ können im Analysealltag durchaus ein Thema sein. Daher gleich ein paar Hinweise dazu:
Bei Brüchen werden die Konzepte von Genauigkeit und Präzision relevant. Die Genauigkeit(accuracy) einer Zahl ist durch die Anzahl von signifikanten Ziffern rechts von der Dezimalinterpunktion definiert. Die Präzision(precision) einer Zahl ist durch die Anzahl von signifikanten Ziffern insgesamt definiert. Bei der Addition bzw. Subtraktion wird die Anzahl der signifikanten Ziffern im Ergebnis durch den Wert mit der kleinsten Anzahl an signifikanten Ziffern bestimmt.
 Beispiele
Beispiele
Die Summe aus 1,2 + 1,24 + 1,248 ergibt theoretisch im Ergebnis den Wert 3,688. Dieser Wert ist jedoch scheinbar auf vier Stellen genau. Aufgrund der kleinsten Anzahl an signifikanten Ziffern beschränkt der Wert 1,2 die Anzahl von signifikanten Ziffern im Ergebnis auf eine Stelle nach dem Komma. Die Summe 1,2 + 1,24 + 1,248 sollte daher nur auf eine Stelle nach dem Komma gerundet als 3,7 ausgedrückt werden. Bei der Multiplikation und Division gilt Ähnliches. Die Genauigkeit des Produkts aus zwei oder mehr Zahlen hängt von der Anzahl signifikanter Ziffern rechts von der Dezimalinterpunktion im kleinsten Wert ab. Das Produkt aus 1,2 x 1,24 sollte daher auf eine Stelle nach dem Komma gerundet als 1,5 und nicht als 1, 488 angegeben werden.
Zu den Ziffern nach dem Interpunktionszeichen bei numerischen Werten sollte vielleicht noch ergänzend gesagt werden, dass mittels sog. Formate eingestellt werden kann, mit wie vielen Nachkommastellen die Zahlen angezeigt werden sollen. Standardmäßig werden Zahlen von -9999,99 bis 99999,99 dargestellt. Die Einstellung der Anzahl von Dezimalzellen bezieht sich dabei nur auf die Anzeige. Numerische Werte werden von der Software so präzise wie möglich, mit derzeit bis zu 32 Nachkommastellen, gespeichert.
Ziffern
Im letzten Abschnitt zu Bruchzahlen war von Ziffern die Rede. Was sind Ziffern? Ziffern stellen Zahlen dar. Die Dezimalziffern 1, 4 und 8 stellen z.B. zusammen die Zahl 1,488 aus dem vorangehenden Abschnitt dar. Die Ziffern 1, 4 und 8 wurden deshalb präzisierend als Dezimalziffern bezeichnet, weil sie und die im Beispiel beschriebene Zahl aus dem Dezimalsystem (Zehnersystem) stammen. Dieses Zahlensystem heißt Dezimalsystem, weil es zehn Ziffern (0 bis 9) umfasst bzw. die Zahl 10 zur Basis hat. Dieselbe Zahl kann, weil es neben dem Dezimalsystem weitere Zahlensysteme gibt, durchaus durch verschiedene Ziffern dargestellt werden. Die Bundesligatabelle ist, mit Ausnahme des Alphabets (für die Vereinsnamen), ausschließlich im Dezimalsystem. Wir werden daher auf andere Beispiele ausweichen müssen. Die folgende Tabelle stellt bspw. die Ziffernfolgen „1000“ und „10“ in ausgewählten Zahlensystemen dar (Dezimal, Hexadezimal, Dual-Binär, Wissenschaftliche Notation, Römisch). Darüber hinaus gibt es diverse weitere Zahlensysteme, z.B. Oktal.
Читать дальше

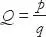 geschrieben. p ist dabei der Zähler, q der Nenner.
geschrieben. p ist dabei der Zähler, q der Nenner. Beispiele
Beispiele










