Christian FG Schendera - Deskriptive Statistik verstehen

■ Hemmungsloses Verallgemeinern(Merkmalsträger): Ein- und Ausschlusskriterien legen die Stichprobe, ggf. auch die Grundgesamtheit fest, auf die die deskriptive Statistik verallgemeinert werden kann. Mit dem „hemmungslosen Verallgemeinern“ ist ein Interpretieren über diese Grenzen hinaus gemeint. Häufige Verstöße sind z.B. (1) die deskriptive Statistik einer Stichprobe als die einer Grundgesamtheit zu überinterpretieren. Die deskriptive Statistik einer Stichprobe kann nicht auf eine Grundgesamtheit verallgemeinert werden. Aussagen über die Grundgesamtheit, allein auf der Grundlage von Stichproben daten, sind ohne Absicherung nicht zulässig. (2) Zu den Verstößen zählt auch, die deskriptive Statistik einer Teilmenge (z.B. alte Menschen) auch für andere Teilmengen (z.B. junge Menschen) zu verallgemeinern. (3) „Projektion“ ist z.B. die nicht seltene Praxis, z.B. bei der Korrelations- oder auch der Trendanalyse, die deskriptive Statistik über den Bereich der erhobenen Werte hinaus zu interpretieren.

■ jumping to conclusions(Extrapolieren und Schlussfolgerung innerhalb einer Erwartungshaltung, dem „frame“): Der Begriff „jumping to conclusions“ drückt, meine ich, schön aus, wie man bei der Interpretation der deskriptiven Statistik aus Begeisterung, und damit fehlender Zurückhaltung, leider vorschnellen Schlüssen über die darin wiedergegebenen Daten verfallen kann. Dieses „jumping to conclusions“ ist, meiner Erfahrung mit Statistik-Einsteigern nach, eine Erscheinungsform des gezielten Suchens von Zusammenhängen oder Unterschieden innerhalb eines Frames. Dieses Phänomen lässt sich wohl am besten als kognitiver Ersatz eines erwartungsgeleiteten Hypothesen tests umschreiben. Bei der Überinterpretation der deskriptiven Statistik (vor allem anhand von Stichproben) werden Unterschiede oder Zusammenhänge „gesehen“, die in Wirklichkeit in den beschriebenen Daten gar nicht vorkommen. Das „jumping to conclusions“ ist an sich gesehen nichts Schlechtes; allerdings sollte man diese „Schlussfolgerungen“ nicht als abgesichertes Ergebnis eines „Hypothesentests“ missverstehen, sondern als noch zu prüfende spekulative Annahme, die explizit einem echten Hypothesentest unterzogen werden sollte.

■ Der blinde Fleck(Schlussfolgerung außerhalb eines Frames): Während ein erwartungsgeleiteter „Hypothesentest“ dazu führt, dass „große“ Unterschiede (die gar nicht so groß sind) zwischen deskriptiven Parametern oft überschätzt werden, bezieht sich der „blinde Fleck“ auf Phänomene, die außerhalb der eigenen Erwartungshaltung (frame) liegen (Schendera, 2007, 165–169). Hier tritt der gegenteilige Effekt auf: Erwartungswidrige Effekte werden oft erst gar nicht wahrgenommen, geringe Unterschiede dagegen oft leider unterschätzt. Erfahrungsgemäß werden bei der Interpretation oft andere relevante Aspekte übersehen, z.B. die unterschiedliche Größe der miteinander verglichenen Gruppen (vgl. dazu auch die Stichworte Designstruktur, Auswahlwahrscheinlichkeit und Gewichtung).

Die deskriptive Statistik hat ihre Grenze eindeutig dann erreicht, sobald es nicht mehr um das Beschreiben einer Stichprobe, sondern um das Ziehen von Schlüssen über eine Grundgesamtheit geht, z.B. in Gestalt von Hypothesentests, Punkt- oder Intervallschätzungen. Ausgehend von Stichproben erlaubt die deskriptive Statistik keine Aussagen zur Grundgesamtheit. Die Inferenzstatistik wird in diesem Buch nicht behandelt; ich erlaube mir für ausgewählte Verfahren z.B. auf Schendera (2014 2, 2010) zu verweisen.

Diese Einführung in Sinn und Grenzen der deskriptiven Statistik fokussiert grundlegende Konzepte. Abgeschlossen werden soll mit einem Hinweis darauf, dass manche der erwähnten Begriffe, wie z.B. „Grundgesamtheit“, „Zufallsstichprobe“ und m.E. vor allem „Repräsentativität“ deutlich komplexer sind, als sie in dieser notwendigerweise vereinfachenden Darstellung womöglich anmuten (vgl. Prein et al., 1994). Allerdings beziehen sich Diskussion und Konzepte auf die Gültigkeit des Schlusses von einer „repräsentativen“ Zufallsstichprobe auf eine unbekannte Grundgesamtheit, was nicht Aufgabe der deskriptiven Statistik und damit auch nicht Gegenstand dieser Einführung ist.

2 Ein Heimspiel: Grundlagen der deskriptiven Statistik

„Fußball ist einfach, deshalb ist es ja so kompliziert.“

Berti Vogts

„Der Fußball ist einer der am weitesten verbreiteten religiösen Aberglauben unserer Zeit. Er ist heute das wirkliche Opium des Volkes.“

Umberto Eco

„The best thing about being a statistician is that you get to play in everyone else’s backyard.“

John Tukey, Bell Labs, Princeton University

Mit einem Heimspiel ist gemeint: Man spielt mit dem eigenen Team im eigenen Stadion vor eigenem Publikum. Man kennt sich bestens aus. Die Grundlagen der deskriptiven Statistik sind bekannt, man ist bestens vorbereitet. Heimspiel bedeutet also auch: Durch eine gute Vorbereitung hat man es selbst in der Hand, auch ein anspruchsvolles Auswärtsspiel in die Kontrollierbarkeit und Niveau eines Heimspiels zu wandeln.

Der Fokus von Kapitel 2 beschränkt sich daher auf Informationen in einer Datentabelle. Informationen, die man nicht notwendigerweise durch das Analysieren einer Datentabelle erfährt, also den Kontext von Daten, beschreibt dagegen Kapitel 3. Abschnitt 2.1beginnt daher mit einer der an Wochenenden wohl am häufigsten gesehenen Tabellen im deutschen Fernsehen, nämlich einer Bundesligatabelle. Das Ziel ist, anhand dieser Tabelle die wichtigsten Grundbegriffe der deskriptiven Statistik zu erläutern. Fußball erklärt also die deskriptive Statistik. Abschnitt 2.2beginnt mit dem Erläutern des Inhalts von Datentabellen und erläutert Begriffe wie z.B. Zahlen, Ziffern und Werte an Beispielen aus dem Fußball. Anschließend geht Abschnitt 2.3mit der Frage: „Was hat Messen mit meinen Daten zu tun?“ auf das sog. Messniveau einer Variablen ein. Anhand der Bundesligatabelle werden Messniveaus und ihre grundlegende Bedeutung für jede (nicht nur deskriptive) Statistik erläutert. Abschnitt 2.4hebt die Konsequenzen des Messniveaus für die praktische Arbeit mit Daten hervor. Begriffe wie z.B. Genauigkeit, Reliabilität und Validität sowie Objektivität werden z.B. mittels Torjägern veranschaulicht.

2.1 Fußball erklärt die deskriptive Statistik. Oder umgekehrt …?

„Fussball ist ding, dang, dong. Es gibt nicht nur ding.“

Giovanni Trappatoni

Man darf wahrscheinlich mit einiger Berechtigung annehmen, dass Fußball, zumindest jedes Wochenende, deutlich beliebter als Mathematik und Statistik sein könnte. Was liegt da näher, als die Faszination am Fußball auch ein wenig auf die deskriptive Statistik scheinen zu lassen? Im Folgenden wird die Abschlusstabelle der Bundesligasaison 2011/2012 wiedergegeben. Die Tabelle enthält die Spalten „Platz“, „Verein“, „Spiele“, „S“, „U“, und „N“ (jeweils für Sieg, Unentschieden oder Niederlage), „Tore“ sowie „Diff“ und „Pkt“.

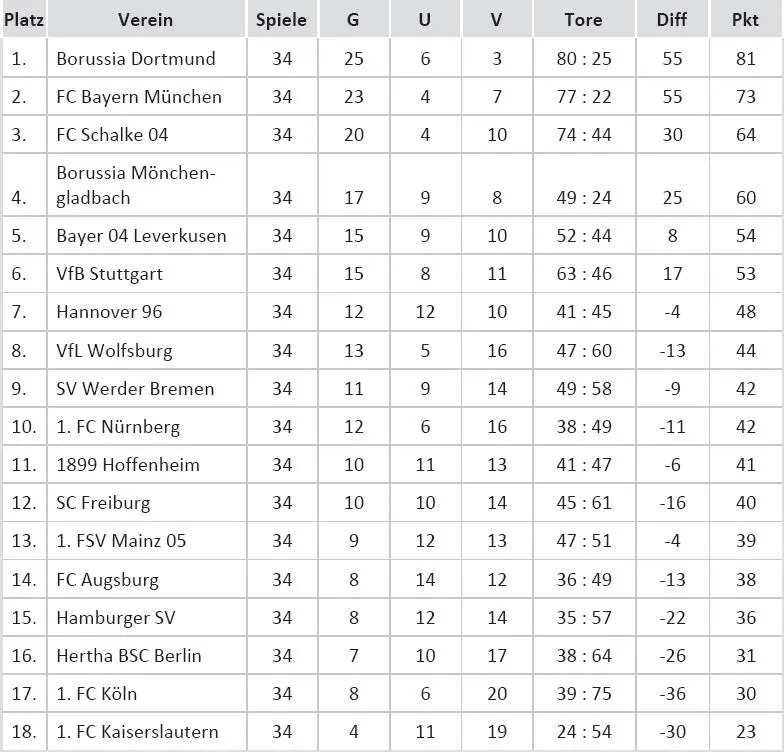
Abb. 2: Abschlusstabelle der Bundesligasaison 2011/2012

Das Ziel ist, anhand dieser Tabelle die wichtigsten Grundbegriffe der deskriptiven Statistik zu erläutern. Mit bestimmten Rängen gehen besondere Regelungen für sportliche Erfolge bzw. Misserfolge ein: Die ersten drei Mannschaften qualifizieren sich direkt für die Champions League. Die Mannschaft auf Platz 4 nimmt an der Champions-League-Qualifikation teil. Die Mannschaften auf Platz 5 bis 7 qualifizieren sich für die Europa League. Die Mannschaft auf Platz 16 kommt in die Relegation zur 2. Liga. Die beiden letzten Mannschaften steigen in die 2. Liga ab.