Christian FG Schendera - Deskriptive Statistik verstehen

■ welches inferenzstatistische Verfahren für meine gewählte Hypothese zulässig ist.

Nochmals: Das Messniveau ist wichtig! Wozu?

Kenne ich das Messniveau der auszuwertenden Daten , weiß ich, mit welchen passenden Maßen und Verfahren ich sie auswerten kann. Kenne ich das zugrunde liegende Messniveau der Maße und Verfahren, weiß ich, welche Daten ich damit auswerten kann. Die Kenntnis des Messniveaus ist wichtig für die Passung zwischen Daten und Maß bzw. Verfahren.

Für eine souveräne deskriptive Statistik schadet es also ganz und gar nicht, wenn das Messniveau der Daten selbst und die Grundlagen des Messens (zumindest in Grundzügen) bekannt sind. Was nun „Messen“ ist, versucht die Messtheorie als eine Art „Brücke“ zwischen der „wirklichen“ Welt und der Welt der „Zahlen“ zu definieren.

■ Messen ist demnach das Zuweisen von Zahlen zu Gegenständen, die eine bestimmte, empirisch beobachtbare Eigenschaft aufweisen. Eine gemessene Temperatur erhält z.B. eine bestimmte Gradzahl, eine bestimmte Laufstrecke erhält eine bestimmte Längenzahl.

■ Jedem Element aus dem empirischen Relativ wird dabei genau ein Element aus der Menge aller Zahlen ( numerisches Relativ ) zugeordnet. Die Laufstrecke A bekommt nur die Zahl A zugewiesen, aber nicht B oder C.

■ Zahlen (im sog. numerischen Relativ) müssen dabei dieselben Eigenschaften ausdrücken wie die beobachtbaren Gegenstände (im sog. empirischen Relativ). Wenn also die Laufstrecke A kleiner als Laufstrecke B ist, dann hat auch die zugewiesene Zahl für A kleiner als die für B zu sein.

Das Ziel ist, dass ein numerisches Relativ ein empirisches Relativ strukturgetreu abbildet . Sobald ein empirisches System auf ein numerisches System in der Weise eindeutig abgebildet wird, dass die empirischen Relationen innerhalb des empirischen Systems in den numerischen Relationen des numerischen Systems erhalten bleiben, liegt eine sog. Skala vor. Messen ist also die Bestimmung der Ausprägung einer Eigenschaft eines (Mess-)Objekts und die regelgeleitete Zuordnung von Zahlen zu Messobjekten . Liegt eine Skala vor, kann sie verschiedenen Messniveaus (Skalentypen) zugeordnet werden. Ein Messniveau kann anhand von Metadaten, Projektdokumentation oder, falls nicht vorhanden, anhand messtheoretischer Grundlagen mittels eines gesunden Menschenverstands in Erfahrung gebracht werden. Die Kenntnis der Skaleneigenschaften ist entscheidend. Jedes Skalenniveau macht erst bestimmte Maßzahlen, Grafiken oder auch statistische Verfahren sinnvoll. Auch Maße und Verfahren der deskriptiven Statistik setzen jeweils ein bestimmtes Messniveau voraus.

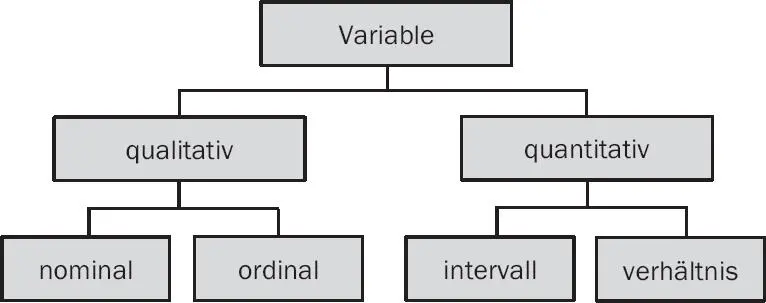
Abb. 3: Eine Systematisierung von Skalen- bzw. Messniveaus

In der Abbildung steigt das Skalenniveau von links („nominal“) nach rechts („verhältnis“) an. „verhältnis“ ist darin das höchste Skalenniveau, „nominal“ das niedrigste Skalenniveau. Jedes höhere Skalenniveau enthält auch die Merkmale der jeweils niedrigeren Niveaus. Je höher also das Skalenniveau, umso mehr Information bzw. komplexere Aussagen lassen sich mit einem geeigneten Maß bzw. Verfahren (z.B. der deskriptiven Statistik) „herausholen“. Welche, werden die Abschnitte 2.3.1bis 2.3.6erläutern.

Risiken: Informationsverlust, Unsinn und Klassierungen

Bei der Passung der Skalenniveaus der Daten und der Maße bzw. Verfahren sind u.a. drei Risiken zu vermeiden: der Informationsverlust, der errechnete Unfug und versteckte Klassierungen.

■ Informationsverlust: Für „niedrige“ Skalen konzipierte Maße (z.B. Modus) oder Verfahren (z.B. Häufigkeitsanalyse) können zwar auch auf höher skalierte Daten (z.B. Intervallniveau) angewendet werden, eben weil diese auch die Eigenschaften der niedrigeren Variablenniveaus (z.B. Nominalniveau) mit enthalten. Man muss sich aber klar sein, dass dies mit einem Informationsverlust verbunden ist: Der Informationsverlust besteht darin, dass „niedrigere“ Maße oder Verfahren außer Häufigkeit und Modus keine Aussagen über (je nachdem) größer / kleiner, Differenzen oder auch Verhältnisse erlauben, obwohl dies mit den vorliegenden Daten (z.B. auf Intervallniveau) möglich wäre, jedenfalls mit Maßen und Verfahren ab dem Intervallniveau.

■ „Errechneter Unfug“: Umgekehrt darf ich z.B. aus Daten auf Nominalniveau keinen Mittelwert bilden, weil dazu u.a. mindestens das Intervallniveau erforderlich ist. Abschnitt 2.3.1wird anhand von Rückennummern veranschaulichen, warum das Berechnen eines Mittelwerts aus Trikotnummern zwar mathematisch möglich, aber konzeptionell sinnfrei ist.

■ Gemeinerweise können ausgerechnet in Intervalldaten klassierte Extremwerte enthalten sein, z.B. anstelle der Werte 95, 96, 97 und 98 einfach die Information „>94“. Hier sollten die Aufmerksamkeitsglocken Alarm schlagen: Diese Kategorisierung hebt die Gleichheit der Abstände auf; es handelt sich also nicht mehr um ein Intervall-, sondern um ein Ordinalniveau. Ist dieser Hinweis sogar noch als Text hinterlegt, handelt es sich womöglich sogar nur noch um ein Nominalniveau.

Liegt also eine Skala vor, kann sie verschiedenen Niveaus (Skalentypen) zugeordnet werden. Das Bestimmen des Typs einer Skala, und die Zuordnung der Art und Menge der zulässigen Transformationen wird als „Eindeutigkeitsproblem“ bezeichnet. Als die am wenigsten eindeutige Skala gilt die Nominalskala (nur die eindeutige Zuordnung von Zahlen bzw. Namen zu Entitäten ist zulässig). Weitere Skalen sind die Ordinalskala (zstzl. größer-kleiner-Relation), Intervallskala (zstzl. Äquidistanz der Ränge) und die Verhältnisskala (zstzl. mit Nullpunkt).

Es gibt prinzipiell unendlich viele zulässige Transformationen und daher Möglichkeiten, weitere Skalenniveaus zu definieren. Je spezieller die zulässigen Transformationen sind, desto kleiner ist die Klasse gleichwertiger Skalen und desto größer ist die Eindeutigkeit einer Skala. Man sollte das Skalenniveau der vorliegenden Daten rechtzeitig vor einer deskriptiven Statistik abklären. In dieser Einführung werden einzelne grundlegende Konzepte (z.B. Messung und Skalierung, vgl. z.B. Nachtigall & Wirtz, 2008; Velleman & Wilkinson, 1993; Gigerenzer, 1981; Orth, 1974) nur gestreift, daraus soll jedoch keinesfalls nicht der Schluss abgeleitet werden, dass diese weniger relevant seien.

2.3.1 Nominalskala

Die Nominalskala gilt als die am wenigsten eindeutige Skala. Ihr Vorteil ist jedoch: Alle Daten besitzen auf jeden Fall das Nominalniveau, seien sie auch vom Format String/Text, Datum/Uhrzeit, oder auch beliebige Zahlen.

■ Definition: Messungen auf einer Nominalskala liegen dann vor, wenn die Ausprägungen von Merkmalen (1) gleichwertig, (2) Unterschiede oder Gemeinsamkeiten in den Ausprägungen der Merkmale feststellbar sind und wenn sich diese Ausprägungen zugleich (3) nicht in eine natürliche Rangfolge bringen lassen. Ein Merkmal kann anhand des Urteils „gleich“ oder „ungleich“ diskreten, exklusiv-disjunkten Ausprägungen (syn.: Klassen, Kategorien) zugeteilt werden. Ein Wert kann in eine und nur in eine Kategorie fallen.

■ Mögliche Aussagen: Gleichheit / Verschiedenheit: Zwei (oder mehr) einzelne (oder auch Gruppen von) Merkmalsträger(n) haben entweder das gleiche oder ein verschiedenes Merkmal.