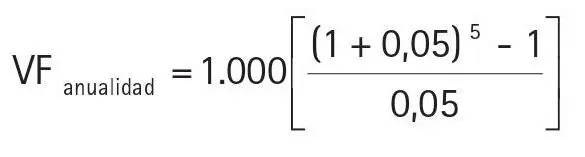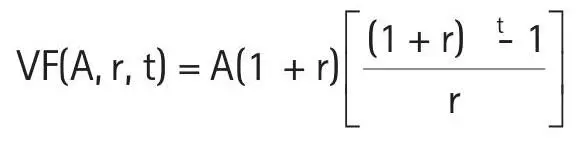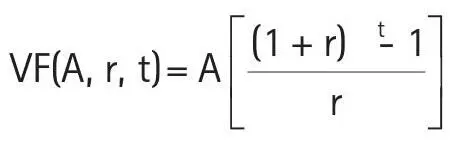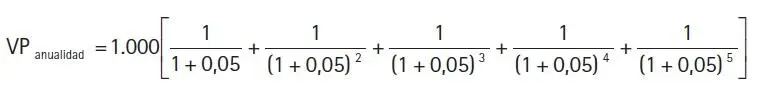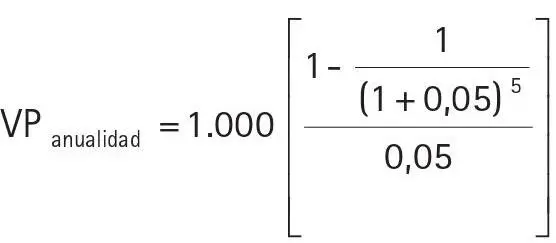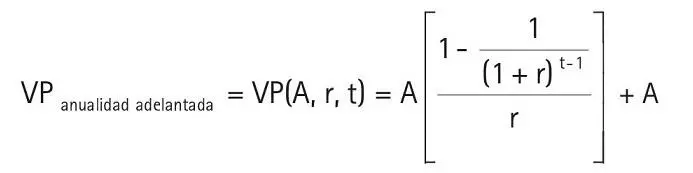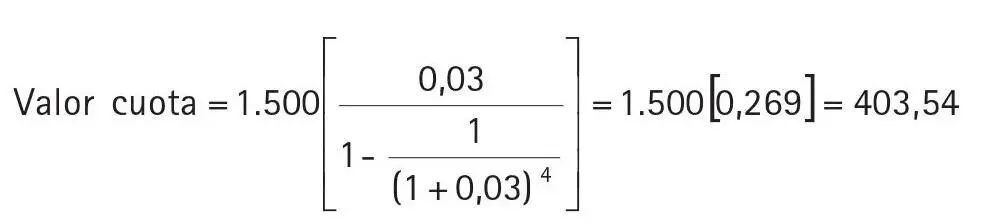El valor futuro de la anualidad será:
VFanualidad = 1.000(1+0,05)4 + 1.000(1+0,05)3 + 1.000(1+0,05)2 + 1.000(1+0,05) + 1.000
= 1.000[(1 + 0,05) 4+ (1 + 0,05)³ + (1 + 0,05)² + (1 + 0,05) + 1]
Expresión que se simplifica a:
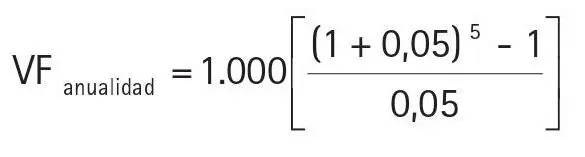
Generalizando, tendríamos la fórmula del valor futuro de una anualidad vencida:
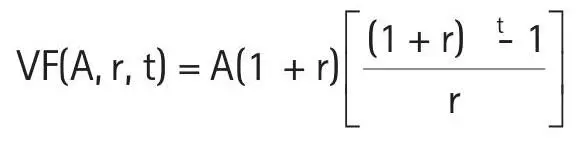
donde:
A: suma recibida al final de cada período (anualidad vencida)
r: tasa de interés por período
t: número de períodos
Si los flujos se recibieran al comienzo de cada año (gráfico 3.7) y no al final, cada uno de ellos generaría intereses por un año adicional y la fórmula del valor futuro cambiaría a la del:
Valor futuro de una anualidad adelantada:
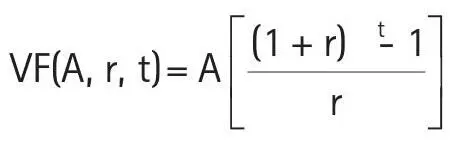
donde A representa la cantidad recibida o proporcionada al comienzo de cada período.
Gráfico 3.8 Flujo de una anualidad adelantada
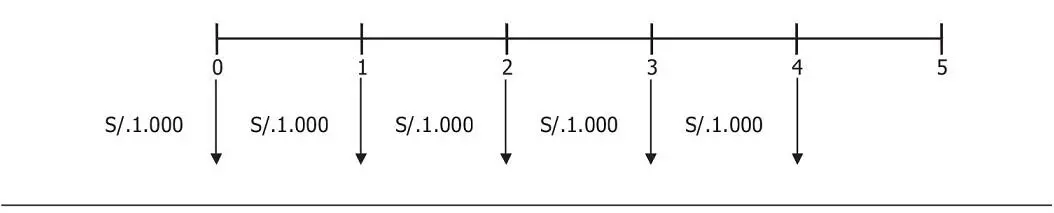
Fuente: elaboración propia.
Calcula el valor futuro al año 5 de dicho flujo.
3.1.2. Valor presente de una anualidad
El proceso es el inverso al seguido para el cálculo del valor futuro, como puede apreciarse en el gráfico 3.9 para anualidades vencidas.
Gráfico 3.9 Valor presente de una anualidad vencida
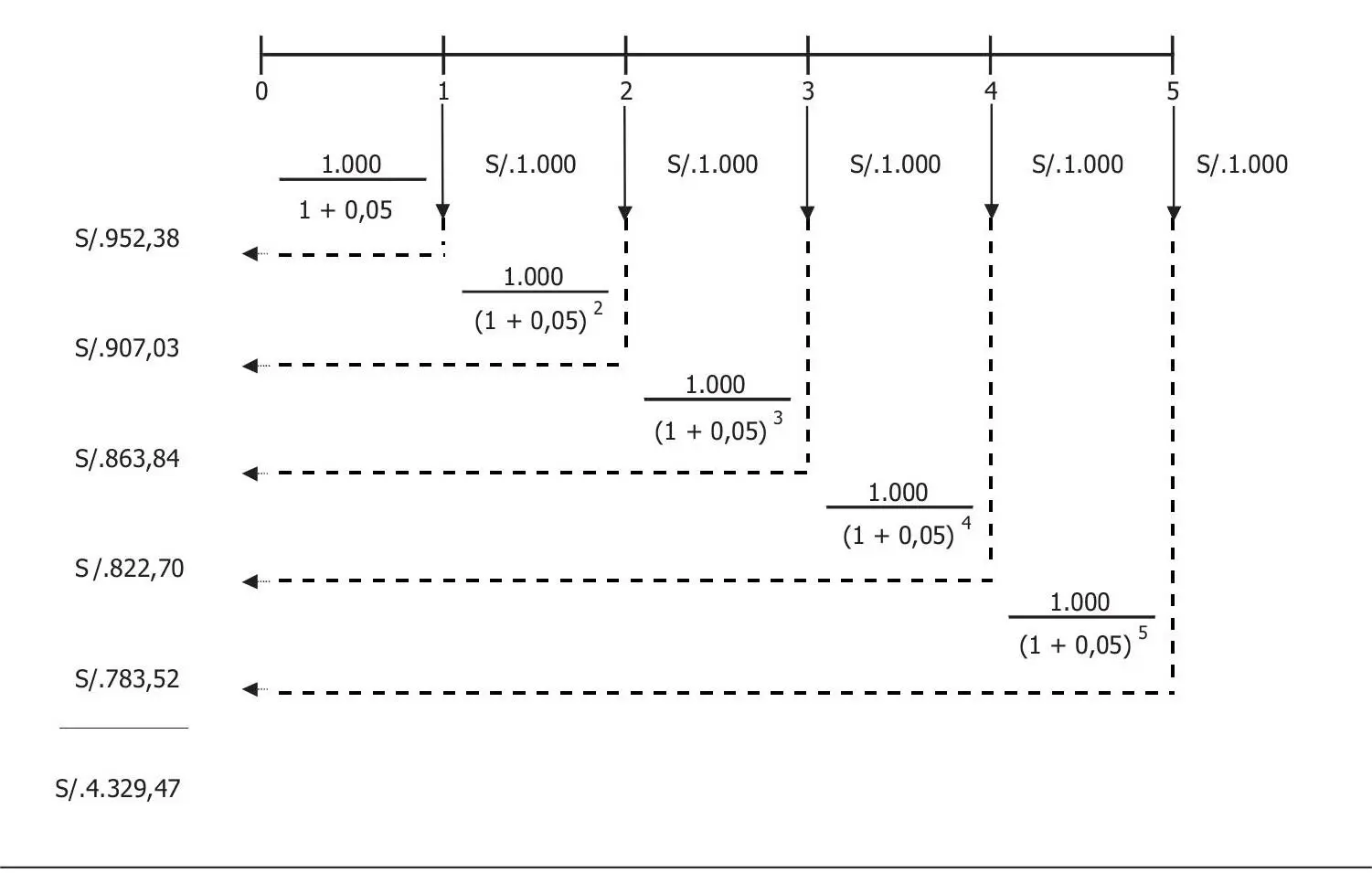
Fuente: elaboración propia.
El valor presente de la anualidad sería:
VP anualidad =
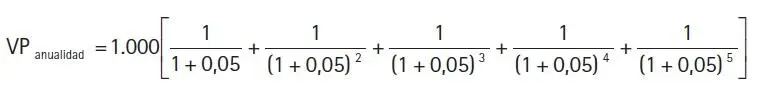
que se puede simplificar a:
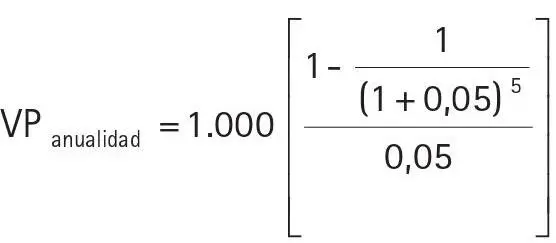
VPanualidad = 4.329,43
El valor presente de una anualidad vencida de S/.1.000 por período durante 5 años es de S/.4.329,47. Esta es la cantidad que tendría que depositar hoy en una cuenta que me pague el 5% y, así, poder retirar S/.1.000 al final de cada uno de los siguientes años y quedar con saldo cero en la cuenta.
En otras palabras, a una tasa de 5 , me es indiferente desembolsar S/.4.329,47 hoy o desembolsar S/.1.000 al final de cada año en los próximos 5 años. O, si yo fuera el que recibe el dinero, recibir S/.1.000 al final de cada uno de los siguientes 5 años es equivalente a recibir S/.4.329,47 hoy (valor presente del flujo del futuro).
Generalizando, el valor presente de una anualidad vencida es21:

A: suma anual recibida al final de cada período
r: tasa de interés por período
t: número de períodos
Si se tratara de una anualidad adelantada, el flujo sería como el que se muestra en el gráfico 3.10.
Gráfico 3.10 Valor presente de una anualidad adelantada
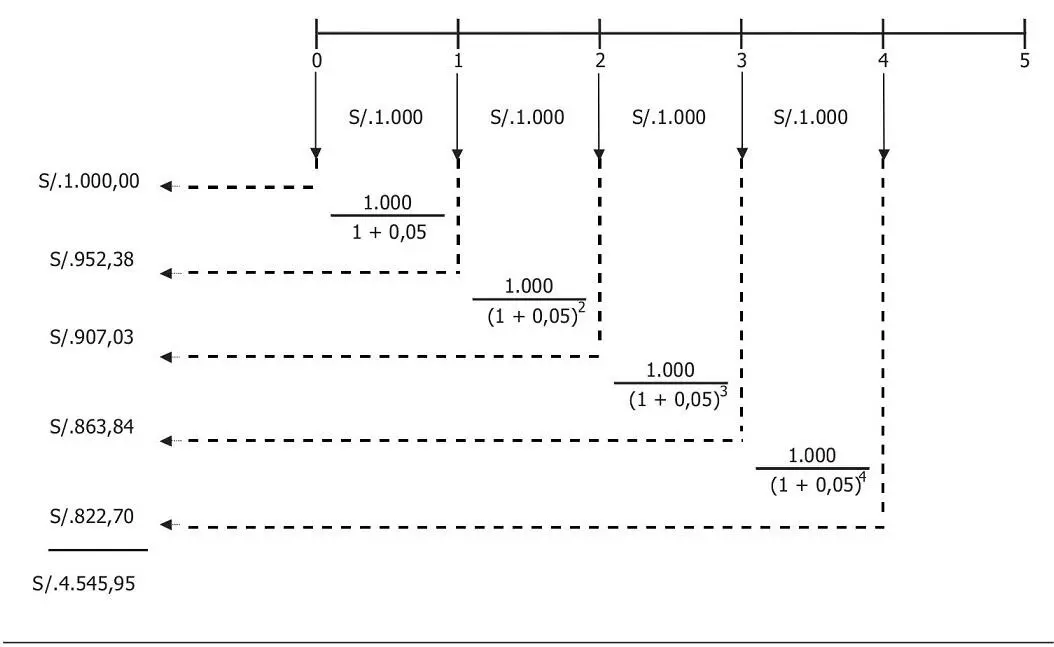
Fuente: elaboración propia.
El VP de una anualidad adelantada es mayor que el VP de la anualidad vencida, puesto que cada flujo se recibe un período antes.
La fórmula del valor presente de una anualidad adelantada es:
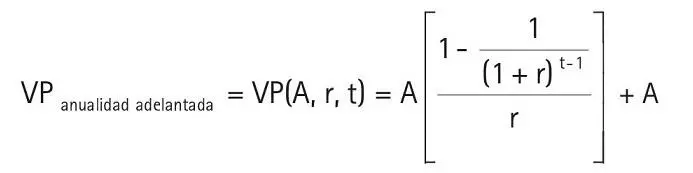
donde:
A: suma recibida o dada al comienzo de cada período
r: tasa de descuento por período
t: número de períodos
3.2. Anualidades, una aplicación: cronograma de pagos
¿Quién no ha tenido que comprar algo a plazos? Si tenemos el precio al contado, podemos calcular fácilmente el valor de cada cuota con la fórmula del valor presente de una anualidad si contamos con el número de cuotas y la tasa de interés. Despejando A de la fórmula del valor presente de una anualidad vencida, tenemos lo siguiente:
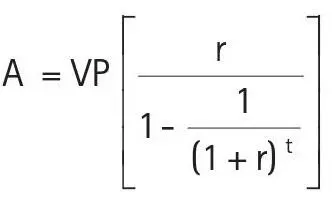
Si queremos comprar un televisor cuyo precio es de S/.1.500 y la tasa de interés es de 3% mensual, y deseamos pagarla en cuatro cuotas mensuales iguales, el valor de cada cuota se halla de la siguiente manera:
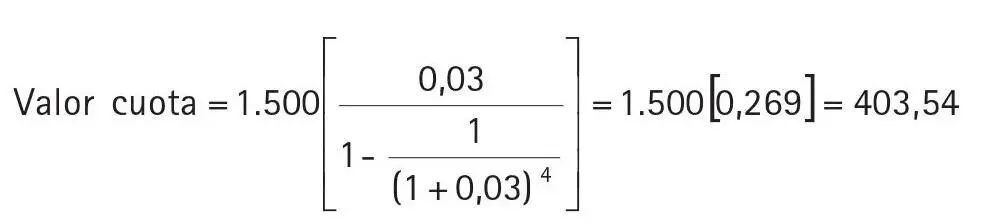
Cada cuota por pagar será de S/.403,54. Pero no sabemos (y muchas veces no nos interesa) qué parte de la cuota es el pago de intereses y qué parte es la amortización del préstamo.
Sin embargo, para una empresa es importante separarlos, pues los intereses son un gasto deducible para calcular las utilidades y los impuestos; y, por otro lado, necesita las amortizaciones para presentar adecuadamente el saldo de la deuda por pagar en el balance general. Para lograr esta separación, se elabora un cronograma de pagos.
Consideremos, por ejemplo, que la empresa La Agricultura Moderna S.A. desea comprar un tractor. Un proveedor norteamericano le ha ofrecido uno a un precio de US$1 millón al contado o pagar a crédito en 5 años, a una tasa estipulada del 12% que requiere pagos semestrales.
Como se requieren pagos cada 6 meses, estaríamos hablando de 10 cuotas o períodos en total. Como la tasa estipulada anual es 12% la tasa que se debe aplicar por semestre será de 12/2 = 6%22.
Cada cuota sería de:
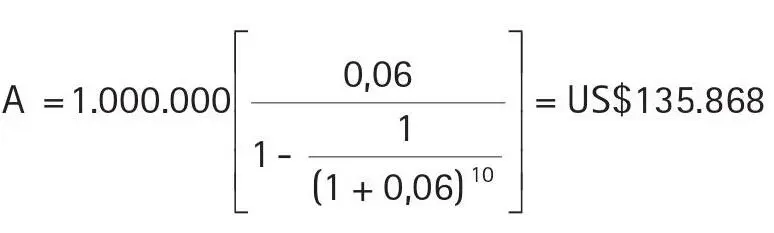
Con esta cuota, el precio y la tasa semestral, elaboramos el cronograma de pagos que se muestra en el cuadro 3.2. Observa que se han considerado anualidades vencidas.
Cuadro 3.2 Cronograma de pagos de cuotas iguales
| Período |
Saldo |
Cuota |
Interés |
Amortización |
Nuevo saldo |
| 1 |
1.000.000 |
135.868 |
60.000 |
75.868 |
924.132 |
| 2 |
924.132 |
135.868 |
55.448 |
80.420 |
843.712 |
| 3 |
843.712 |
135.868 |
50.623 |
85.245 |
758.467 |
| 4 |
758.467 |
135.868 |
45.508 |
90.360 |
668.107 |
| 5 |
668.107 |
135.868 |
40.086 |
95.782 |
572.325 |
| 6 |
572.325 |
135.868 |
34.340 |
101.528 |
470.797 |
| 7 |
470.797 |
135.868 |
28.248 |
107.620 |
363.176 |
| 8 |
363.176 |
135.868 |
21.791 |
114.077 |
249.099 |
| 9 |
249.099 |
135.868 |
14.946 |
120.922 |
128.177 |
| 10 |
128.177 |
135.868 |
7.691 |
128.177 |
0 |
Fuente: elaboración propia.
Читать дальше