Jesús Tong - Finanzas empresariales - la decisión de inversión

Sin embargo, en situaciones normales, en nuestro medio no es así, por lo que decimos que un sol ahora vale más que un sol recibido dentro de un año. Generalizando el concepto, el dinero recibido en diferentes años posee diferentes valores. Entonces, en una situación, sería errado considerar invertir S/.100 para recibir S/.40 en cada uno de los próximos 3 años y concluir que el beneficio neto sea igual a S/.20 (beneficio – costo = 120 – 100 = 20), ya que estaríamos sumando soles que se desembolsarían o recibirían en períodos de tiempo distintos y que, por lo tanto, tienen distinto valor. Habría que, antes de sumarlas, poner las cuatro cifras en un denominador común, es decir, un año común; por ejemplo, en soles del año 4 ó soles del año 0. Pero ¿cómo haríamos esto?

Empecemos por distinguir entre momento en el tiempo y período de tiempo:

Gráfico 3.1 Línea de tiempo

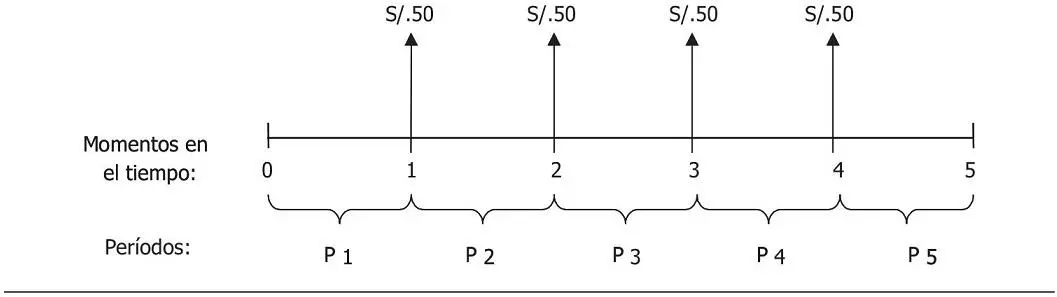
Fuente: elaboración propia.

En el gráfico 3.1, podemos observar los momentos (instantes) en el tiempo 0, 1, 2, 3, 4 y 5. El momento 0 se refiere al momento presente o actual. Nota que los períodos son lapsos de tiempo entre dos momentos. El período 1 (P 1) es el lapso de tiempo comprendido entre el momento 0 y el momento 1; el período 2 (P 2) es el lapso entre el momento 1 y el momento 2; y así sucesivamente.

Podemos observar que recibimos S/.50 al final de los períodos del 1 al 4. Notamos también que el final del período 1 (momento 1) es, a su vez, el comienzo del período 2. Si los S/.50 se recibieran no al final sino al comienzo de cada período, se tendría el flujo mostrado en el gráfico 3.2, que correspondería a un flujo de caja adelantado (el flujo del gráfico 3.1 es un flujo de caja vencido).

Gráfico 3.2 Flujo de caja adelantado

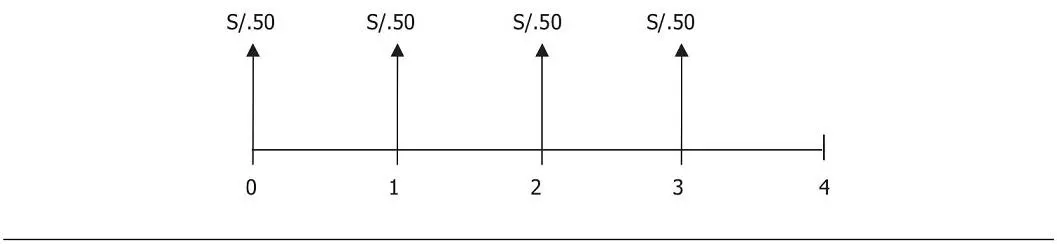
Fuente: elaboración propia.

A pesar de que en ambos casos se recibe la misma suma en cuatro momentos, el flujo de caja adelantado vale más, pues el dinero se recibe un año antes.

Hemos dicho que, para poder sumar los flujos recibidos en diferentes años, primero debemos convertirlos en flujos equivalentes en un momento común.

Si escogiéramos como momento común el día de hoy (el presente) y convirtiéramos cada flujo futuro en su equivalente de hoy, estaríamos realizando un proceso de descuento y cada flujo futuro traído a su valor de hoy sería el valor presente (VP).

Si, por el contrario, escogiéramos una fecha común futura y cada flujo lo convirtiéramos hacia (adelante) una fecha futura, estaríamos hablando de un proceso de composición cuyo resultado sería el valor futuro (VF).

Gráfico 3.3 Proceso de descuento

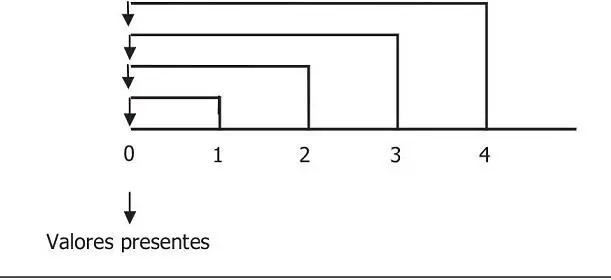
Fuente: elaboración propia.

Gráfico 3.4 Proceso de composición

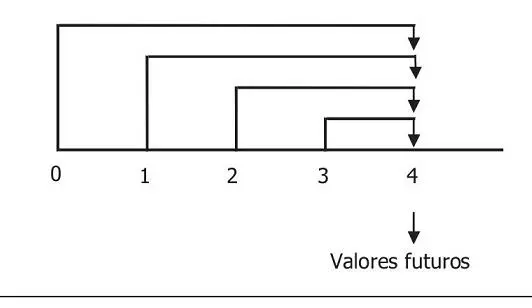
Fuente: elaboración propia.

Supongamos que Jorge tiene S/.500 hoy y que los deposita en el Banco Sudamericano que le paga 6% de interés anual y lo deja permanentemente. ¿Cuánto tendría en un año? ¿En dos, tres y cinco años? En un año, habría ganado el 6% de S/.500, es decir, S/.30,00 y tendría 500 + 30 = S/.530,00; es decir, 500(1 + 0,06) = S/.530. Al final del segundo año, ganaría intereses de S/.530 x 0,06 = S/.61,80 y tendría 500 + 61,80 = S/.561,80; o el valor futuro al final del segundo año sería:

500(1 + 0,06)(1 + 0,06) = 500(1,06)2 = 561,8

Podemos hacer el mismo ejercicio para tres, diez y «t» años. Obtendríamos los resultados mostrados en el gráfico 3.5.

Gráfico 3.5 Cálculo del valor futuro de una inversión a distintos períodos

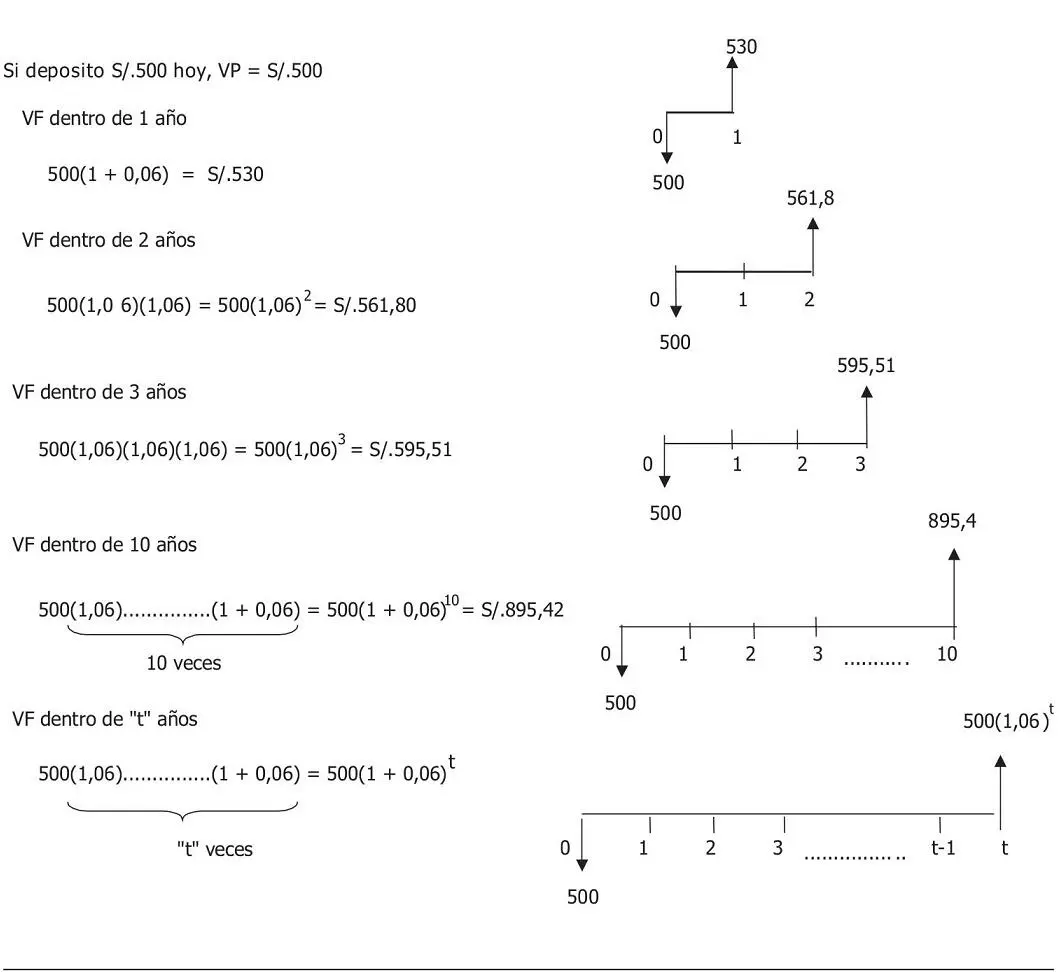
Fuente: elaboración propia.

Generalizando, si llamamos VP al valor presente (hoy), VF al valor futuro después de «t» períodos y «r» a la tasa de interés, tendríamos la siguiente relación:

VFt = VP(1 + r)t (3.1)

La expresión 3.1 es una fórmula con cuatro variables. Conociendo tres de ellas, podemos hallar la cuarta con facilidad.

El proceso de descuento es exactamente lo opuesto al proceso de composición. Al tener el flujo de efectivo que se recibirá al final del período «t», VFt, ¿cuál es el valor presente (VP) que equivaldría al flujo futuro mencionado si la tasa de interés vigente fuera «r»? Si despejamos el término VP en la expresión 3.1, obtendríamos la fórmula del valor presente:

Es decir, si recibiéramos S/.1.000, dentro de un año (t=1), con una tasa de descuento de 10%, su VP sería:

Si la suma se recibiera dentro de 5 años, entonces, VF 5= 1.000 y el VP sería:

Una forma de interpretar el valor presente es pensar en qué suma debo depositar hoy, a la tasa de interés vigente, para que al final del año «t» tenga la suma de flujo futuro. En nuestro ejemplo, tenemos que depositar S/.620,73 hoy para tener al final del quinto año, con una tasa de 10%, la cantidad de S/.1.000. En resumen, el valor presente de S/.1.000 recibidos al final del quinto año con una tasa de descuento de 10% es de S/.620,73. Es decir, S/.1.000 recibidos al final del año 5 son equivalentes a tener S/.620,73 hoy si la tasa de descuento es 10%.

Veamos el siguiente ejemplo. Un alumno desea seguir una maestría después de terminar su carrera dentro de tres años. Si su maestría le cuesta S/.70.000, monto que tendrá que desembolsar cuando empiece sus estudios (comienzo del cuarto año), ¿cuánto tendría que depositar en una cuenta que le paga 6% anual para contar exactamente con la suma necesitada al iniciar su maestría?

Se plantea como un problema de valor presente:

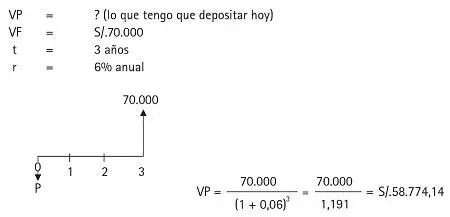
Necesitará depositar S/.58.774,14.

Para terminar este acápite, conviene recalcar dos hechos: primero, cuanto más alejada en el tiempo se encuentre una suma de dinero, menor será su valor presente; segundo, cuanto mayor sea la tasa de descuento19, menor será el valor presente. El gráfico 3.6 nos muestra el valor presente de US$1 para diferentes tasas y períodos.

Gráfico 3.6 Valor presente de US$1 para diferentes tasas y períodos

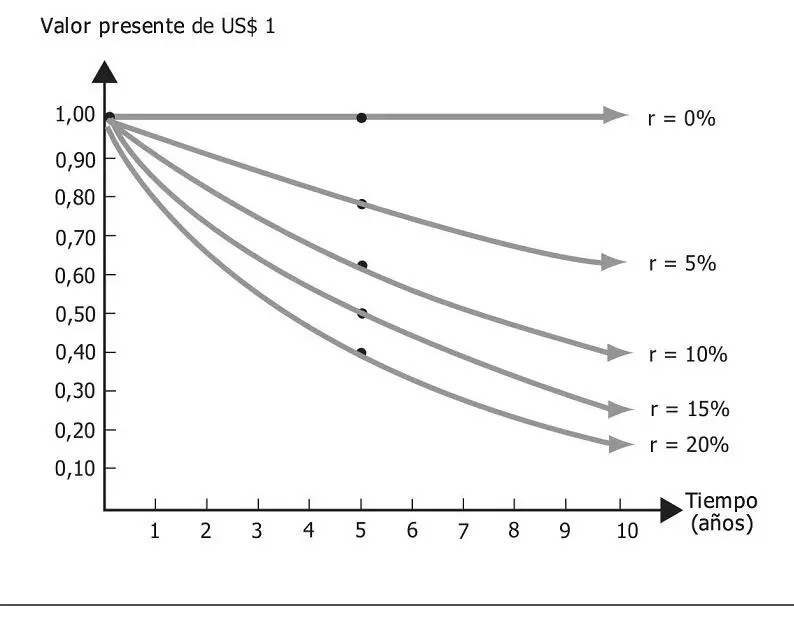
Fuente: Ross et al. 1997: 42.