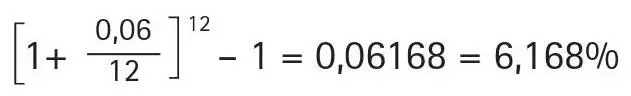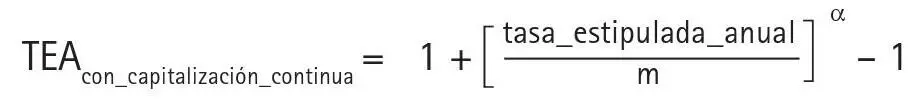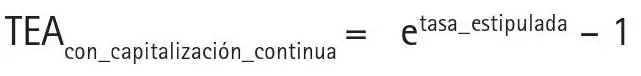Nota que el valor presente se mantiene en 1 cuando la tasa de interés es cero.
2.3. Interés simple o interés compuesto
Son dos formas de considerar el interés ganado. En el caso del interés simple, el interés se calcula siempre sobre el monto inicial depositado. Si deposito S/.1.000 al 10% durante tres años, cada año el interés ganado será de 0,1 x 1.000 = S/.100 y podré retirar S/.1.300 al cabo de los tres años.
En el caso del interés compuesto, el interés ganado en cada año se agrega al capital inicial para obtener el capital final sobre el que se aplicarán los intereses el próximo período en un proceso que se denomina «capitalización de los intereses». Los intereses se incorporan al capital para ganar más intereses el siguiente período. Es decir, se ganan intereses sobre intereses. El cuadro 3.1 muestra el proceso.
Cuadro 3.1 Proceso de capitalización de intereses
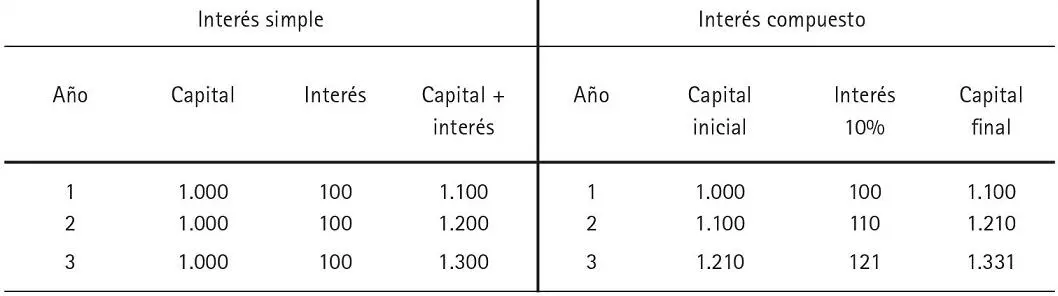
Fuente: elaboración propia.
Notamos que, en el caso del interés compuesto, el capital final de un período es el capital inicial del siguiente.
El hecho de utilizar interés compuesto me hubiera hecho ganar S/.31 más (331 – 300) por intereses.
Comúnmente, en nuestra vida diaria, utilizamos el interés compuesto, que es lo que consideraremos a lo largo del libro, a menos que indiquemos, específicamente, que se trata de interés simple.
2.4. Frecuencia de composición o descuento
En los ejemplos anteriores, los flujos de caja fueron compuestos o descontados anualmente.
¿Qué sucedería si la composición o el descuento fuera más frecuente, digamos cada seis meses o mensualmente?
En un caso anterior, vimos que, si depositamos S/.500 por un período de 10 años con una tasa de interés de 6% anual capitalizable (o compuesto) anualmente, el valor futuro sería:
VF10 = 500(1 + 0,06)10 = 895,42
Si se mantuviera la tasa estipulada de 6% anual, pero se capitalizaran los intereses cada seis meses (se calcularan los intereses cada seis meses y se agregaran al capital), tendríamos que cada semestre se ganaría 6/2 = 3% y tendríamos en total 20 semestres. El valor futuro se calcularía de la siguiente manera:
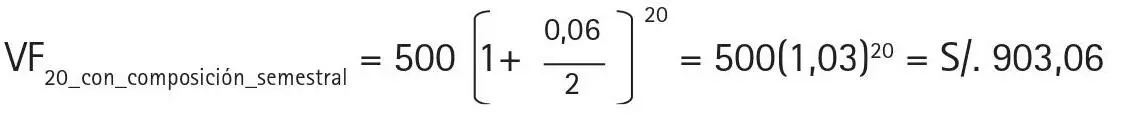
La diferencia de S/.7,64 (903,06 – 895,42) proviene de la composición más frecuente de los intereses. El interés ganado y, por lo tanto, la tasa ganada serán mayores cuanto más frecuente sea la capitalización de los intereses.
Si la composición fuera mensual, se tendría:

Si llamamos TES a la tasa estipulada anual20 (0,06 ó 6 ); «m», al número de composiciones por año; y «t», al número de años, tendríamos:
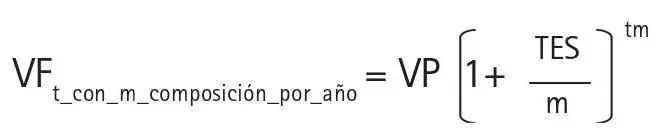
Para una tasa estipulada, la tasa ganada en realidad —llamada «tasa efectiva»— será mayor cuanto mayor sea el número de composiciones (capitalizaciones) por año. En términos de tasas, tendríamos la siguiente relación:
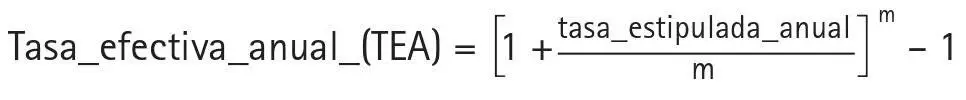
En el depósito de los S/.500, la tasa efectiva anual sería:
con composición semestral TEA = 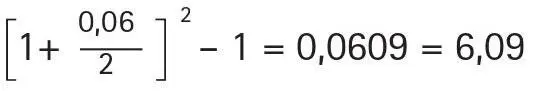 con composición mensual TEA =
con composición mensual TEA = 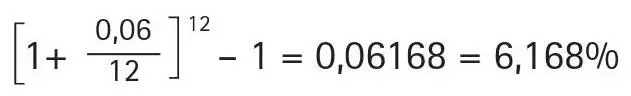
¿Qué pasa si elevamos el número de composiciones al límite, es decir, si componemos cada segundo? Si hacemos «m» infinito, tendríamos lo que se llama «composición o capitalización continua». La tasa efectiva para este caso será:
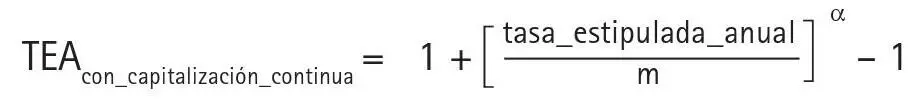
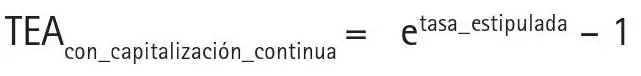
donde «e» es la base de los logaritmos neperianos.
En Estados Unidos, la tasa estipulada recibe el nombre de APR (annual percentage rate) y las empresas están obligadas a informarla a los clientes. Con ello, el costo verdadero (la tasa efectiva) queda indeterminado si no se precisa el período de composición. Si la tasa cobrada mensual es 1%, el APR será 1% x 12 = 12%.
En el Perú, la Superintendencia de Banca y Seguros (SBS) obliga a las instituciones financieras a publicar la tasa efectiva anual que aplican a sus clientes.
Para hallar la tasa que se debe cobrar por período de composición (semestral o mensual), habrá que utilizar:
Tasa_por_período = [1 + TEA] ^(1/m)
Así, si queremos cobrar una TEA de 6% anual:
Tasa efectiva semestral = T_Esemestral = [1 + 0,06]^1/2 = 0,02956 = 2,956%
Tasa efectiva mensual = T_Emensual = [1 + 0,06]^1/12 – 1 = 0,04868 = 0,4868%
3. Anualidades y perpetuidades
Con lo que hemos aprendido hasta ahora nos es posible hallar el valor presente (o el valor futuro a un momento determinado) de cualquier flujo o corriente de efectivo que tengamos en un período dado, digamos cinco o diez años. Basta con traer cada flujo futuro a su valor presente y sumarlos. Sin embargo, este sería un camino largo en el que tendríamos que repetir la operación de calcular el valor presente muchas veces (una por cada período).
Cuando se dan ciertas condiciones, que detallaremos a continuación, el proceso puede simplificarse a la aplicación de una fórmula una sola vez. Son los casos que veremos a continuación.
Se define como una anualidad a una corriente de flujos de efectivo que ocurre a intervalos regulares durante un período determinado de tiempo.
3.1.1. Valor futuro de una anualidad
Si nos comprometemos a depositar S/.1.000 al final de cada año durante los próximos 5 años en una cuenta, al 5% anual, ¿cuánto tendríamos al final del año 5?
Gráfico 3.7 Valor futuro de una anualidad
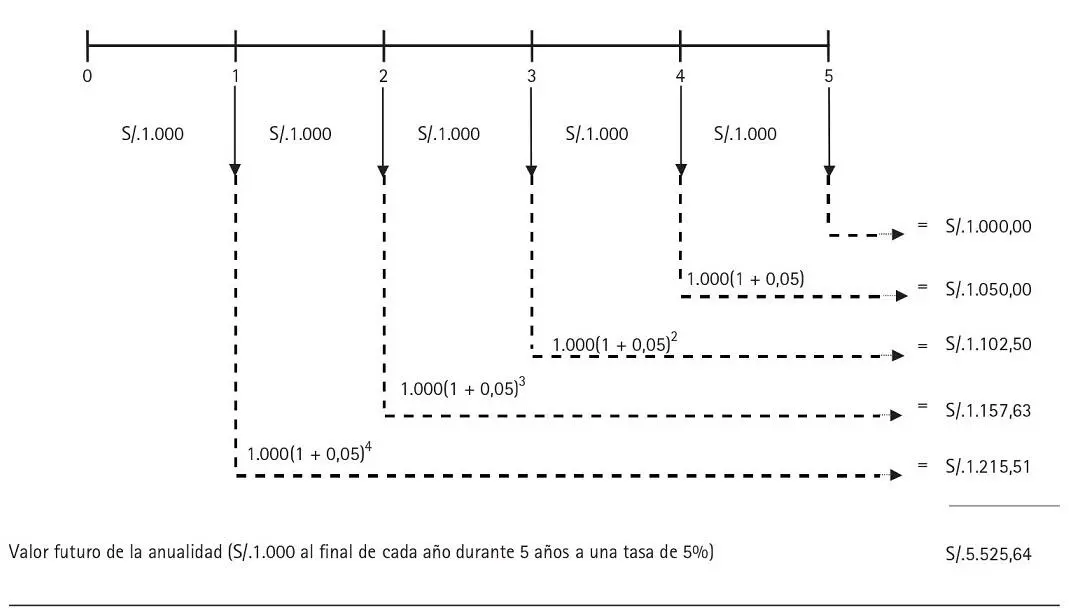
Fuente: elaboración propia.
El gráfico 3.7 muestra el flujo de caja y el cálculo del valor futuro al llevar las cinco anualidades al final del año 5.
Los S/.1.000 recibidos al final del período 1 generarán intereses por 4 años; los recibidos al final del año 2, por 3 años; los recibidos al final del año 3, por 2; los recibidos al final del año 4, por 1; y, finalmente, los recibidos al final del año 5 están ya en el período 5, por lo que no ganan intereses.
Читать дальше


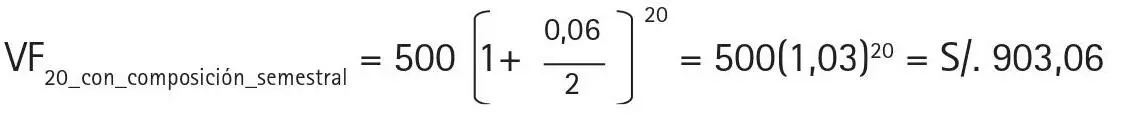

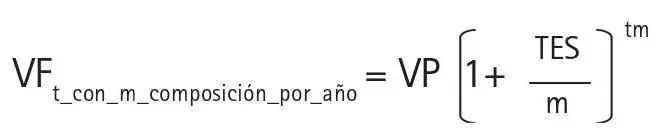
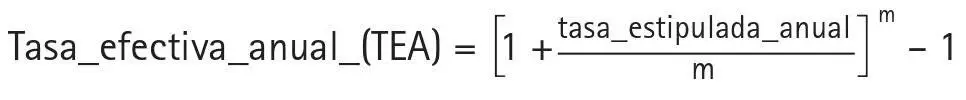
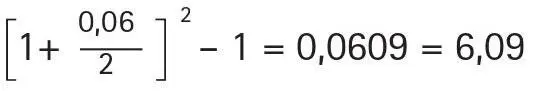 con composición mensual TEA =
con composición mensual TEA =