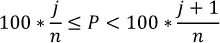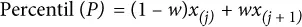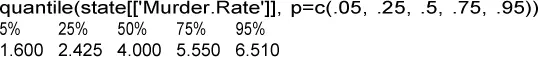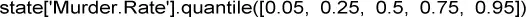Peter Bruce - Estadística práctica para ciencia de datos con R y Python

Una medida habitual de la variabilidad es la diferencia entre el percentil 25 y el percentil 75, al que se llama rango intercuartílico ( interquartile range ) (o IQR). Veamos un sencillo ejemplo: {3,1,5,3,6,7,2,9}. Los ordenamos para obtener {1,2,3,3,5,6,7,9}. El percentil 25 está en 2.5 y el percentil 75 está en 6.5, por lo que el rango intercuartílico es 6.5 – 2.5 = 4. El software puede tener enfoques ligeramente diferentes que producen diferentes respuestas (consultar el consejo que aparece más abajo). Normalmente, estas diferencias son mínimas.

Para conjuntos de datos muy grandes, calcular percentiles exactos puede ser muy costoso desde el punto de vista del cálculo, ya que requiere ordenar todos los valores de los datos. El aprendizaje automático y el software estadístico utilizan algoritmos especiales [Zhang-Wang, 2007] para obtener un percentil aproximado que se puede calcular con mucha rapidez y tiene garantizada una cierta precisión.

Si tenemos un número par de datos ( n es par), entonces el percentil es ambiguo según la definición anterior. De hecho, podríamos tomar cualquier valor entre los estadísticos de orden x (j)y x (j + 1), donde j satisface:

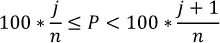
Formalmente, el percentil es el promedio ponderado:

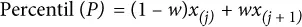
para alguna ponderación w entre 0 y 1. El software estadístico tiene enfoques ligeramente diferentes para elegir w . De hecho, la función quantile de R ofrece nueve alternativas diferentes para calcular el cuantil. A excepción de los conjuntos de datos pequeños, normalmente no es necesario preocuparse por la forma precisa en que se calcula el percentil. En el momento de escribir estas líneas, numpy.quantile de Python solo admite un enfoque: la interpolación lineal.

La tabla 1.3(repetición de la tabla 1.2para hacerlo más cómodo) muestra las primeras filas del conjunto de datos que contienen las tasas de población y de los homicidios para cada estado.

Tabla 1.3Algunas filas de data.frame de la situación de la población y la tasa de homicidios por estados

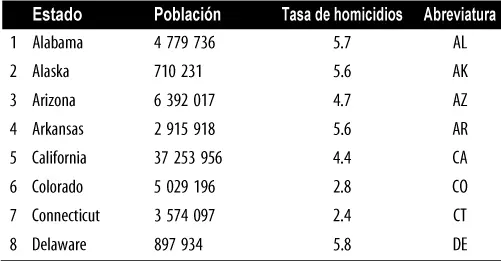
Utilizando las funciones integradas de R para la desviación estándar, el rango intercuartílico (IQR) y la desviación absoluta mediana de la mediana (MAD), podemos calcular las estimaciones de variabilidad para los datos de la población estatal:

El marco de datos de pandas proporciona métodos para calcular la desviación estándar y los cuantiles. Usando los cuantiles, podemos determinar fácilmente el IQR. Para la MAD robusta, usamos la función robust.scale.mad del paquete statsmodels:

La desviación estándar es casi dos veces mayor que la MAD (en R , por defecto, la escala de la MAD se ajusta para estar en la misma escala que la de la media). Este hecho no es sorprendente, ya que la desviación estándar es sensible a valores atípicos.

Ideas clave

• La varianza y la desviación estándar son los estadísticos de variabilidad más difundidos y de los que más se informa de manera rutinaria.

• Ambos son sensibles a los valores atípicos.

• Entre las métricas más robustas se encuentran la desviación absoluta media, la desviación absoluta mediana de la mediana y los percentiles (cuantiles).

• El recurso de estadísticos en línea de David Lane tiene una sección sobre percentiles

( https://onlinestatbook.com/2/introduction/percentiles.html ).

• Kevin Davenport tiene una publicación interesante en R -Bloggers ( https://www.rbloggers.com/2013/08/absolute-deviation-around-the-median/ ) sobre las desviaciones de la mediana y sus propiedades robustas.

Cada una de las estimaciones que tratamos aquí resume los datos en una sola cifra para describir la localización o la variabilidad de los datos. También es interesante explorar cómo se distribuyen los datos en general.

Términos clave de la exploración de la distribución

Diagrama de caja

Diagrama presentado por Tukey para visualizar de forma rápida la distribución de datos.

Sinónimo

diagrama de caja y bigotes

Tabla de frecuencias

Registro del recuento de valores de datos numéricos que caen en un conjunto de intervalos (contenedores).

Histograma

Diagrama de la tabla de frecuencias con los contenedores o intervalos en el eje x y el recuento (o proporción) en el eje y. Aunque los gráficos de barras son visualmente similares, no deben confundirse con los histogramas. Consultar “Exploración de datos binarios y categóricos” en la página 27para obtener más información sobre las diferencias entre ambas presentaciones.

Diagrama de densidad

Versión suavizada del histograma, a menudo basada en una estimación de la densidad del núcleo ( kernel density estimate ).

En "Estimación basada en percentiles" en la página 16, exploramos cómo se pueden utilizar los percentiles para medir la dispersión de los datos. Los percentiles también son útiles para extraer un resumen de toda la distribución. Es habitual informar los cuartiles (percentiles 25, 50 y 75) y los deciles (percentiles 10, 20,…, 90). Los percentiles son especialmente indicados para extraer el resumen de las colas ( tails ) (partes de los extremos del rango) de la distribución. La cultura popular ha acuñado el término de los uno por ciento ( one-percenters ) para referirse a las personas con una riqueza superior al percentil 99.

La tabla 1.4muestra algunos percentiles de la tasa de homicidios por estados. En R , esta información la facilita la función quantile:

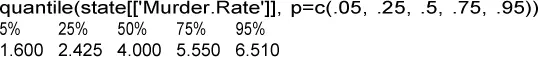
En Python la proporciona el método quantile del marco de datos de pandas:

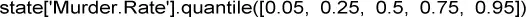
Tabla 1.4Percentiles de tasa de homicidios por estados