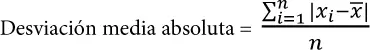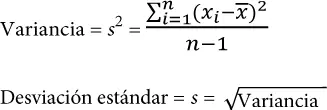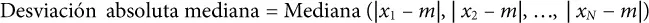Peter Bruce - Estadística práctica para ciencia de datos con R y Python

La diferencia entre el mayor y el menor valor de un conjunto de datos.

Estadísticos ordinales

Métricas basadas en los valores de datos ordenados de menor a mayor.

Sinónimo

rangos

Percentil

Valor tal que el P por ciento de los valores toma este valor o un valor inferior y para (100 – P) el porcentaje toma este valor o un valor superior.

Sinónimo

cuantil

Rango intercuartil

Diferencia entre el percentil 75 y el percentil 25.

Sinónimo

IQR

Así como existen diferentes formas de medir la localización (media, mediana, etc.), también existen diferentes formas de medir la variabilidad.

Las estimaciones de la variación más utilizadas se basan en las diferencias o desviaciones ( deviations ) entre la estimación de la localización y los datos observados. Para un conjunto de datos {1, 4, 4}, la media es 3 y la mediana es 4. Las desviaciones de la media son las diferencias: 1 - 3 = –2, 4 - 3 = 1, 4 - 3 = 1. Estas desviaciones nos dicen lo dispersos están los datos en torno al valor central.

Una forma de medir la variabilidad es estimar un valor típico para estas desviaciones. El promedio de las desviaciones en sí no nos diría mucho: las desviaciones negativas compensan las positivas. De hecho, la suma de las desviaciones de la media es precisamente cero. En cambio, un enfoque sencillo consiste en extraer el promedio de los valores absolutos de las desviaciones de la media. En el ejemplo anterior, el valor absoluto de las desviaciones es {2 1 1} y su promedio es (2 + 1 + 1) / 3 = 1.33. A esta medida se conoce como desviación media absoluta ( mean absolute deviation ) y se calcula con la fórmula:

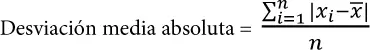
donde x es la media muestral.

Las estimaciones de variabilidad más conocidas son la varianza ( variance ) y la desviación estándar ( standard deviation ), que se calculan a partir del cuadrado de las desviaciones. La varianza es un promedio del cuadrado de las desviaciones y la desviación estándar es la raíz cuadrada de la varianza:

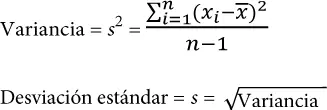
La desviación estándar es mucho más fácil de interpretar que la varianza, ya que está en la misma escala que los datos originales. Aun así, con su fórmula más complicada y menos intuitiva, podría parecer peculiar que en estadística se prefiera la desviación estándar a la desviación media absoluta. Debe su supremacía a la teoría estadística, ya que trabajar matemáticamente con valores al cuadrado es mucho más conveniente que con valores absolutos, especialmente en el caso de modelos estadísticos.

Grados de libertad, y ¿ n o n – 1?

En los libros de estadística, siempre se discute por qué tenemos n – 1 en el denominador en la fórmula de la varianza, en lugar de n, lo que conduce al concepto de grados de libertad ( degrees of freedom ). Esta distinción no es importante ya que n es generalmente lo suficientemente grande como para que no haya mucha diferencia si dividimos entre n o n – 1. Pero en caso de que sea de interés, lo explicamos a continuación. Se fundamenta en la premisa de que deseamos hacer estimaciones sobre una población, basándonos en una muestra.

Si usamos el denominador intuitivo de n en la fórmula de la varianza, subestimaremos el valor real de la varianza y la desviación estándar en la población. Esto se conoce como estimación sesgada ( biased ). Sin embargo, si dividimos por n – 1 en lugar de n , la varianza se convierte en una estimación no sesgada ( unbiased ).

Explicar completamente por qué el uso de n conduce a una estimación sesgada implica la noción de grados de libertad, que tiene en cuenta el número de restricciones al calcular una estimación. En este caso, hay n – 1 grados de libertad, ya que hay una restricción: la desviación estándar depende del cálculo de la media muestral. Para la mayoría de los problemas, los científicos de datos no necesitan preocuparse por los grados de libertad.

La varianza, la desviación estándar y la desviación absoluta mediana son robustas a valores atípicos y extremos (consultar "Estimación de medianas robustas" en la página 10, donde se desarrolla un debate sobre estimaciones robustas para la localización). La varianza y la desviación estándar son especialmente sensibles a los valores atípicos, ya que se basan en las desviaciones al cuadrado.

Una estimación robusta de la variabilidad es la desviación absoluta mediana de la mediana ( median absolute deviation from the median ) o MAD:

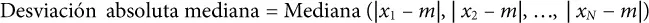
donde m es la mediana. Al igual que la mediana, la MAD no se ve influenciada por valores extremos. También es posible calcular la desviación estándar truncada análoga a la media truncada (consultar "Media" en la página 9).

La varianza, la desviación estándar, la desviación media absoluta y la desviación absoluta mediana no son estimaciones equivalentes, incluso en el caso de que los datos provengan de una distribución normal. De hecho, la desviación estándar es siempre mayor que la desviación absoluta media, que a su vez es mayor que la desviación absoluta mediana. A veces, la desviación absoluta mediana se multiplica por un factor de escala constante para adaptarla a la misma escala que la desviación estándar en el caso de una distribución normal. El factor que se utiliza normalmente de 1.4826 significa que el 50% de la distribución normal cae dentro del rango ± MAD.

Un enfoque diferente para estimar la dispersión se centra en observar la distribución de los datos ordenados. Los estadísticos que tienen como base los datos ordenados (clasificados) se denominan estadísticos de orden ( order statistics ). La medida más elemental es el rango ( range ): la diferencia entre los números de mayor y menor valor. Es de utilidad conocer los valores mínimos y máximos en sí, además de práctico, para identificar valores atípicos, pero el rango es extremadamente sensible a los valores atípicos y no es muy útil como medida general de la dispersión de datos.

Para evitar la sensibilidad a los valores atípicos, podemos observar el rango de los datos después de eliminar valores de cada extremo. Formalmente, este tipo de estimaciones se basan en diferencias entre percentiles ( percentiles ). En un conjunto de datos, el percentil P es un valor tal que al menos el P por ciento de los valores toman este valor o un valor inferior y al menos (100 - P ) por ciento de los valores toman este valor o un valor superior. Por ejemplo, para encontrar el percentil 80, ordenamos los datos. Luego, comenzando por el valor más pequeño, continuamos hasta el 80% del recorrido para llegar al mayor valor. Hay que tener en cuenta que la mediana es lo mismo que el percentil 50. El percentil es esencialmente lo mismo que el cuantil ( quantile ), con los cuantiles referenciados por porcentajes (por lo que el cuantil 0.8 es lo mismo que el percentil 80).