Peter Bruce - Estadística práctica para ciencia de datos con R y Python

A la mediana se le conoce como una estimación robusta ( robust ) de la localización, ya que no está influenciada por valores atípicos ( outliers ) (casos extremos) que podrían sesgar los resultados. Un valor atípico es cualquier valor que está muy lejos de los otros valores en el conjunto de datos. La definición exacta de valor atípico es algo subjetiva, a pesar de que se utilizan ciertas convenciones en distintos resúmenes de datos y diagramas (consultar "Percentiles y diagramas de caja" en la página 20). Ser un valor atípico en sí mismo no hace que un valor de los datos no sea válido o sea erróneo (como en el ejemplo anterior con Bill Gates). Aun así, los valores atípicos son a menudo el resultado de errores de datos, como la combinación de datos de diferentes unidades (kilómetros en lugar de metros) o las lecturas incorrectas de un sensor. Cuando los valores atípicos son el resultado de datos incorrectos, la media dará como resultado una estimación deficiente de la localización, mientras que la mediana seguirá siendo válida. Los valores atípicos deben identificarse y, por lo general, merecen una investigación más profunda.

En contraste con el análisis normal de datos, donde los valores atípicos son a veces informativos y a veces molestos, en la detección de anomalías ( anomaly detection ) los puntos que nos interesan son los valores atípicos, y la mayor masa de datos sirve principalmente para definir la "normalidad" con la que se miden las anomalías.

La mediana no es la única estimación robusta de la localización. De hecho, la media truncada se usa habitualmente para evitar la influencia de valores atípicos. Por ejemplo, truncar el 10% inferior y superior (una opción frecuente) de los datos proporcionará protección contra valores atípicos en todos los conjuntos de datos, excepto en los más pequeños. La media truncada se puede considerar un compromiso entre la mediana y la media: es robusta a los valores extremos de los datos, pero utiliza más datos para calcular la estimación de la localización.

Los estadísticos han desarrollado una plétora de otros estimadores de localización, principalmente con el objetivo de desarrollar un estimador más robusto que la media y también más eficiente (es decir, más capaz de discernir pequeñas diferencias de localización entre conjuntos de datos). Si bien estos métodos son potencialmente útiles para conjuntos de datos pequeños, no es probable que proporcionen algún beneficio adicional para conjuntos con cantidades grandes de datos o incluso de tamaño moderado.

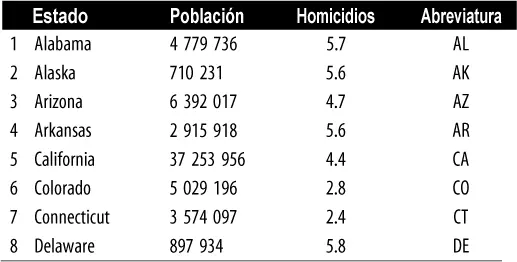
La tabla 1.2muestra las primeras filas del conjunto de datos que contienen la población y las tasas de homicidios (en unidades de homicidios por cada 100 000 habitantes y por año) para cada estado de EE. UU. (censo de 2010).

Tabla 1.2Algunas filas de data.frame de la situación de la población y la tasa de homicidios por estados

Utilizamos R para calcular la media, la media truncada y la mediana de la población:

Para calcular la media y la mediana con Python , podemos emplear los métodos pandas del marco de datos. La media truncada requiere la función trim_mean de scipy.stats:

La media es mayor que la media truncada, que es mayor que la mediana.

Esto se debe a que la media truncada excluye los cinco estados más grandes y más pequeños (trim=0.1 ignora el 10% de cada extremo). Si queremos calcular la tasa de homicidios promedio para el país, necesitamos usar una media o mediana ponderadas para dar cuenta de las diferentes poblaciones de los estados. Dado que el software básico de R no tiene una función para la mediana truncada, necesitamos instalar el paquete matrixStats:

Con NumPy podemos disponer de la media ponderada. Para la mediana ponderada, podemos usar el paquete especializado wquantiles ( https://pypi.org/project/wquantiles/ ):

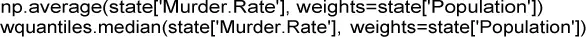
En este caso, la media ponderada y la mediana ponderada son aproximadamente iguales.

Ideas clave

• La métrica básica para la localización es la media, pero puede ser sensible a valores extremos (valores atípicos).

• Otras métricas (mediana, media truncada) son menos sensibles a valores atípicos y a distribuciones inusuales y, por lo tanto, son más robustas.

• El artículo de Wikipedia sobre tendencia central contiene un amplio debate sobre varias medidas de localización.

• El clásico Exploratory Data Analysis (Pearson) de John Tukey de 1977 todavía se lee bastante.

La localización es solo una dimensión para extraer el resumen de una característica. Una segunda dimensión, la variabilidad ( variability ), también conocida como dispersión ( dispersion ), mide el grado de agrupación o dispersión de los valores de los datos. En el corazón de la estadística se encuentra la variabilidad: hay que medirla, reducirla, distinguir la variabilidad aleatoria de la real, identificar las diversas fuentes de variabilidad real y tomar decisiones teniéndola en cuenta.

Términos clave de métricas de variabilidad

Desviaciones

Diferencias entre los valores observados y la estimación de la localización.

Sinónimos

errores, residuales

Varianza

Suma de los cuadrados de las desviaciones de la media al cuadrado y dividida por n – 1, donde n es el número de valores de datos.

Sinónimo

error cuadrático medio

Desviación estándar

Raíz cuadrada de la varianza.

Desviación media absoluta

Media de los valores absolutos de las desviaciones de la media.

Sinónimos

norma L1, norma Manhattan

Desviación absoluta mediana de la mediana

Mediana de los valores absolutos de las desviaciones de la mediana.

Rango