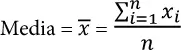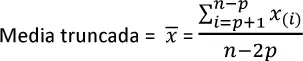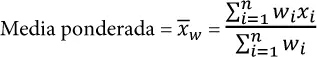Peter Bruce - Estadística práctica para ciencia de datos con R y Python

Media

Suma de todos los valores dividida por el número de valores.

Sinónimos

promedio

Media ponderada

Suma de todos los valores multiplicados por cada ponderación y dividida por la suma de las ponderaciones.

Sinónimo

promedio ponderado

Mediana

Valor tal que la mitad del número de datos se encuentra por encima y la otra mitad por debajo de dicho valor.

Sinónimo

Percentil 50

Percentil

Valor tal que el P por ciento de los datos se encuentra por debajo del mismo.

Sinónimo

cuantil

Mediana ponderada

Valor tal que la mitad de la suma de las ponderaciones se encuentra por encima y la otra mitad por debajo de los datos ordenados.

Media recortada

El promedio de todos los valores después de eliminar un número fijo de valores extremos.

Sinónimo

media truncada

Robusto

Insensible a valores extremos.

Sinónimo

resistente

Atípico

Valor de un dato que es muy diferente de la mayoría de los valores de datos.

Sinónimo

valor extremo

A primera vista, resumir los datos puede parecer bastante trivial: simplemente hay que extraer la media ( mean ) de los datos. De hecho, si bien la media es fácil de calcular y conveniente de usar, es posible que no siempre sea la mejor medida para representar un valor central. Por esta razón, los estadísticos han desarrollado y promovido varias estimaciones alternativas a la media.

Métricas y estimaciones

Los estadísticos a menudo utilizan el término estimación ( estimate ) para referirse a un valor calculado a partir de los datos disponibles, para establecer una distinción entre lo que vemos a partir de los datos y el verdadero estado teórico o exacto de las cosas. Es más probable que los científicos de datos y los analistas de negocios se refieran a este valor como métrica ( metric ). La diferencia refleja el enfoque de la estadística frente al de la ciencia de datos. Hay que tener en cuenta que la explicación de la incertidumbre se encuentra en el corazón de la disciplina de la estadística, mientras que el foco de la ciencia de datos son los objetivos concretos de las organizaciones o de las empresas. Por lo tanto, los estadísticos estiman y los científicos de datos miden.

La estimación más elemental para la localización es el valor medio o promedio ( average ). La media es la suma de todos los valores dividida por el número de valores. Consideremos el siguiente conjunto de números: {3 5 1 2}. La media es (3 + 5 + 1 +2) / 4 = 11/4 = 2.75. Nos encontraremos el símbolo x (pronunciado "barra x") que se utiliza para representar la media de la muestra de una población. La fórmula para calcular la media de un conjunto de n valores x 1, x 2, ..., x n es:

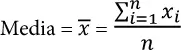
N (o n ) se refiere al número total de registros u observaciones. En estadística, se escribe con mayúscula si se refiere a una población y en minúscula si se refiere a una muestra de una población. En la ciencia de datos, esa distinción no es vital, por lo que se puede ver de las dos formas.

La variación de la media se conoce como media truncada ( trimmed mean ), que se calcula ignorando un número fijo, en cada extremo, de valores ordenados y a continuación se calcula el promedio de los valores restantes. Al representar los valores ordenados por x (1), x (2), ..., x (n)donde x (1)es el valor más pequeño y x (n)el valor más grande, la fórmula para calcular la media recortada con los p valores más pequeños y más grandes omitidos es:

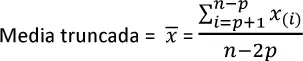
La media truncada elimina la influencia de valores extremos. Por ejemplo, en el buceo internacional, se eliminan las puntuaciones máxima y mínima de cinco jueces, y la puntuación final es el promedio de las puntuaciones de los tres jueces restantes ( https://en.wikipedia.org/wiki/Diving_(sport)#Scoring_the_dive ). Esto hace que sea difícil para un solo juez manipular la puntuación, tal vez para favorecer al concursante de su país. Las medias truncadas se utilizan habitualmente y, en muchos casos, son preferibles a la media ordinaria. En el apartado "Estimación de medianas robustas" de la página 10se amplía esta información.

Otro tipo de media es la media ponderada ( weighted mean ), que se calcula multiplicando cada valor de datos x i por el peso w i especificado por el usuario y dividiendo su suma por la suma de las ponderaciones. La fórmula para una media ponderada es:

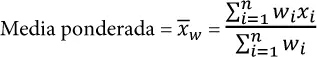
Hay dos motivos fundamentales para usar una media ponderada:

• Algunos valores son intrínsecamente más variables que otros, y las observaciones muy variables reciben un peso menor. Por ejemplo, si tomamos el promedio de varios sensores y uno de los sensores es menos preciso, entonces podríamos reducir la ponderación de los datos de ese sensor.

• Los datos recopilados no representan por igual a los diferentes grupos que nos interesa medir. Por ejemplo, debido a la forma en la que se ha realizado un experimento en línea, es posible que no tengamos un conjunto de datos que refleje con precisión todos los grupos en la base de datos de los usuarios. Para corregir eso, podemos dar un mayor peso a los valores de los grupos que tengan una menor representación.

La mediana ( median ) es el valor central de una lista de datos ordenados de menor a mayor. Si hay un número par de valores de datos, el valor medio es uno que no está realmente en el conjunto de datos, sino el promedio de los dos valores que dividen los datos ordenados en mitades superior e inferior. En comparación con la media, que utiliza todas las observaciones, la mediana depende solo de los valores situados en el centro de los datos ordenados. Si bien esto puede parecer una desventaja, dado que la media es mucho más sensible a los datos, hay muchos casos en los que la mediana es una mejor métrica para la localización. Supongamos que queremos analizar los ingresos familiares típicos en los vecindarios de los alrededores del lago Washington en Seattle. Al comparar el vecindario de Medina con el de Windermere, la utilización de la media produciría resultados muy diferentes porque Bill Gates vive en Medina. Si usamos la mediana, no importará lo rico que sea Bill Gates, porque la posición de la observación intermedia seguirá siendo la misma.

Por las mismas razones por las que se usa una media ponderada, también es posible calcular una mediana ponderada ( weighted median ). Al igual que con la mediana, primero ordenamos los datos, aunque cada valor de los datos tiene una ponderación asociada. En lugar del número del medio, la mediana ponderada es un valor tal que la suma de las ponderaciones es igual para las mitades inferior y superior de la lista ordenada. Como la mediana, la mediana ponderada es robusta a valores atípicos.