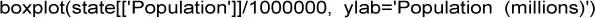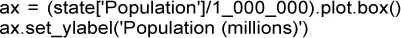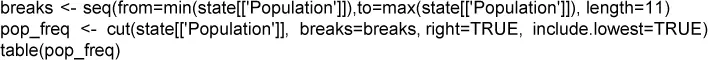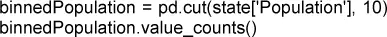Peter Bruce - Estadística práctica para ciencia de datos con R y Python

La mediana es de 4 homicidios por cada 100 000 habitantes, aunque hay bastante variabilidad: el percentil 5 es solo 1.6 y el percentil 95 es 6.51.

Los diagramas de caja ( boxplots ), presentados por Tukey [Tukey, 1977], utilizan percentiles y permiten visualizar la distribución de datos de una forma rápida. La figura 1.2muestra el diagrama de caja de la población por cada estado, que proporciona R :

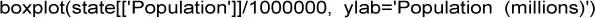
pandas proporciona una serie de gráficos exploratorios básicos para el marco de datos. Uno de ellos es el diagrama de caja:

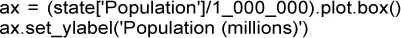
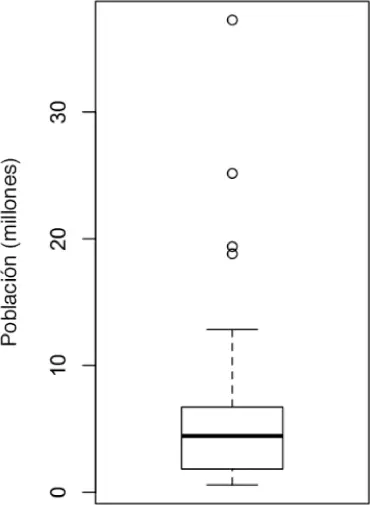
Figura 1.2 Diagrama de caja de la población por estados.

En este diagrama de caja, podemos ver de forma inmediata que la mediana de la población por estados es de alrededor de 5 millones, la mitad de los estados se encuentran entre aproximadamente 2 millones y 7 millones, y hay algunos valores atípicos de altos niveles de población. La parte superior e inferior del cuadro son los percentiles 75 y 25, respectivamente. La mediana se muestra mediante una línea horizontal dentro del cuadro. Las líneas discontinuas, denominadas bigotes ( whiskers ), se extienden desde las partes superior e inferior del cuadro para indicar el rango de la mayor parte de los datos. Hay muchas variaciones del diagrama de caja. Ver, por ejemplo, la documentación de la función boxplot de R [R-base, 2015]. Por defecto, la función R extiende los bigotes hasta el punto más alejado fuera de la caja, pero no van más allá de 1.5 veces el IQR. Matplotlib utiliza la misma implementación. Cualquier otro software puede usar una regla diferente.

Los datos que aparecen fuera de los bigotes se representan como puntos o círculos (a menudo considerados valores atípicos).

La tabla de frecuencias de una variable divide el rango de la variable en segmentos igualmente espaciados y nos dice cuántos valores caen dentro de cada segmento. La tabla 1.5muestra la tabla de frecuencias de la población por cada estado calculada mediante R :

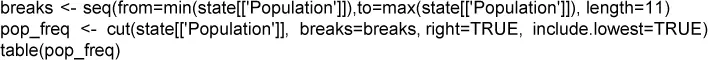
La función pandas.cut crea una serie que asigna los valores a los segmentos. Mediante el método value_counts, obtenemos la tabla de frecuencias:

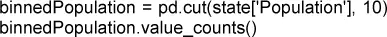
Tabla 1.5Tabla de frecuencias de la población por estados

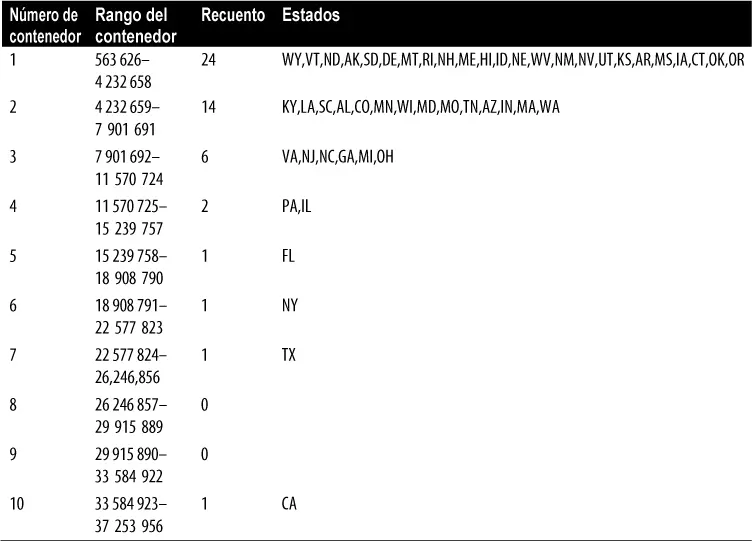
El estado menos poblado es Wyoming, con 563 626 habitantes, y el más poblado es California, con 37 253 956 habitantes. Esto nos da un rango de 37 253 956 – 563 626 = 36 690 330, que debemos dividir en contenedores de igual tamaño, digamos 10 contenedores. Con 10 contenedores del mismo tamaño, cada contenedor tendrá una anchura de 3 669 033, por lo que el primer contenedor incluirá desde 563 626 a 4 232 658. Por el contrario, el contenedor superior, desde 33 584 923 a 37 253 956, tiene un solo estado: California. Los dos contenedores inmediatamente por debajo del de California están vacíos, hasta llegar a Texas. Es importante incluir los contenedores vacíos. El hecho de que no haya valores en esos contenedores constituye una información valiosa. También puede resultar conveniente experimentar con distintos tamaños de contenedores. Si son demasiado grandes, se pueden ocultar características importantes de la distribución. Si son demasiado pequeños, el resultado es demasiado granular y se pierde la capacidad de ver el panorama general.

Tanto las tablas de frecuencias como los percentiles, extraen el resumen de los datos mediante la creación de contenedores. En general, los cuartiles y deciles tendrán el mismo número de valores en cada contenedor (contenedores de igual número de valores), pero los tamaños de los contenedores serán diferentes. La tabla de frecuencias, por el contrario, tendrá diferente número de valores en los contenedores (contenedores de igual tamaño) y el tamaño de los contenedores será el mismo para todos.

El histograma es un modo de visualizar la tabla de frecuencias, con contenedores en el eje x y los valores de los datos en el eje y. En la figura 1.3, por ejemplo, el contenedor centrado en 10 millones (1e + 07) va de aproximadamente 8 millones a 12 millones, y hay seis estados en ese contenedor. Para crear mediante R el histograma correspondiente a la tabla 1.5, utilizamos la función hist con el argumento breaks:

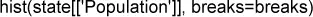
pandas soporta histogramas para marcos de datos con el método DataFrame.plot.hist. Utilizamos el argumento de palabra clave bins para definir el número de contenedores. Los diversos métodos de diagramas proporcionan como resultado un eje de objetos que permite mejorar el ajuste de la visualización mediante Matplotlib:

El histograma se muestra en la figura 1.3. En general, los histogramas se representan gráficamente teniendo en cuenta que:

• Los contenedores vacíos se incluyen en el gráfico.

• Los contenedores tienen la misma anchura.

• El número de contenedores (o, de manera equivalente, el tamaño del contenedor) depende del usuario.

• Las barras son contiguas: no se muestran espacios vacíos entre las barras, a menos que haya un contenedor vacío.

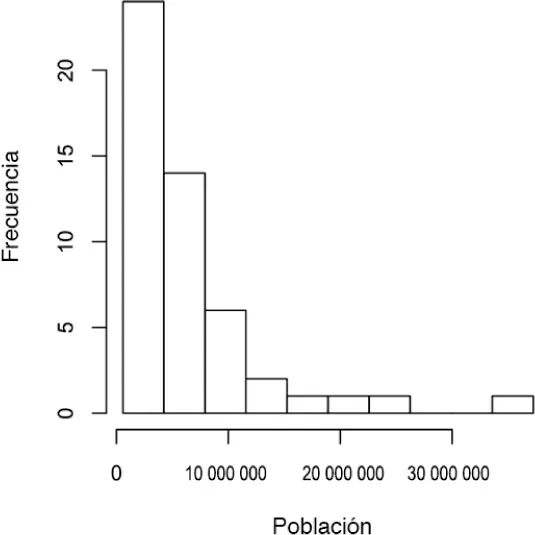
Figura 1.3 Histograma de población por estados.

En teoría estadística, la localización y la variabilidad se conocen como el primer y segundo momentos ( moments ) de una distribución. Los momentos tercero y cuarto se denominan asimetría ( skewness ) y curtosis ( kurtosis ). La asimetría se refiere a si los datos están sesgados hacia valores mayores o menores, y la curtosis indica la propensión de los datos a tener valores extremos. Generalmente, no se utilizan métricas para medir la asimetría y la curtosis, sino que se descubren a través de presentaciones visuales como las figuras 1.2y 1.3.