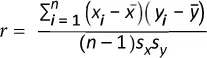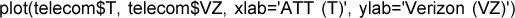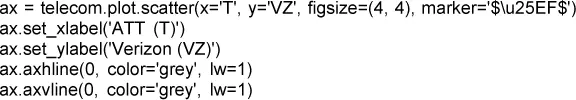Peter Bruce - Estadística práctica para ciencia de datos con R y Python

Más útil es una variante estandarizada: el coeficiente de correlación ( correlation coefficient ), que proporciona una estimación de la correlación entre dos variables que siempre tienen la misma escala. Para calcular el coeficiente de correlación de Pearson ( Pearson’s correlation coefficient ), multiplicamos las desviaciones de la media de la variable 1 por las de la variable 2 y las dividimos por el producto de las desviaciones estándar:

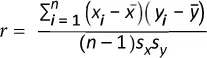
Hay que tener en cuenta que dividimos por n – 1 en lugar de n . Consultar "Grados de libertad, y ¿n o n – 1?" en la página 15para ampliar detalles. El coeficiente de correlación siempre se encuentra entre +1 (correlación positiva perfecta) y –1 (correlación negativa perfecta). El 0 indica que no hay correlación.

Las variables pueden tener una asociación no lineal, en cuyo caso el coeficiente de correlación puede no ser una métrica útil. La relación entre las tasas impositivas y los ingresos recaudados es un ejemplo: a medida que las tasas impositivas aumentan desde cero, los ingresos recaudados también aumentan. Sin embargo, una vez que las tasas impositivas alcanzan un nivel alto y se acercan al 100%, la evasión fiscal aumenta y los ingresos fiscales en realidad disminuyen.

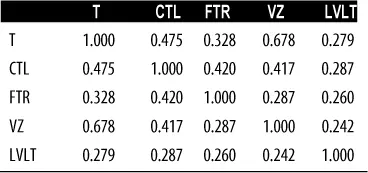
La tabla 1.7, denominada matriz de correlación ( correlation matrix ), muestra la correlación entre las rentabilidades diarias de las acciones de telecomunicaciones desde julio de 2012 hasta junio de 2015. En la tabla, podemos ver que Verizon (VZ) y ATT (T) tienen la correlación más alta. Level 3 (LVLT), que es una empresa de infraestructuras, tiene la correlación más baja con las demás. Hay que tener en cuenta la diagonal de 1s (la correlación de una acción consigo misma es 1) y la redundancia de la información por encima y por debajo de la diagonal.

Tabla 1.7Correlación entre la rentabilidad de las acciones de telecomunicaciones

Por lo general, se presenta una tabla de correlaciones como la tabla 1.7para mostrar visualmente la relación entre múltiples variables. La figura 1.6muestra la correlación entre las rentabilidades diarias de los principales fondos cotizados en bolsa (ETF). En R , podemos crear esta figura fácilmente usando el paquete corrplot:

Es posible crear el mismo gráfico con Python , pero no hay ninguna implementación en los paquetes convencionales. Sin embargo, la mayoría soporta la visualización de matrices de correlación mediante mapas de calor. El siguiente código lo realiza haciendo uso del paquete seaborn.heat map. En el repositorio de código fuente adjunto, incluimos código Python para generar una visualización más completa:

Los ETF para el S&P 500 (SPY) y el Índice Dow Jones (DIA) tienen una alta correlación. Del mismo modo, el QQQ y el XLK, compuestos en su mayoría por empresas de tecnología, están correlacionados positivamente. Los ETF defensivos, como los que rastrean los precios del oro (GLD), los precios del petróleo (USO) o la volatilidad del mercado (VXX), tienden a tener una correlación débil o negativa con los otros ETF. La orientación de la elipse indica si dos variables están correlacionadas positivamente (la elipse apunta hacia la parte superior derecha) o correlacionados negativamente (la elipse apunta hacia la parte superior izquierda). El sombreado y la anchura de la elipse indican la fuerza de la asociación: las elipses más delgadas y más oscuras corresponden a relaciones más fuertes ( figura 1.6).

Figura 1.6 Correlación entre rentabilidades de ETF.

Al igual que la media y la desviación estándar, el coeficiente de correlación es sensible a valores extremos en los datos. Los paquetes de software ofrecen alternativas robustas al coeficiente de correlación clásico. Por ejemplo, el paquete robust de R ( https://cran.rproject.org/web/packages/robust/robust.pdf ) utiliza la función covRob para calcular una estimación robusta de correlación. Los métodos sklearn.covariance ( https://scikitlearn.org/stable/modules/classes.html#module-sklearn.covariance ) del módulo scikitlearn implementan diversos enfoques.

Los estadísticos propusieron hace mucho tiempo otros tipos de coeficientes de correlación, como rho de Spearman o tau de Kendall . Estos son coeficientes de correlación basados en el rango de los datos. Dado que trabajan con rangos en lugar de valores, estas estimaciones son robustas a valores atípicos y pueden manejar ciertos tipos de falta de linealidad. Sin embargo, los científicos de datos generalmente pueden ceñirse al coeficiente de correlación de Pearson y sus alternativas robustas para el análisis exploratorio. Las estimaciones basadas en rangos son atractivas principalmente para conjuntos de datos más pequeños y pruebas de hipótesis específicas.

La forma tradicional de visualizar la relación entre dos variables de datos que hemos registrado es con un diagrama de dispersión. En el eje x se representa una variable y en el eje y otra, y cada punto del gráfico es un registro. En la figura 1.7se muestra un gráfico de la correlación entre las rentabilidades diarias de ATT y Verizon. La visualización se consigue en R con el comando:

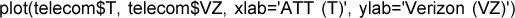
El mismo gráfico se puede generar en Python usando el método de dispersión de pandas:

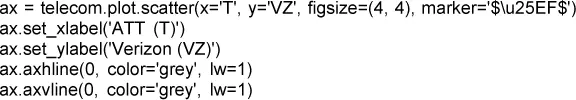
Las rentabilidades tienen una relación positiva: mientras se agrupan alrededor del cero, la mayor parte de los días, las acciones suben o bajan conjuntamente (cuadrantes superior derecho e inferior izquierdo). Hay menos días en los que una acción baja significativamente mientras que la otra sube, o viceversa (cuadrantes inferior derecho y superior izquierdo).

Si bien el diagrama de la figura 1.7muestra solo 754 puntos de datos, ya es obvio lo difícil que es identificar detalles en el centro del diagrama. Más adelante veremos cómo la adición de transparencia a los puntos, o el uso de agrupaciones hexagonales y diagramas de densidad, puede ayudar a encontrar una estructura complementaria en los datos.