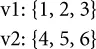Peter Bruce - Estadística práctica para ciencia de datos con R y Python

Hay que tener en cuenta que un gráfico de barras se parece a un histograma. En un gráfico de barras, el eje x representa diferentes categorías de una variable de tipo factor, mientras que, en un histograma, el eje x representa los valores de una sola variable en una escala numérica. En un histograma, las barras generalmente se muestran tocándose entre sí. Si hay espacios, estos indican valores ausentes en los datos. En un gráfico de barras, las barras se muestran separadas entre sí.

Los gráficos en forma de tarta son una alternativa a los gráficos de barras, aunque los estadísticos y los expertos en visualización de datos generalmente evitan los gráficos en forma de tarta por ser menos informativos visualmente (ver [Few, 2007]).

En "Tablas de frecuencias e histogramas" en la página 22, analizamos las tablas de frecuencias basadas en la agrupación de datos. Esta acción convierte implícitamente los datos numéricos en un factor ordenado. En este sentido, los histogramas y los gráficos de barras son similares, excepto que las categorías del eje x en el gráfico de barras no están ordenadas. La conversión de datos numéricos en datos categóricos es un paso importante y se utiliza de forma generalizada en el análisis de datos, ya que reduce la complejidad (y el tamaño) de los datos. Esto ayuda a descubrir las relaciones entre las características, particularmente en las etapas iniciales del análisis.

La moda es el valor (o valores en caso de empate) que aparece con mayor frecuencia en los datos. Por ejemplo, la moda de la causa de los retrasos en el aeropuerto de Dallas/Fort Worth es "Inbound" (llegadas). Por citar otro ejemplo, en la mayor parte de Estados Unidos, la moda de la preferencia religiosa sería el cristianismo. La moda es un resumen estadístico simple para datos categóricos y, por lo general, no se utiliza para datos numéricos.

Un tipo especial de datos categóricos son los datos en los que las categorías representan o pueden asignarse a valores discretos en la misma escala. Un vendedor de una nueva tecnología en la nube, por ejemplo, ofrece dos niveles de servicio, uno con un precio de 300 $ al mes y otro de 50 $ al mes. Este especialista en marketing ofrece seminarios web gratuitos para generar potenciales clientes, y la firma calcula que el 5% de los asistentes se inscribirá en el servicio de 300 $, el 15% se inscribirá en el servicio de 50 $ y el 80% no se inscribirá en nada. Estos datos se pueden resumir, con fines de tipo financiero, en un solo "valor esperado", que es una forma de media ponderada, en la que las ponderaciones son probabilidades.

El valor esperado se calcula de la siguiente manera:

1. Multiplicamos cada resultado por la probabilidad de que ocurra.

2. Sumamos esos valores.

En el ejemplo del servicio en la nube, el valor esperado de un asistente a un seminario web es, por lo tanto, de 22.50 $ al mes, calculado de la siguiente manera:

EV = (0.05)(300) + (0.15)(50) + (0.80)(0) = 22.5

El valor esperado es realmente una forma de media ponderada: suma las ideas de expectativas futuras y las ponderaciones de probabilidad, a menudo basadas en juicios subjetivos. El valor esperado es un concepto fundamental en la valoración de empresas y en los presupuestos de capital, por ejemplo, el valor esperado de los beneficios a los cinco años de una nueva adquisición, o los ahorros de costes esperados de un nuevo software de administración de pacientes de una clínica.

Nos referimos anteriormente a la probabilidad ( probability ) de que ocurra un valor. La mayoría de las personas tiene una comprensión intuitiva de la probabilidad, y se encuentran con frecuencia con este concepto en los pronósticos meteorológicos (la probabilidad de que llueva) o en el análisis deportivo (la probabilidad de ganar). Los deportes y los juegos se expresan más a menudo como oportunidades, que se pueden convertir fácilmente en probabilidades (si las oportunidades de que un equipo gane son de 2 a 1, su probabilidad de ganar es 2 / (2 + 1) = 2/3). Sin embargo, sorprendentemente, el concepto de probabilidad puede ser motivo de una profunda discusión filosófica a la hora de definirlo. Afortunadamente, aquí no necesitamos una definición matemática o filosófica formal. Para nuestros propósitos, la probabilidad de que suceda un evento es la proporción de veces que ocurriría si la situación pudiera repetirse una y otra vez, innumerables veces. La mayoría de las ocasiones se trata de una construcción imaginaria, pero es una comprensión funcional adecuada de la probabilidad.

Ideas clave

• Los datos categóricos generalmente se resumen en porcentajes y se pueden visualizar en un gráfico de barras.

• Las categorías pueden representar diferentes cosas (manzanas y naranjas, hombres y mujeres), niveles de una variable de tipo factor (bajo, medio y alto) o datos numéricos que se han agrupado.

• El valor esperado es la suma de los valores multiplicados por las probabilidades de que ocurran. A menudo se usa para totalizar los niveles de las variables de tipo factor.

Ningún curso de estadística está completo sin una lección sobre gráficos que inducen a error ( https://en.wikipedia.org/wiki/Misleading_graph ), que a menudo incluyen gráficos de barras y gráficos en forma de tarta.

El análisis exploratorio de datos en muchos proyectos de modelado (ya sea en ciencia de datos o en investigación) implica examinar la correlación entre predictoras y entre predictoras y una variable objetivo. Se dice que las variables X e Y (cada una con datos registrados) están correlacionadas positivamente si los valores altos de X acompañan a los valores altos de Y, y los valores bajos de X acompañan a los valores bajos de Y. Si los valores altos de X acompañan a los valores bajos de Y, y viceversa, las variables están correlacionadas negativamente.

Términos clave de la correlación

Coeficiente de correlación

Métrica que mide el grado en que las variables numéricas están asociadas entre sí (varía de –1 a +1).

Matriz de correlación

Tabla en la que las variables se muestran tanto en filas como en columnas, y los valores de las celdas son las correlaciones entre las variables.

Diagrama de dispersión

Diagrama en el que el eje x es el valor de una variable y el eje y es el valor de otra.

Consideremos estas dos variables, perfectamente correlacionadas en el sentido de que cada una va de menor a mayor:

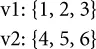
La suma vectorial de los productos es 1 · 4 + 2 · 5 + 3 · 6 = 32. Ahora intentemos barajar una de ellas y volvamos a hacer el cálculo. La suma vectorial de productos nunca será mayor que 32. Por lo tanto, esta suma de productos podría utilizarse como métrica. Es decir, la suma observada de 32 podría compararse con muchas mezclas aleatorias (de hecho, esta idea se relaciona con una estimación basada en el remuestreo. Consultar "Prueba de permutación" en la página 97). Sin embargo, los valores generados por esta métrica no son tan importantes, excepto en lo referente a la distribución del remuestreo.