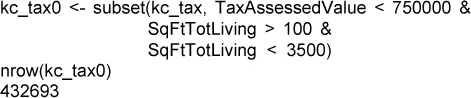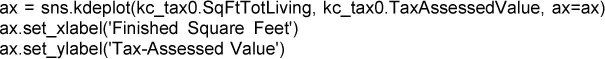Peter Bruce - Estadística práctica para ciencia de datos con R y Python

Figura 1.7 Diagrama de dispersión de la correlación entre las rentabilidades de ATT y Verizon.

Ideas clave

• El coeficiente de correlación mide el grado en que dos variables emparejadas (por ejemplo, la altura y el peso de los individuos) están asociadas entre sí.

• Cuando los valores altos de v1 acompañan a los valores altos de v2, v1 y v2 se asocian positivamente.

• Cuando los valores altos de v1 acompañan a los valores bajos de v2, v1 y v2 se asocian negativamente.

• El coeficiente de correlación es una métrica estandarizada, por lo que siempre varía de –1 (correlación negativa perfecta) a +1 (correlación positiva perfecta).

• Un coeficiente de correlación de cero indica que no hay correlación, pero hay que tener en cuenta que las disposiciones aleatorias de datos producirán valores tanto positivos como negativos para el coeficiente de correlación simplemente por casualidad.

Statistics , 4. aed., de David Freedman, Robert Pisani y Roger Purves (W. W. Norton, 2007) contiene una excelente discusión sobre correlación.

Los estimadores habituales como la media y la varianza analizan las variables una por una ( análisis univariable [ univariate analysis ]). El análisis de correlación (consultar "Correlación" en la página 30) es un método importante que compara dos variables ( análisis bivariable [ bivariate analysis ]). En esta sección, analizamos estimaciones y diagramas complementarios aplicados a más de dos variables ( análisis multivariante [ multivariate analysis ]).

Términos clave de la exploración de dos o más variables

Tabla de contingencia

Registro del recuento entre dos o más variables categóricas.

Agrupación hexagonal

Diagrama de dos variables numéricas con los registros agrupados en hexágonos.

Diagrama de contorno

Diagrama que muestra la densidad de dos variables numéricas en forma de mapa topográfico.

Diagrama de violín

Similar a un diagrama de caja pero en el que se muestra la densidad estimada.

Al igual que el análisis univariable, el análisis bivariable implica tanto el cálculo de estadísticos de resumen como la generación de presentaciones visuales. El tipo apropiado de análisis bivariable o multivariable depende de la naturaleza de los datos: numéricos frente a categóricos.

Los diagramas de dispersión son apropiados cuando hay un número relativamente pequeño de valores de datos. La gráfica de las rentabilidades de las acciones en la figura 1.7solo involucra aproximadamente a 750 puntos. Para conjuntos de datos con cientos de miles o millones de registros, un diagrama de dispersión será demasiado denso, por lo que necesitamos visualizar la relación de un modo diferente. Para ilustrarlo, consideremos el conjunto de datos kc_tax, que contiene los valores tasados por impuestos para propiedades residenciales en el condado de King, Washington. Para centrarnos en la parte principal de los datos, eliminamos las residencias muy caras y muy pequeñas o muy grandes utilizando la función subset:

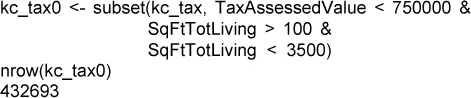
En pandas, filtramos el conjunto de datos de la siguiente manera:

La figura 1.8es un diagrama de agrupación hexagonal ( hexagonal binning ) de la relación entre la superficie terminada en pies cuadrados y el valor tasado por impuestos para las viviendas en el condado de King. En lugar de trazar puntos, que aparecerían como una nube oscura monolítica, agrupamos los registros en contenedores hexagonales y rellenamos los hexágonos con un color que indica el número de registros en ese contenedor. En este gráfico, la relación positiva entre los pies cuadrados y el valor de tasación fiscal es clara. Una característica interesante es que se muestran ligeramente bandas adicionales por encima de la banda principal (la más oscura) en la parte inferior, que indica los hogares que tienen la misma superficie en pies cuadrados que los de la banda principal pero un valor fiscal más alto.

La figura 1.8la ha generado el potente paquete de R ggplot2, desarrollado por Hadley Wickham [ggplot2]. ggplot2 es una de las múltiples nuevas bibliotecas de software para el análisis visual exploratorio avanzado de datos. Consultar "Visualización de varias variables" en la página 43:

En Python , se puede disponer fácilmente de los diagramas de agrupación hexagonal utilizando el método hexbin del marco de datos de pandas:

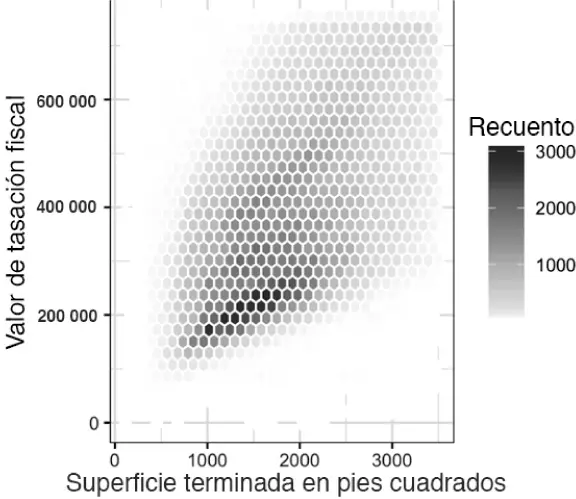
Figura 1.8 Agrupación hexagonal para el valor de tasación fiscal en relación con la superficie terminada en pies cuadrados.

La figura 1.9utiliza contornos superpuestos a un diagrama de dispersión para visualizar la relación entre dos variables numéricas. Los contornos son esencialmente un mapa topográfico con dos variables. Cada banda de contorno representa una densidad específica de puntos, que aumenta a medida que nos acercamos a un "pico". Este gráfico muestra una historia similar a la de la figura 1.8: hay un pico secundario "al norte" del pico principal. Este cuadro también se ha creado mediante ggplot2 con la función incorporada geom_density2d:

La función seaborn kdeplot de Python crea la gráfica de contorno:

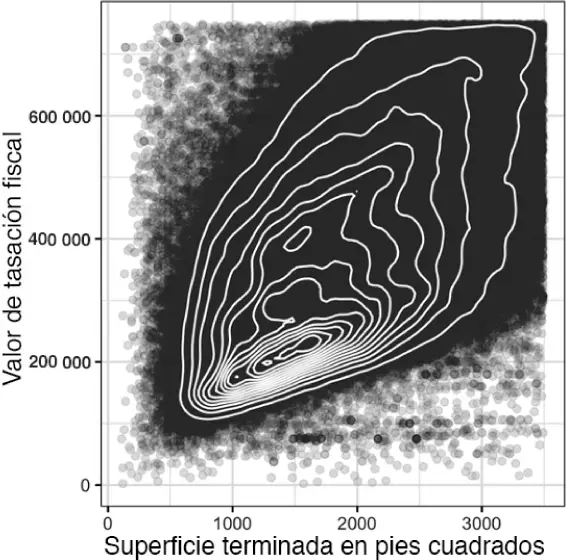
Figura 1.9 Gráfico de contorno para el valor de tasación fiscal en relación con la superficie terminada en pies cuadrados.

Se utilizan otros tipos de gráficos para mostrar la relación entre dos variables numéricas, incluidos los mapas de calor ( heat maps ). Los mapas de calor, la agrupación hexagonal y los gráficos de contorno proporcionan una representación visual bidimensional de la densidad. En este sentido, son por su naturaleza semejantes a los histogramas y diagramas de densidad.