1 ...6 7 8 10 11 12 ...22 From its structure, it is obvious that the observability Gramian matrix is symmetric and nonnegative. If we apply a transformation, 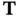 , to the state vector,
, to the state vector, 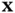 , such that
, such that 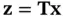 , the output energy:
, the output energy:
(2.47) 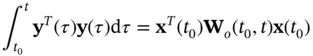
can be rewritten as:
(2.48) 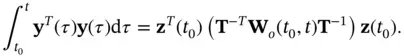
If the transformation 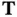 is chosen in a way that the transformed observability Gramian matrix,
is chosen in a way that the transformed observability Gramian matrix, 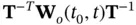 , is diagonal, then, its diagonal elements can be viewed as the contribution of different state variables in the initial state vector
, is diagonal, then, its diagonal elements can be viewed as the contribution of different state variables in the initial state vector 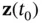 to the energy of the output. The continuous‐time LTV system of ( 2.36) and ( 2.37) is observable, if and only if the observability Gramian matrix
to the energy of the output. The continuous‐time LTV system of ( 2.36) and ( 2.37) is observable, if and only if the observability Gramian matrix 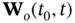 is nonsingular [9, 14].
is nonsingular [9, 14].
2.5.2 Discrete‐Time LTV Systems
The state‐space model of a discrete‐time LTV system is represented by the following algebraic and difference equations:
(2.49) 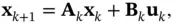
(2.50) 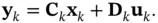
Before proceeding with a discussion on the observability condition, we need to define the discrete‐time state‐transition matrix , 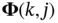 , as the solution of the following difference equation:
, as the solution of the following difference equation:
(2.51) 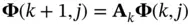
with the initial condition:
(2.52) 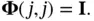
The reason that 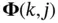 is called the state‐transition matrix is that it describes the dynamic behavior of the following autonomous system (a system with no input):
is called the state‐transition matrix is that it describes the dynamic behavior of the following autonomous system (a system with no input):
(2.53) 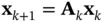
with 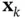 being obtained from
being obtained from
(2.54) 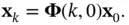
Following a discussion on energy of the system output similar to the continuous‐time case, we reach the following definition for the discrete‐time observability Gramian matrix:
(2.55) 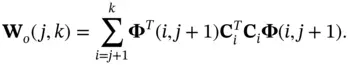
As before, the system ( 2.49) and ( 2.50) is observable, if and only if the observability Gramian matrix 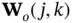 is full‐rank (nonsingular) [9].
is full‐rank (nonsingular) [9].
2.5.3 Discretization of LTV Systems
This section generalizes the method presented before for discretization of continuous‐time LTI systems and describes how the continuous‐time LTV system ( 2.36) and ( 2.37) can be discretized. Solving the differential equation in ( 2.36), we obtain:
(2.56) 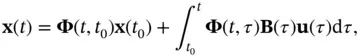
where 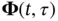 is the state‐transition matrix as described in ( 2.40) and ( 2.41). Using zero‐order‐hold sampling results in a piecewise‐constant input
is the state‐transition matrix as described in ( 2.40) and ( 2.41). Using zero‐order‐hold sampling results in a piecewise‐constant input 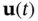 , which remains constant at
, which remains constant at 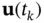 over the time interval
over the time interval 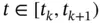 . Setting
. Setting 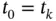 and
and 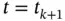 , from ( 2.56), we will have:
, from ( 2.56), we will have:
(2.57) 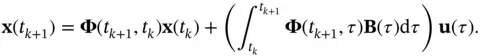
Therefore, dynamics of the discrete‐time equivalent of the continuous‐time system in ( 2.36) and ( 2.37) will be governed by the following state‐space model [19]:
(2.58) 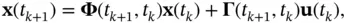
(2.59) 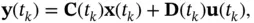
where
(2.60) 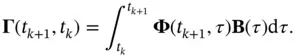
2.6 Observability of Nonlinear Systems
As mentioned before, observability is a global property for linear systems. However, for nonlinear systems, a weaker form of observability is defined, in which an initial state must be distinguishable only from its neighboring points. Two states 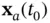 and
and 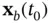 are indistinguishable , if their corresponding outputs are equal:
are indistinguishable , if their corresponding outputs are equal: 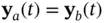 for
for 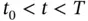 , where
, where  is finite. If the set of states in the neighborhood of a particular initial state
is finite. If the set of states in the neighborhood of a particular initial state 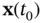 that are indistinguishable from it includes only
that are indistinguishable from it includes only 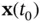 , then, the nonlinear system is said to be weakly observable at that initial state. A nonlinear system is called to be weakly observable if it is weakly observable at all
, then, the nonlinear system is said to be weakly observable at that initial state. A nonlinear system is called to be weakly observable if it is weakly observable at all 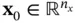 . If the state and the output trajectories of a weakly observable nonlinear system remain close to the corresponding initial conditions, then the system that satisfies this additional constraint is called locally weakly observable [13, 20].
. If the state and the output trajectories of a weakly observable nonlinear system remain close to the corresponding initial conditions, then the system that satisfies this additional constraint is called locally weakly observable [13, 20].
Читать дальше

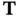 , to the state vector,
, to the state vector, 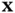 , such that
, such that 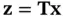 , the output energy:
, the output energy: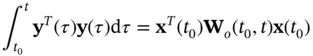
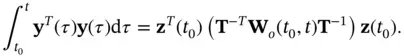
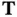 is chosen in a way that the transformed observability Gramian matrix,
is chosen in a way that the transformed observability Gramian matrix, 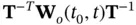 , is diagonal, then, its diagonal elements can be viewed as the contribution of different state variables in the initial state vector
, is diagonal, then, its diagonal elements can be viewed as the contribution of different state variables in the initial state vector 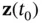 to the energy of the output. The continuous‐time LTV system of ( 2.36) and ( 2.37) is observable, if and only if the observability Gramian matrix
to the energy of the output. The continuous‐time LTV system of ( 2.36) and ( 2.37) is observable, if and only if the observability Gramian matrix 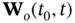 is nonsingular [9, 14].
is nonsingular [9, 14].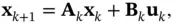
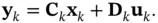
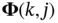 , as the solution of the following difference equation:
, as the solution of the following difference equation: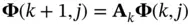
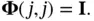
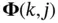 is called the state‐transition matrix is that it describes the dynamic behavior of the following autonomous system (a system with no input):
is called the state‐transition matrix is that it describes the dynamic behavior of the following autonomous system (a system with no input):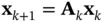
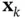 being obtained from
being obtained from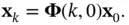
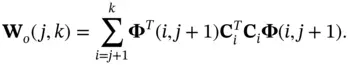
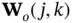 is full‐rank (nonsingular) [9].
is full‐rank (nonsingular) [9].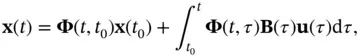
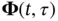 is the state‐transition matrix as described in ( 2.40) and ( 2.41). Using zero‐order‐hold sampling results in a piecewise‐constant input
is the state‐transition matrix as described in ( 2.40) and ( 2.41). Using zero‐order‐hold sampling results in a piecewise‐constant input 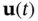 , which remains constant at
, which remains constant at 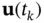 over the time interval
over the time interval 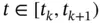 . Setting
. Setting 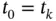 and
and 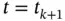 , from ( 2.56), we will have:
, from ( 2.56), we will have: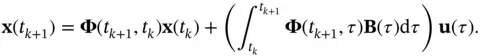
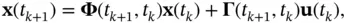
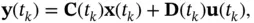
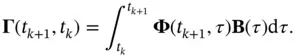
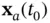 and
and 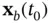 are indistinguishable , if their corresponding outputs are equal:
are indistinguishable , if their corresponding outputs are equal: 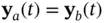 for
for 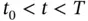 , where
, where  is finite. If the set of states in the neighborhood of a particular initial state
is finite. If the set of states in the neighborhood of a particular initial state 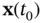 that are indistinguishable from it includes only
that are indistinguishable from it includes only 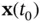 , then, the nonlinear system is said to be weakly observable at that initial state. A nonlinear system is called to be weakly observable if it is weakly observable at all
, then, the nonlinear system is said to be weakly observable at that initial state. A nonlinear system is called to be weakly observable if it is weakly observable at all 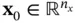 . If the state and the output trajectories of a weakly observable nonlinear system remain close to the corresponding initial conditions, then the system that satisfies this additional constraint is called locally weakly observable [13, 20].
. If the state and the output trajectories of a weakly observable nonlinear system remain close to the corresponding initial conditions, then the system that satisfies this additional constraint is called locally weakly observable [13, 20].










