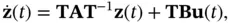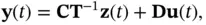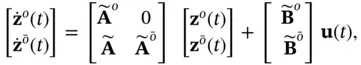Definition 2.1 (State observability) A dynamic system is state observable if for any time , the initial state can be uniquely determined from the time history of the input and the output for ; otherwise, the system is unobservable.
Unlike linear systems, there is not a universal definition for observability of nonlinear systems. Hence, different definitions have been proposed in the literature, which take two questions into consideration:
How to check the observability of a nonlinear system?
How to design an observer for such a system?
While for linear systems, observability is a global property, for nonlinear systems, observability is usually studied locally [9].
Definition 2.2 (State detectability) If all unstable modes of a system are observable, then the system is state detectable.
A system with undetectable modes is said to have hidden unstable modes [16, 17]. Sections provide observability tests for different classes of systems, whether they be linear or nonlinear, continuous‐time or discrete‐time.
2.4 Observability of Linear Time‐Invariant Systems
If the system matrices in the state‐space model of a linear system are constant, then, the model represents a linear time‐invariant (LTI) system.
2.4.1 Continuous‐Time LTI Systems
The state‐space model of a continuous‐time LTI system is represented by the following algebraic and differential equations:
(2.3)
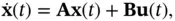
(2.4) 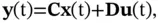
where  ,
,  , and
, and  are the state, the input, and the output vectors, respectively, and
are the state, the input, and the output vectors, respectively, and 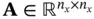 ,
, 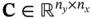 ,
,  , and
, and 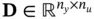 are the system matrices. Here, we need to find out when an initial state vector
are the system matrices. Here, we need to find out when an initial state vector 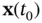 can be uniquely reconstructed from nonzero initial system output vector and its successive derivatives. We start by writing the system output vector and its successive derivatives based on the state vector as well as the input vector and its successive derivatives as follows:
can be uniquely reconstructed from nonzero initial system output vector and its successive derivatives. We start by writing the system output vector and its successive derivatives based on the state vector as well as the input vector and its successive derivatives as follows:
(2.5) 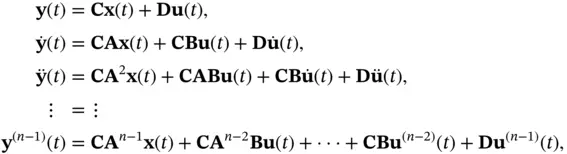
where the superscript in the parentheses denotes the order of the derivative. The aforementioned equations can be rewritten in the following compact form:
(2.6) 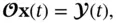
where
(2.7) 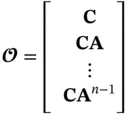
and
(2.8) 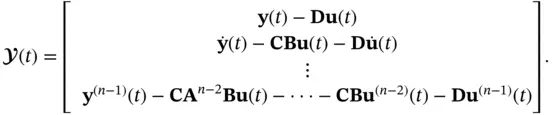
Initially we have
(2.9) 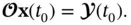
The continuous‐time system is observable, if and only if the observability matrix  is nonsingular (it is full rank), therefore the initial state can be found as:
is nonsingular (it is full rank), therefore the initial state can be found as:
(2.10) 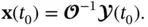
The observable subspace of the linear system, denoted by 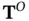 , is composed of the basis vectors of the range of
, is composed of the basis vectors of the range of 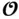 , and the unobservable subspace of the linear system, denoted by
, and the unobservable subspace of the linear system, denoted by 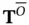 , is composed of the basis vectors of the null space of
, is composed of the basis vectors of the null space of 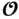 . These two subspaces can be combined to form the following nonsingular transformation matrix:
. These two subspaces can be combined to form the following nonsingular transformation matrix:
(2.11) 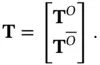
If we apply the aforementioned transformation to the state vector 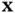 such that:
such that:
(2.12) 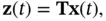
the transformed state vector 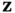 will be partitioned to observable modes,
will be partitioned to observable modes, 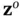 , and unobservable modes,
, and unobservable modes, 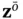 :
:
(2.13) 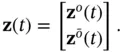
Then, the state‐space model of ( 2.3) and ( 2.4) can be rewritten based on the transformed state vector, 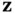 , as follows:
, as follows:
(2.14) 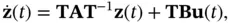
(2.15) 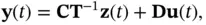
or equivalently as:
(2.16) 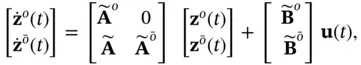
Читать дальше

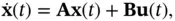
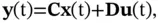
 ,
,  , and
, and  are the state, the input, and the output vectors, respectively, and
are the state, the input, and the output vectors, respectively, and 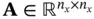 ,
, 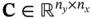 ,
,  , and
, and 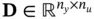 are the system matrices. Here, we need to find out when an initial state vector
are the system matrices. Here, we need to find out when an initial state vector 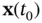 can be uniquely reconstructed from nonzero initial system output vector and its successive derivatives. We start by writing the system output vector and its successive derivatives based on the state vector as well as the input vector and its successive derivatives as follows:
can be uniquely reconstructed from nonzero initial system output vector and its successive derivatives. We start by writing the system output vector and its successive derivatives based on the state vector as well as the input vector and its successive derivatives as follows: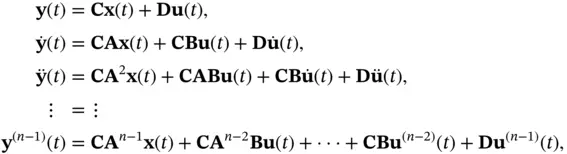
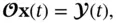

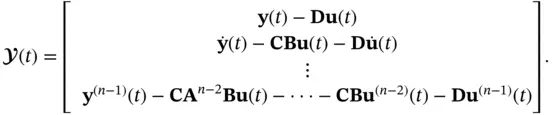
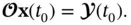
 is nonsingular (it is full rank), therefore the initial state can be found as:
is nonsingular (it is full rank), therefore the initial state can be found as: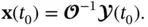
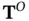 , is composed of the basis vectors of the range of
, is composed of the basis vectors of the range of 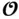 , and the unobservable subspace of the linear system, denoted by
, and the unobservable subspace of the linear system, denoted by 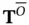 , is composed of the basis vectors of the null space of
, is composed of the basis vectors of the null space of 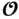 . These two subspaces can be combined to form the following nonsingular transformation matrix:
. These two subspaces can be combined to form the following nonsingular transformation matrix: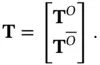
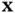 such that:
such that: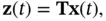
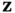 will be partitioned to observable modes,
will be partitioned to observable modes, 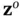 , and unobservable modes,
, and unobservable modes, 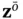 :
: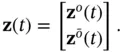
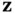 , as follows:
, as follows: