Simon Haykin - Nonlinear Filters

(2.17)

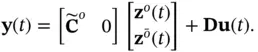
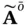Any pair of equations ( 2.14) and ( 2.15) or ( 2.16) and ( 2.17) is called the state‐space model of the system in the observable canonical form. For the system to be detectable (to have stable unobservable modes), the eigenvalues of must have negative real parts ( 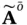must be Hurwitz ).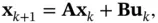

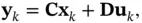
The state‐space model of a discrete‐time LTI system is represented by the following algebraic and difference equations:

(2.18)

(2.19)

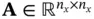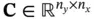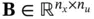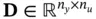where , , and are the state, the input, and the output vectors, respectively, and , , , and are the system matrices. Starting from the initial cycle, the system output vector at successive cycles up to cycle 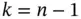can be written based on the initial state vector 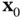and input vectors 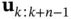as follows: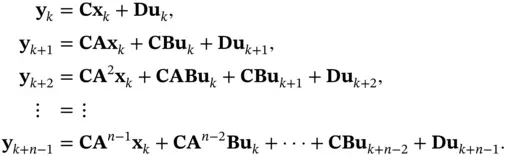

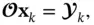
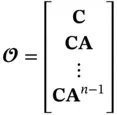
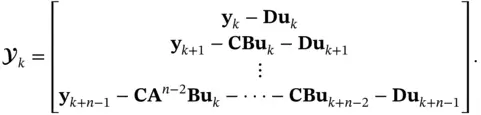
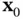(2.20)

The aforementioned equations can be rewritten in the following compact form:

(2.21)

where

(2.22)

and

(2.23)

It is obvious from the linear set of equations ( 2.21) that in order to be able to uniquely determine the initial state , matrix 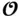must be full‐rank, provided that inputs and outputs are known. In other words, if the matrix 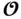is full rank, the linear system is observable or reconstructable, hence, the reason for calling 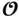the observability matrix . The reverse is true as well, if the system is observable, then the observability matrix will be full‐rank. In this case, the initial state vector can be calculated as: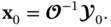

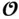(2.24)

Since depends only on matrices 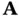and 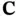, for an observable system, it is equivalently said that the pair 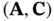is observable. Any initial state that has a component in the null space of 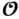cannot be uniquely determined from measurements; therefore, the null space of 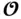is called the unobservable subspace of the system. As mentioned before, the system is detectable if the unobservable subspace does not include unstable modes of 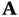, which are associated with the eigenvalues that are outside the unit circle.

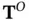While the observable subspace of the linear system, denoted by , is composed of the basis vectors of the range of 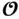, the unobservable subspace of the linear system, denoted by , is composed of the basis vectors of the null space of 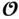. These two subspaces can be combined to form the following nonsingular transformation matrix: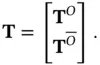

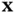(2.25)

If we apply this transformation to the state vector such that:

(2.26)