1 ...7 8 9 11 12 13 ...22 There is another difference between linear and nonlinear systems regarding observability and that is the role of inputs in nonlinear observability. While inputs do not affect the observability of a linear system, in nonlinear systems, some initial states may be distinguishable for some inputs and indistinguishable for others. This leads to the concept of uniform observability , which is the property of a class of systems, for which initial states are distinguishable for all inputs [12, 20]. Furthermore, in nonlinear systems, distinction between time‐invariant and time‐varying systems is not critical because by adding time as an extra state such as 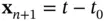 , the latter can be converted to the former [21].
, the latter can be converted to the former [21].
2.6.1 Continuous‐Time Nonlinear Systems
The state‐space model of a continuous‐time nonlinear system is represented by the following system of nonlinear equations:
(2.61) 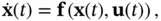
(2.62) 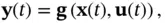
where 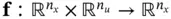 is the system function, and
is the system function, and  is the measurement function. It is common practice to deploy a control law that uses state feedback. In such cases, the control input
is the measurement function. It is common practice to deploy a control law that uses state feedback. In such cases, the control input 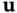 is itself a function of the state vector
is itself a function of the state vector 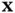 . Before proceeding, we need to recall the concept of Lie derivative from differential geometry [22, 23]. Assuming that
. Before proceeding, we need to recall the concept of Lie derivative from differential geometry [22, 23]. Assuming that 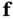 and
and 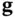 are smooth vector functions (they have derivatives of all orders or they can be differentiated infinitely many times), the Lie derivative of
are smooth vector functions (they have derivatives of all orders or they can be differentiated infinitely many times), the Lie derivative of  (the
(the 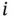 th element of
th element of 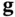 ) with respect to
) with respect to 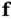 is a scalar function defined as:
is a scalar function defined as:
(2.63) 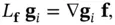
where 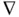 denotes the gradient with respect to
denotes the gradient with respect to 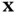 . For simplicity, arguments of the functions have not been shown. Repeated Lie derivatives are defined as:
. For simplicity, arguments of the functions have not been shown. Repeated Lie derivatives are defined as:
(2.64) 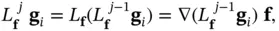
with
(2.65) 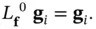
Relevance of Lie derivatives to observability of nonlinear systems becomes clear, when we consider successive derivatives of the output vector as follows:
(2.66) 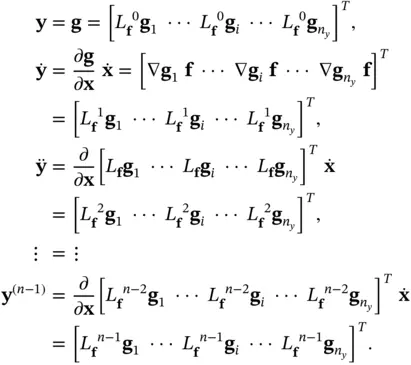
The aforementioned differential equations can be rewritten in the following compact form:
(2.67) 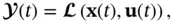
where
(2.68) 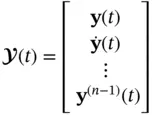
and
(2.69) 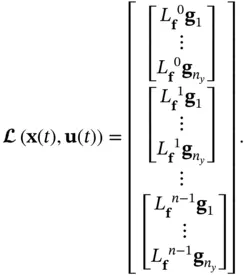
The system of nonlinear differential equations in ( 2.67) can be linearized about an initial state 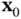 to develop a test for local observability of the nonlinear system ( 2.61) and ( 2.62) at this specific initial state, where the linearized test would be similar to the observability test for linear systems. Writing the Taylor series expansion of the function
to develop a test for local observability of the nonlinear system ( 2.61) and ( 2.62) at this specific initial state, where the linearized test would be similar to the observability test for linear systems. Writing the Taylor series expansion of the function 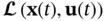 about
about 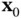 and ignoring higher‐order terms, we will have:
and ignoring higher‐order terms, we will have:
(2.70) 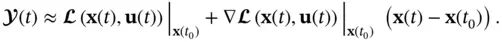
Using Cartan's formula:
(2.71) 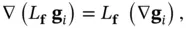
we obtain:
(2.72) 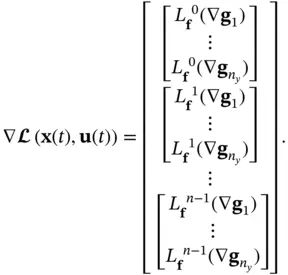
Now, we can proceed with deriving the local observability test for nonlinear systems based on the aforementioned linearized system of equations. The nonlinear system in ( 2.61) and ( 2.62) is observable at  , if there exists a neighborhood of
, if there exists a neighborhood of 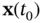 and an
and an 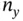 ‐tuple of integers
‐tuple of integers 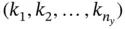 called observability indices such that [9, 24]:
called observability indices such that [9, 24]:
Читать дальше

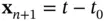 , the latter can be converted to the former [21].
, the latter can be converted to the former [21].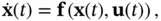
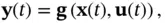
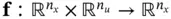 is the system function, and
is the system function, and  is the measurement function. It is common practice to deploy a control law that uses state feedback. In such cases, the control input
is the measurement function. It is common practice to deploy a control law that uses state feedback. In such cases, the control input 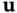 is itself a function of the state vector
is itself a function of the state vector 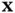 . Before proceeding, we need to recall the concept of Lie derivative from differential geometry [22, 23]. Assuming that
. Before proceeding, we need to recall the concept of Lie derivative from differential geometry [22, 23]. Assuming that 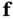 and
and 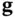 are smooth vector functions (they have derivatives of all orders or they can be differentiated infinitely many times), the Lie derivative of
are smooth vector functions (they have derivatives of all orders or they can be differentiated infinitely many times), the Lie derivative of  (the
(the 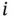 th element of
th element of 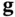 ) with respect to
) with respect to 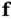 is a scalar function defined as:
is a scalar function defined as: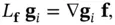
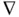 denotes the gradient with respect to
denotes the gradient with respect to 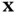 . For simplicity, arguments of the functions have not been shown. Repeated Lie derivatives are defined as:
. For simplicity, arguments of the functions have not been shown. Repeated Lie derivatives are defined as: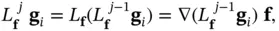
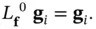
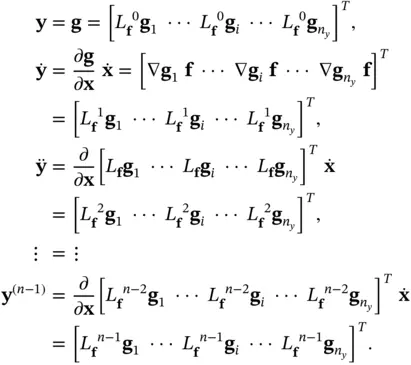
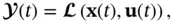
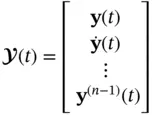

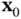 to develop a test for local observability of the nonlinear system ( 2.61) and ( 2.62) at this specific initial state, where the linearized test would be similar to the observability test for linear systems. Writing the Taylor series expansion of the function
to develop a test for local observability of the nonlinear system ( 2.61) and ( 2.62) at this specific initial state, where the linearized test would be similar to the observability test for linear systems. Writing the Taylor series expansion of the function 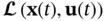 about
about 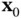 and ignoring higher‐order terms, we will have:
and ignoring higher‐order terms, we will have: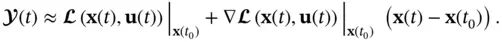
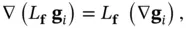
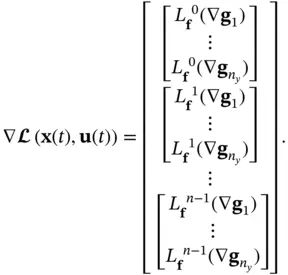
 , if there exists a neighborhood of
, if there exists a neighborhood of 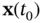 and an
and an 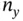 ‐tuple of integers
‐tuple of integers 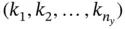 called observability indices such that [9, 24]:
called observability indices such that [9, 24]:










