Entropy can also be interpreted as the expected value of the term 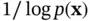 :
:
(2.97) 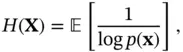
where 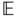 is the expectation operator and
is the expectation operator and 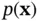 is the probability density function (PDF) of
is the probability density function (PDF) of 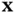 . Definition of Shannon's entropy,
. Definition of Shannon's entropy, 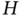 , shows that it is a function of the corresponding PDF. It will be insightful to examine the way that this information measure is affected by the shape of the PDF. A relatively broad and flat PDF, which is associated with lack of predictability, has high entropy. On the other hand, if the PDF is relatively narrow and has sharp slopes around a specific value of
, shows that it is a function of the corresponding PDF. It will be insightful to examine the way that this information measure is affected by the shape of the PDF. A relatively broad and flat PDF, which is associated with lack of predictability, has high entropy. On the other hand, if the PDF is relatively narrow and has sharp slopes around a specific value of 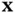 , which is associated with bias toward that particular value of
, which is associated with bias toward that particular value of 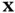 , then the PDF has low entropy. A rearrangement of the tuples
, then the PDF has low entropy. A rearrangement of the tuples 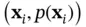 may change the shape of the PDF curve significantly but it does not affect the value of the summation or integral in ( 2.95) or ( 2.96), because summation and integration can be calculated in any order. Since
may change the shape of the PDF curve significantly but it does not affect the value of the summation or integral in ( 2.95) or ( 2.96), because summation and integration can be calculated in any order. Since 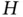 is not affected by local changes in the PDF curve, it can be considered as a global measure of the behavior of the corresponding PDF [27].
is not affected by local changes in the PDF curve, it can be considered as a global measure of the behavior of the corresponding PDF [27].
Definition 2.4 Joint entropy is defined for a pair of random vectors based on their joint distribution as:
(2.98) 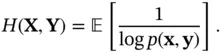
Definition 2.5 Conditional entropy is defined as the entropy of a random variable (state vector) conditional on the knowledge of another random variable (measurement vector):
(2.99) 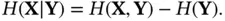
It can also be expressed as:
(2.100) 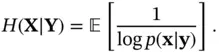
Definition 2.6 Mutual information between two random variables is a measure of the amount of information that one contains about the other. It can also be interpreted as the reduction in the uncertainty about one random variable due to knowledge about the other one. Mathematically it is defined as:
(2.101) 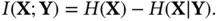
Substituting for from (2.99) into the aforementioned equation, we will have:
(2.102) 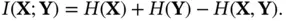
Therefore, mutual information is symmetric with respect to 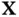 and
and  . It can also be viewed as a measure of dependence between the two random vectors. Mutual information is nonnegative; being equal to zero, if and only if
. It can also be viewed as a measure of dependence between the two random vectors. Mutual information is nonnegative; being equal to zero, if and only if 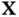 and
and 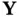 are independent. The notion of observability for stochastic systems can be defined based on the concept of mutual information.
are independent. The notion of observability for stochastic systems can be defined based on the concept of mutual information.
Definition 2.7 (Stochastic observability) The random vector (state) is unobservable from the random vector (measurement), if they are independent or equivalently . Otherwise, is observable from .
Since mutual information is nonnegative, ( 2.101) leads to the following conclusion: if either 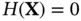 or
or 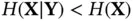 , then
, then 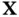 is observable from
is observable from 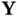 [28].
[28].
2.8 Degree of Observability
Instead of considering the notion of observability as a yes/no question, it will be helpful in practice to pose the question of how observable a system may be [29]. Knowing the answer to this question, we can select the best set of variables, which can be directly measured, as outputs to improve observability [30]. With this in mind and building on Section 2.7, mutual information can be used as a measure for the degree of observability [31].
An alternative approach aiming at providing insight into the observability of the system of interest in filtering applications uses eigenvalues of the estimation error covariance matrix. The largest eigenvalue of the covariance matrix is the variance of the state or a function of states, which is poorly observable. Hence, its corresponding eigenvector provides the direction of poor observability. On the other hand, states or functions of states that are highly observable are associated with smaller eigenvalues, where their corresponding eigenvectors provide the directions of good observability [30].
A deterministic system is either observable or unobservable, but for stochastic systems, the degree of observability can be defined as [32]:
(2.103) 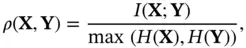
which is a time‐dependent non‐decreasing function that varies between 0 and 1. Before starting the measurement process, 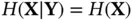 and therefore,
and therefore, 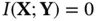 , which makes
, which makes 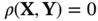 . As more measurements become available,
. As more measurements become available, 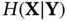 may reduce and therefore,
may reduce and therefore, 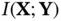 may increase, which leads to the growth of
may increase, which leads to the growth of 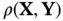 up to 1 [33].
up to 1 [33].
Читать дальше

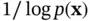 :
: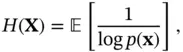
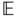 is the expectation operator and
is the expectation operator and 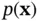 is the probability density function (PDF) of
is the probability density function (PDF) of 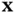 . Definition of Shannon's entropy,
. Definition of Shannon's entropy, 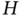 , shows that it is a function of the corresponding PDF. It will be insightful to examine the way that this information measure is affected by the shape of the PDF. A relatively broad and flat PDF, which is associated with lack of predictability, has high entropy. On the other hand, if the PDF is relatively narrow and has sharp slopes around a specific value of
, shows that it is a function of the corresponding PDF. It will be insightful to examine the way that this information measure is affected by the shape of the PDF. A relatively broad and flat PDF, which is associated with lack of predictability, has high entropy. On the other hand, if the PDF is relatively narrow and has sharp slopes around a specific value of 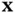 , which is associated with bias toward that particular value of
, which is associated with bias toward that particular value of 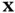 , then the PDF has low entropy. A rearrangement of the tuples
, then the PDF has low entropy. A rearrangement of the tuples 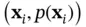 may change the shape of the PDF curve significantly but it does not affect the value of the summation or integral in ( 2.95) or ( 2.96), because summation and integration can be calculated in any order. Since
may change the shape of the PDF curve significantly but it does not affect the value of the summation or integral in ( 2.95) or ( 2.96), because summation and integration can be calculated in any order. Since 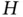 is not affected by local changes in the PDF curve, it can be considered as a global measure of the behavior of the corresponding PDF [27].
is not affected by local changes in the PDF curve, it can be considered as a global measure of the behavior of the corresponding PDF [27].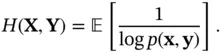
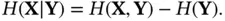
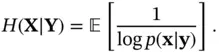
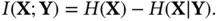
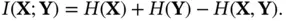
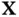 and
and  . It can also be viewed as a measure of dependence between the two random vectors. Mutual information is nonnegative; being equal to zero, if and only if
. It can also be viewed as a measure of dependence between the two random vectors. Mutual information is nonnegative; being equal to zero, if and only if 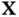 and
and 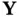 are independent. The notion of observability for stochastic systems can be defined based on the concept of mutual information.
are independent. The notion of observability for stochastic systems can be defined based on the concept of mutual information.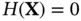 or
or 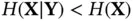 , then
, then 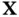 is observable from
is observable from 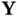 [28].
[28].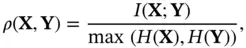
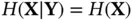 and therefore,
and therefore, 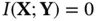 , which makes
, which makes 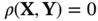 . As more measurements become available,
. As more measurements become available, 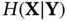 may reduce and therefore,
may reduce and therefore, 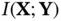 may increase, which leads to the growth of
may increase, which leads to the growth of 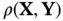 up to 1 [33].
up to 1 [33].










