Jacques Simon - Continuous Functions

1 Cover

2 Title Page Analysis for PDEs Set coordinated by Jacques Blum

3 Copyright Page First published 2020 in Great Britain and the United States by ISTE Ltd and John Wiley & Sons, Inc. Apart from any fair dealing for the purposes of research or private study, or criticism or review, as permitted under the Copyright, Designs and Patents Act 1988, this publication may only be reproduced, stored or transmitted, in any form or by any means, with the prior permission in writing of the publishers, or in the case of reprographic reproduction in accordance with the terms and licenses issued by the CLA. Enquiries concerning reproduction outside these terms should be sent to the publishers at the undermentioned address: ISTE Ltd 27-37 St George’s Road London SW19 4EU UK www.iste.co.uk John Wiley & Sons, Inc. 111 River Street Hoboken, NJ 07030 USA www.wiley.com © ISTE Ltd 2020 The rights of Jacques Simon to be identified as the author of this work have been asserted by him in accordance with the Copyright, Designs and Patents Act 1988. Library of Congress Control Number: 2020933955 British Library Cataloguing-in-Publication Data A CIP record for this book is available from the British Library ISBN 978-1-78630-010-2

4 Introduction

5 Familiarization with Semi-normed Spaces

6 Notations

7 Chapter 1: Spaces of Continuous Functions 1.1 Notions of continuity 1.2 Spaces С(Ω; E), С b(Ω; E), С K(Ω; E), С(Ω; E) and С b(Ω; E) 1.3 Comparison of spaces of continuous functions 1.4 Sequential completeness of spaces of continuous functions 1.5 Metrizability of spaces of continuous functions 1.6 The space 1.7 Continuous mappings 1.8 Continuous extension and restriction 1.9 Separation and permutation of variables 1.10 Sequential compactness in C b(Ω; E)

8 Chapter 2: Differentiable Functions 2.1 Differentiability 2.2 Finite increment theorem 2.3 Partial derivatives 2.4 Higher order partial derivatives 2.5 Spaces and 2.6 Comparison and metrizability of spaces of differentiable functions 2.7. Filtering properties of spaces of differentiable functions 2.8. Sequential completeness of spaces of differentiable functions 2.9. The space and the set

9 Chapter 3: Differentiating Composite Functions and Others 3.1. Image under a linear mapping 3.2. Image under a multilinear mapping: Leibniz rule 3.3. Dual formula of the Leibniz rule 3.4. Continuity of the image under a multilinear mapping 3.5. Change of variables in a derivative 3.6. Differentiation with respect to a separated variable 3.7. Image under a differentiable mapping 3.8. Differentiation and translation 3.9. Localizing functions

10 Chapter 4: Integrating Uniformly Continuous Functions 4.1. Measure of an open subset of 4.2. Integral of a uniformly continuous function 4.3. Case where Eis not a Neumann space 4.4. Properties of the integral 4.5. Dependence of the integral on the domain of integration 4.6. Additivity with respect to the domain of integration 4.7. Continuity of the integral 4.8. Differentiating under the integral sign

11 Chapter 5: Properties of the Measure of an Open Set 5.1. Additivity of the measure 5.2. Negligible sets 5.3. Determinant of dvectors 5.4. Measure of a parallelepiped

12 Chapter 6: Additional Properties of the Integral 6.1. Contribution of a negligible set to the integral 6.2. Integration and differentiation in one dimension 6.3. Integration of a function of functions 6.4. Integrating a function of multiple variables 6.5. Integration between graphs 6.6. Integration by parts and weak vanishing condition for a function 6.7. Change of variables in an integral 6.8. Some particular changes of variables in an integral

13 Chapter 7: Weighting and Regularization of Functions 7.1. Weighting 7.2. Properties of weighting 7.3. Weighting of differentiable functions 7.4. Local regularization 7.5. Global regularization 7.6. Partition of unity 7.7. Separability of K ∞(Ω)

14 Chapter 8: Line Integral of a Vector Field Along a Path 8.1. Paths 8.2. Line integral of a field along a path 8.3. Line integral along a concatenation of paths 8.4. Tubular flow and the concentration theorem 8.5. Invariance under homotopy of the line integral of a local gradient

15 Chapter 9: Primitives of Continuous Functions 9.1. Explicit primitive of a field with line integral zero 9.2. Primitive of a field orthogonal to the divergence-free test fields 9.3. Gluing of local primitives on a simply connected open set 9.4. Explicit primitive on a star-shaped set: Poincaré’s theorem 9.5. Explicit primitive under the weak Poincaré condition 9.6. Primitives on a simply connected open set 9.7. Comparison of the existence conditions for a primitive 9.8. Fields with local primitives but no global primitive 9.9. Uniqueness of primitives 9.10. Continuous primitive mapping

16 Chapter 10: Additional Results: Integration on a Sphere 10.1. Surface integration on a sphere 10.2. Properties of the integral on a sphere 10.3. Radial calculation of integrals 10.4. Surface integral as an integral of dimension d− 1 10.5. A Stokes formula

17 Appendix: Reminders A.1. Notation and numbering A.2. Semi-normed spaces A.3. Continuous mappings and duality A.4. Differentiable mappings and differentiable functions

18 Bibliography

19 Index

20 Other titles from ISTE in Mathematics and Statistics

21 End User License Agreement

1 Chapter 4Figure 4.1 Paving ω by the cubes Δ s,n

2 Chapter 5Figure 5.1 Equivalent decompositions for “measuring” a parallelepiped ...

3 Chapter 6Figure 6.1. Domain delimited by the graphs of ϒ 1 and ϒ 2Figure 6.2. Change of variables.

4 Chapter 7Figure 7.1 Domain Ω D of the weighted function f ⋄ μ Figure 7.2 Domain Ω K extending up to part of the boundary. The contour of Ω KFigure 7.3 Crown-shaped set κn and potato-shaped set ....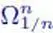

5 Chapter 8Figure 8.1 Divergence-free tubular flow in the tube T of axis [Γ]Figure 8.2 Intermediate closed paths

6 Chapter 9Figure 9.1 Subset that is star shaped with respect to a . 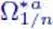is dark gray an ...Figure 9.2 Field q with local primitive θ but no global primitive. The set ...

7 Chapter 10Figure 10.1 Decomposition of the crown C r,r+ϵ. A is dark gray and L i ...

1 Cover

2 Table of Contents

3 Begin Reading

1 ii To Claire and Patricia, By your gaiety, “joie de vivre”, and femininity, you have embellished my life, and you have allowed me to conserve the tenacity needed for this endeavor