Jacques Simon - Continuous Functions

Moreover, sequential completeness is more straightforward than completeness.

Semi-norms.We use families of semi-norms, instead of the equivalent notion of locally convex topologies, to be able to define differentiability (p. 73) by comparing the semi-norms of a variation of the variable to the semi-norms of the variation of the value. A section on Familiarization with Semi-normed Spaces can be found on p. xiii. Semi-norms can be manipulated in a similar fashion to normed spaces, except that we are working with several semi-norms instead of a single norm.

Primitives.We show that any continuous field q = ( q 1, . . . , q d) on an open set Ω of ℝ dhas a primitive f , namely that ∇ f = q , if and only if it is orthogonal to the divergence-free test fields, that is, if 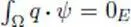for every ψ = ( ψ 1, . . . , ψ d) such that ∇ · ψ = 0. This is the orthogonality theorem (Theorem 9.2).

When Ω is simply connected, for a primitive f to exist, it is necessary and sufficient for q to have local primitives. This is the local primitive gluing theorem (Theorem 9.4). On any such open set, it is also necessary and sufficient that it verifies Poincaré’s condition ∂ i q i= ∂ j q ifor every i and j to be satisfied if the field is C 1(Theorem 9.10), or a weak version of this condition, 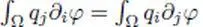for every test function φ , if the field is continuous (Theorem 9.11).

We explicitly determine all primitives (Theorem 9.17) and construct one that depends continuously on q (Theorem 9.18).

Integration.We extend the Cauchy integral to uniformly continuous functions taking values in a Neumann space, because this will be an essential tool for constructing primitives.

The properties established here for continuous functions will also be used to extend them to integrable distributions in Volume 4, by continuity or transposition. Indeed, one of the objectives of the Analysis for PDEs series is to extend integration and Sobolev spaces to take values in Neumann spaces. However, it seemed more straightforward to first construct distributions (in Volume 3) using just continuous functions before introducing integrable distributions (in Volume 4), which play the role usually fulfilled by classes of almost everywhere equal integrable functions.

Weighting.The weighted function of a function f defined on an open set Ω by the weight μ, a real function with compact support D , is a function defined on the open set 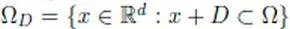by 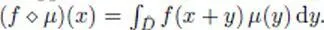This concept will be repeatedly useful. It plays an analogous role to convolution, which is equivalent to it up to a symmetry of μ when .

Novelties.Many results are natural extensions of previous results, but the following seemed most noteworthy:

— The construction of the topology of the space 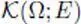of continuous functions with compact support using the semi-norms 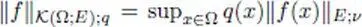indexed by 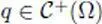and 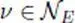( Definition 1.17). This is equivalent to and much simpler than the inductive limit topology of the .

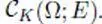— The fact that if a function 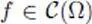satisfies 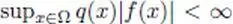for every 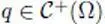, then its support is compact ( Theorem 1.22). This is the basis for defining the semi-norms of 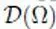in Volume 3.

— The concentration theorem for the integral and the construction of an incompressible tubular flow (Theorems 8.18 and 8.17), which are key steps in our construction of the primitives of a field taking values in a Neumann space, as it is explained in the comment Utility of the concentration theorem, p. 186.

Prerequisites.The proofs in the main body of the text only use definitions and results established in Volume 1, whose statements are recalled either in the text or in the Appendix. Detailed proofs are given, including arguments that may seem trivial to experienced readers, and the theorem numbers are systematically referenced.

Comments.Comments with a smaller font size than the main body of the text appeal to external results or results that have not yet been established. The Appendix on Reminders is also written with a smaller font size, since its contents are assumed to be familiar.

Historical notes.Wherever possible, the origin of the concepts and results is given as a footnote 2.

Navigation through the book:

— The Table of Contentsat the start of the book lists the topics discussed.

— The Table of Notations, p. xv, specifies the meaning of the notation in case there is any doubt.

— The Index, p. 243, provides an alternative access to specific topics.

— All hypotheses are stated directly within the theorems themselves.

— The numbering scheme is shared across every type of statement to make results easier to find by number (for instance, Theorem 2.9 is found between the statements 2.8 and 2.10, which are a definition and a theorem, respectively).

Acknowledgments.Enrique FERNÁNDEZ-CARA suggested to me a large number of improvements to various versions of this work. Jérôme LEMOINE was kind enough to proofread the countless versions of the book and correct just as many mistakes and oversights.