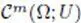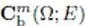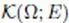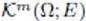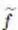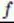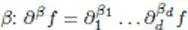— A Fréchetspace is a sequentially complete metrizable semi-normed space.
— A Banachspace is a sequentially complete normed space.
Advantages of using semi-norms rather than topology:
— Semi-norms allow the definition of Lp (Ω; E ) (by raising the semi-norms of E to the power p ).
— They allow the definition of the differentiability of a mapping from a semi-normed space into another (by comparing the semi-norms of an increase in the variable to the semi-norms of the increase in the value).
— They are easy to manipulate: working with them is just like working with normed spaces, the main difference being that there are several semi-norms or norms instead of a single norm.
— Some definitions are simpler, for example that of a bounded set  for any semi-norm || || E;v of E ” would be expressed, in terms of topology, in the more abstract form “for any open set V containing 0 E, there is t > 0 such that tU ⊂ V ”.
for any semi-norm || || E;v of E ” would be expressed, in terms of topology, in the more abstract form “for any open set V containing 0 E, there is t > 0 such that tU ⊂ V ”.
Notations
SPACES OF FUNCTIONS
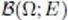 |
space of uniformly continuous functions with bounded support |
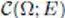 |
space of continuous functions |
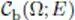 |
space of bounded continuous functions |
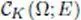 |
space of continuous functions with support included in the compact set K ⊂ Ω |
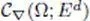 |
space of gradients of continuous functions |
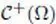 |
set of positive continuous real functions |
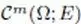 |
space of m times continuously differentiable functions, and the case m = ∞ |
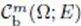 |
id. with bounded derivatives, and the case m = ∞ |
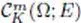 |
id. with support included in the compact set K ⊂ Ω, and the case m = ∞ |
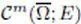 |
space  defined on the closure of a bounded open set defined on the closure of a bounded open set |
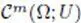 |
set of functions in  taking values in the set U taking values in the set U |
| C(Ω; E ) |
space of uniformly continuous functions |
| C b(Ω; E ) |
space of bounded uniformly continuous functions |
| C D(Ω; E ) |
id. with support included in the compact subset D of ℝ d |
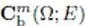 |
space  with uniformly continuous bounded derivatives, and the case m = ∞ with uniformly continuous bounded derivatives, and the case m = ∞ |
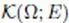 |
space of continuous functions with compact support |
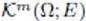 |
id. m times continuously differentiable, and the case m = ∞ |
OPERATIONS ON A FUNCTION f
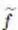 |
extension by 0 E |
 |
image under permutation of variables |
 |
image under the symmetry x ↦ − x of the variable |
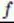 |
image under separation of variables |
| τxf |
translation by x ∈ ℝ d |
| Rnf |
global regularization |
| f ⋄ μ |
function weighted by μ |
| f ⋄ ρn |
local regularization |
| f * μ |
convolution with μ |
| f ⨂ g |
tensor product with g |
| f ∘ T |
composition with T |
| supp f |
support |
| Lf or L ∘ f |
composition with the linear mapping L |
DERIVATIVES OF A FUNCTION f
| f ʹ or d f /d x |
derivative of a function of a single real variable |
| ∂if |
partial derivative: ∂if = ∂f/∂xi |
| ∂β f |
derivative of order 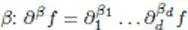 |
| β |
positive multi-integer: β = ( β 1,…, βd ), βi ≥ 0 |
| |β| |
differentiability order: | β | = | β 11 + … | βd | |
| ∂0f |
derivative of order 0: ∂0 f = f |
| ∇ f |
gradient: ∇ f = ( ∂1f ,…, ∂df ) |
| d f |
differential |
| q |
field: q = ( q1 ,…, qd ) |
| ∇· q |
divergence: ∇ · q = ∂ 1 q 1+ … ∂dqd |
| ∇ −1 q |
primitive that depends continuously on q |
| q* |
explicit primitive: q *( x ) = f Γ(a, x) q · dℓ |
Читать дальше

 for any semi-norm || || E;v of E ” would be expressed, in terms of topology, in the more abstract form “for any open set V containing 0 E, there is t > 0 such that tU ⊂ V ”.
for any semi-norm || || E;v of E ” would be expressed, in terms of topology, in the more abstract form “for any open set V containing 0 E, there is t > 0 such that tU ⊂ V ”.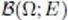
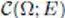
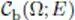
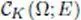
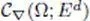
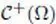
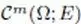
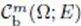
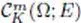
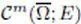
 defined on the closure of a bounded open set
defined on the closure of a bounded open set