Olivier BESSON, Fulbert MIGNOT, Nicolas DEPAUW, and Didier BRESCH also provided many improvements, in form and in substance.
Pierre DREYFUSS gave me insight into the necessity of simply connected domains for the existence of primitives with Poincaré’s condition, as explained on p. 209 in the comment Is simple connectedness necessary for gluing together local primitives?
Joshua PEPPER spent much time discussing about the best way to adapt this work in English.
Thank you, my friends.
Jacques SIMON
Chapdes-Beaufort
April 2020
1 1 Students? What might I have answered if one of my MAS students in 1988 had asked for more details about the de Rham duality theorem that I used to obtain the pressure in the Navier-Stokes equations? Perhaps I could say that “Jacques-Louis LIONS, my supervisor, wrote that it follows from the de Rham cohomology theorem, of which I understand neither the statement, nor the proof, nor why it implies the result that we are using.” What a despicably unscientific appeal to authority!This question was the starting point of this work: writing proofs that I can explain to my students for every result that I use. It took me 5 years to find the “elementary” proof of the orthogonality theorem (Theorem 9.2, p. 194) on the existence of the primitives of a field q. I needed a way to obtain fr q • Ai = 0 for every closed path r from the condition fn q • y = 0 for every divergence-free y. It gave me the greatest mathematical satisfaction I have ever experienced to explicitly construct an incompressible tubular flow (see p. 184). Twenty-five years later, I am finally ready to answer any other questions from my (very persistent) students.
2 2 Appeal to the reader. Many important results lack historical notes because I am not familiar with their origins. I hope that my readers will forgive me for these omissions and any injustices they may discover. And I encourage the scholars among you to notify me of any improvements for future editions!
Familiarization with Semi-normed Spaces
A semi-normed space E is a vector space endowed with a family 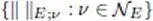 of semi-norms.
of semi-norms.
— The set NE indexing the semi-norms is, a priori , arbitrary.
— A normedspace is the special case where this family simply consists of a single norm.
— Every locally convex topological vector space can be endowed with a family of semi-norms that generates its topology (Neumann’s theorem).
— We only consider separated spaces, namely in which || u || E;v= 0 for every v ∈ NE , then u = 0 E .
Working with semi-normed spaces:
— un → u in E means that || un − u || E;v→ 0 for every v ∈ NE .
— U is bounded in E means that 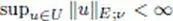 for every v ∈ NE .
for every v ∈ NE .
— T is continuousfrom F into E at the point u means that, for every v ∈ NE and ϵ > 0, there exists a finite set M of NF and η > 0 such that 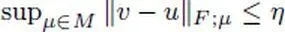 implies
implies 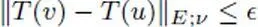 .
.
Examples — real-valued function spaces:
— The space C b(Ω) of continuous and bounded functions is endowed with the norm 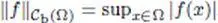
— C (Ω) is endowed with the semi-norms 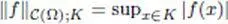 indexed by the compact sets K ⊂ Ω.
indexed by the compact sets K ⊂ Ω.
— Lp (Ω) is endowed with the norm 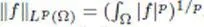 .
.
— 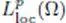 is endowed with the semi-norms
is endowed with the semi-norms 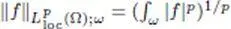 indexed by the bounded open sets ω such that ϖ ⊂ Ω.
indexed by the bounded open sets ω such that ϖ ⊂ Ω.
Examples — abstract-valued function spaces:
— C b(Ω; E ) is endowed with the semi-norms 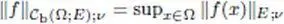 indexed by v ∈ NE
indexed by v ∈ NE
— C (Ω; E ) is endowed with the semi-norms 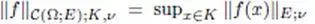 indexed by the compact sets K ⊂ Ω and v ∈ NE
indexed by the compact sets K ⊂ Ω and v ∈ NE
— L p(Ω; E ) is endowed with the semi-norms 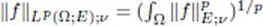 indexed by v ∈ NE .
indexed by v ∈ NE .
Examples — weak space, dual space:
— E -weak is endowed with the semi-norms 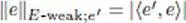 indexed by e′ ∈ E′ .
indexed by e′ ∈ E′ .
— E′ is endowed with the semi-norms 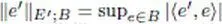 indexed by the bounded sets B of E .
indexed by the bounded sets B of E .
— E′ -weak is endowed with the semi-norms 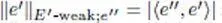 indexed by e″ ∈ E″ .
indexed by e″ ∈ E″ .
— E′ - *weak is endowed with the semi-norms 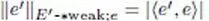 indexed by e ∈ E .
indexed by e ∈ E .
Neumann spaces and others:
— A sequentially completespace is a space in which every Cauchy sequence converges.
— A Neumannspace is a sequentially complete separated semi-normed space.
Читать дальше

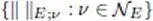 of semi-norms.
of semi-norms.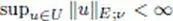 for every v ∈ NE .
for every v ∈ NE .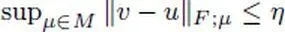 implies
implies 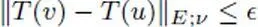 .
.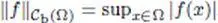
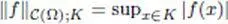 indexed by the compact sets K ⊂ Ω.
indexed by the compact sets K ⊂ Ω.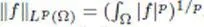 .
. is endowed with the semi-norms
is endowed with the semi-norms 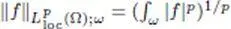 indexed by the bounded open sets ω such that ϖ ⊂ Ω.
indexed by the bounded open sets ω such that ϖ ⊂ Ω.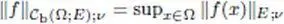 indexed by v ∈ NE
indexed by v ∈ NE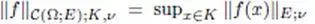 indexed by the compact sets K ⊂ Ω and v ∈ NE
indexed by the compact sets K ⊂ Ω and v ∈ NE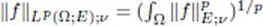 indexed by v ∈ NE .
indexed by v ∈ NE .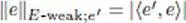 indexed by e′ ∈ E′ .
indexed by e′ ∈ E′ .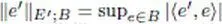 indexed by the bounded sets B of E .
indexed by the bounded sets B of E .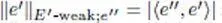 indexed by e″ ∈ E″ .
indexed by e″ ∈ E″ .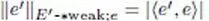 indexed by e ∈ E .
indexed by e ∈ E .










