A deterministic discrete‐time linear system is described by the following state‐space model:
(3.1) 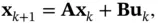
(3.2) 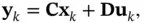
where  ,
, 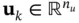 , and
, and  denote state, input, and output vectors, respectively, and
denote state, input, and output vectors, respectively, and 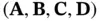 are the model parameters, which are matrices with appropriate dimensions. Luenberger observer is a sequential or recursive state estimator, which needs the information of only the previous sample time to reconstruct the state as:
are the model parameters, which are matrices with appropriate dimensions. Luenberger observer is a sequential or recursive state estimator, which needs the information of only the previous sample time to reconstruct the state as:
(3.3) 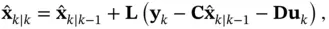
where 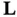 is a constant gain matrix, which is determined in a way that the closed‐loop system achieves some desired performance criteria. The predicted estimate,
is a constant gain matrix, which is determined in a way that the closed‐loop system achieves some desired performance criteria. The predicted estimate, 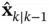 , is obtained from ( 3.1) as:
, is obtained from ( 3.1) as:
(3.4) 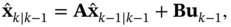
with the initial condition 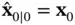 .
.
The dynamic response of the state reconstruction error, 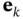 , from an initial nonzero value is governed by:
, from an initial nonzero value is governed by:
(3.5) 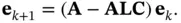
The gain matrix, 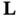 , is determined by choosing the closed‐loop observer poles, which are the eigenvalues of
, is determined by choosing the closed‐loop observer poles, which are the eigenvalues of 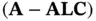 . Using the pole placement method to design the Luenberger observer requires the system observability. In order to have a stable observer, moduli of the eigenvalues of
. Using the pole placement method to design the Luenberger observer requires the system observability. In order to have a stable observer, moduli of the eigenvalues of 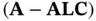 must be strictly less than one. A deadbeat observer is obtained, if all the eigenvalues are zero. The Luenberger observer is designed based on a compromise between rapid decay of the reconstruction error and sensitivity to modeling error and measurement noise [9]. Section 3.3provides an extension of the Luenberger observer for nonlinear systems.
must be strictly less than one. A deadbeat observer is obtained, if all the eigenvalues are zero. The Luenberger observer is designed based on a compromise between rapid decay of the reconstruction error and sensitivity to modeling error and measurement noise [9]. Section 3.3provides an extension of the Luenberger observer for nonlinear systems.
3.3 Extended Luenberger‐Type Observer
A class of nonlinear observers is designed based on observer error linearization. State estimation by such observers involves multiplication of a matrix gain by the difference between predicted and measured outputs. After designing the observer (selecting the observer gain), this calculation can be performed fairly quickly, which is an advantage from the computational complexity perspective. However, the domain of applicability of such observers may be restricted to a specific class of nonlinear systems. A discrete‐time nonlinear Luenberger‐type observer has been proposed in [36]. A deterministic discrete‐time nonlinear system is described by the following state‐space model:
(3.6) 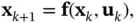
(3.7) 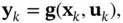
where 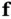 and
and 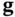 are nonlinear vector functions. At time instant
are nonlinear vector functions. At time instant  , let
, let 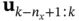 denote the sequence of the past
denote the sequence of the past 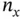 inputs:
inputs:
(3.8) 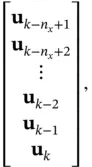
where 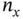 is the dimension of the state vector. Given an initial state and a sequence of previous inputs, a series of predicted outputs can be generated using the state equation ( 3.6) as:
is the dimension of the state vector. Given an initial state and a sequence of previous inputs, a series of predicted outputs can be generated using the state equation ( 3.6) as:
(3.9) 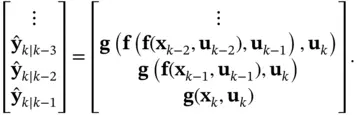
Let  denote the
denote the 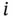 th composite of the system function
th composite of the system function 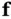 as:
as:
(3.10) 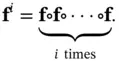
Given an initial state and the sequence 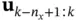 , the corresponding sequence of predicted outputs is obtained as:
, the corresponding sequence of predicted outputs is obtained as:
(3.11) 
Читать дальше

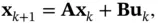
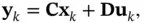
 ,
, 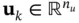 , and
, and  denote state, input, and output vectors, respectively, and
denote state, input, and output vectors, respectively, and 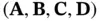 are the model parameters, which are matrices with appropriate dimensions. Luenberger observer is a sequential or recursive state estimator, which needs the information of only the previous sample time to reconstruct the state as:
are the model parameters, which are matrices with appropriate dimensions. Luenberger observer is a sequential or recursive state estimator, which needs the information of only the previous sample time to reconstruct the state as: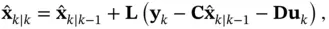
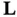 is a constant gain matrix, which is determined in a way that the closed‐loop system achieves some desired performance criteria. The predicted estimate,
is a constant gain matrix, which is determined in a way that the closed‐loop system achieves some desired performance criteria. The predicted estimate, 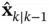 , is obtained from ( 3.1) as:
, is obtained from ( 3.1) as: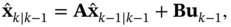
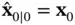 .
.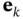 , from an initial nonzero value is governed by:
, from an initial nonzero value is governed by: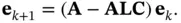
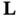 , is determined by choosing the closed‐loop observer poles, which are the eigenvalues of
, is determined by choosing the closed‐loop observer poles, which are the eigenvalues of 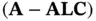 . Using the pole placement method to design the Luenberger observer requires the system observability. In order to have a stable observer, moduli of the eigenvalues of
. Using the pole placement method to design the Luenberger observer requires the system observability. In order to have a stable observer, moduli of the eigenvalues of 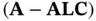 must be strictly less than one. A deadbeat observer is obtained, if all the eigenvalues are zero. The Luenberger observer is designed based on a compromise between rapid decay of the reconstruction error and sensitivity to modeling error and measurement noise [9]. Section 3.3provides an extension of the Luenberger observer for nonlinear systems.
must be strictly less than one. A deadbeat observer is obtained, if all the eigenvalues are zero. The Luenberger observer is designed based on a compromise between rapid decay of the reconstruction error and sensitivity to modeling error and measurement noise [9]. Section 3.3provides an extension of the Luenberger observer for nonlinear systems.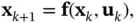
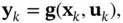
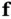 and
and 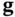 are nonlinear vector functions. At time instant
are nonlinear vector functions. At time instant  , let
, let 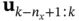 denote the sequence of the past
denote the sequence of the past 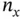 inputs:
inputs: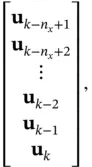
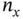 is the dimension of the state vector. Given an initial state and a sequence of previous inputs, a series of predicted outputs can be generated using the state equation ( 3.6) as:
is the dimension of the state vector. Given an initial state and a sequence of previous inputs, a series of predicted outputs can be generated using the state equation ( 3.6) as: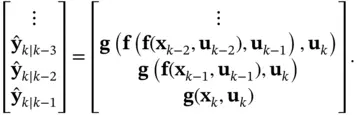
 denote the
denote the 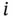 th composite of the system function
th composite of the system function 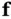 as:
as: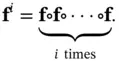
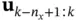 , the corresponding sequence of predicted outputs is obtained as:
, the corresponding sequence of predicted outputs is obtained as:











