Observability can be studied regarding the characteristics of the information set, 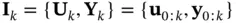 as well as the invertibility property of the corresponding maps. From this viewpoint, information sets can be divided into three categories [34]:
as well as the invertibility property of the corresponding maps. From this viewpoint, information sets can be divided into three categories [34]:
Instantaneously invertible: In this case, full information can be recovered and it would not be necessary to use a filter.
Asymptotically invertible: A filter can provide a solution that converges to the true values of states. In this case, the deployed filter may recover information with fewer observables compared with the instantaneously invertible case.
Noninvertible: In this case, even a filter cannot replicate full information.
For systems with unknown inputs , a subset of the inputs to the system may be unknown. For such systems, assuming that the initial state is known, it is often desired to reconstruct the unknown inputs through dynamic system inversion . Since a number of faults and attacks can be modeled as unknown inputs to the system, the concept of invertibility is important in fault diagnosis and cybersecurity. To be more precise, the following definitions are recalled from [35].
Definition 2.8 (‐delay inverse) The system described by the state‐space model (2.18) and (2.19) has an ‐delay inverse, if its input at time step , , can be uniquely recovered from the outputs up to time step , , for some nonnegative integer , assuming that the initial state is known.
Definition 2.9 (Invertibility) The system with the state‐space model (2.18) and (2.19) is invertible, if it has an ‐delay inverse for some finite , where the inherent delay of the system is the least integer for which an ‐delay inverse exists.
The topic of invertibility will be further discussed in Section 3.5, which covers the unknown input observers .
Observability is a key property of dynamic systems, which deals with the question of whether the state of a system can be uniquely determined in a finite time interval from inputs and measured outputs provided that the system dynamic model is known:
For linear systems, observability is a global property and there is a universal definition for it. An LTI (LTV) system is observable, if and only if its observability matrix (observability Gramian matrix) is full‐rank, and the state can be reconstructed from inputs and measured outputs using the inverse of the observability matrix (observability Gramian matrix).
For nonlinear systems, a unique definition of observability does not exist and locally weak observability is considered in a neighborhood of the initial state. A nonlinear system is locally weakly observable if its Jacobian matrix about that particular state has full rank. Then, the initial state can be reconstructed from inputs and measured outputs using the inverse of the Jacobian.
For stochastic systems, mutual information between states and outputs can be used as a measure for the degree of observability, which helps to reconfigure the sensory (perceptual) part of the system in a way to improve the observability [33].
3 Observers
3.1 Introduction
State of a system refers to the minimum amount of information, which is required at the current time instant to uniquely describe the dynamic behavior of the system in the future, given the inputs and parameters. Parameters reflect the physical properties used in a model as a description of the system under study. Inputs or actions are manipulated variables that act on the dynamic system as forcing functions. Outputs or observations are variables that can be directly measured. In many practical situations, the full state of a dynamic system cannot be directly measured. Hence, the current state of the system must be reconstructed from the known inputs and the measured outputs. State estimation is deployed as a process to determine the state from inputs and outputs given a dynamic model of the system. For linear systems, reconstruction of system state can be performed by deploying the well‐established optimal linear estimation theory. However, for nonlinear systems, we need to settle for sub‐optimal methods, which are computationally tractable and can be implemented in real‐time applications. Such methods rely on simplifications of or approximations to the underlying nonlinear system in the presence of uncertainty [9]. In this chapter, starting from deterministic linear state estimation, the stage will be set for nonlinear methods, and then, unknown inputs such as faults and attacks will be discussed. Since state estimators are usually implemented using digital processors, emphasis will be put on methods in which measurements are available at discrete sampling times. There are two classes of observers regarding the order of the observer as a dynamic system and the order of the system under study whose state is to be estimated:
Full‐order observers: The order of the observer is equal to the order of the main system.
Reduced‐order observers: The order of the observer is less than the order of the main system.
In the following, the symbol “ 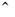 ” denotes the estimated variable. Since such variable is determined based on the measured outputs, for clarification, two time indices will be used: one for the estimate and the other for the measurement. For discrete‐time systems,
” denotes the estimated variable. Since such variable is determined based on the measured outputs, for clarification, two time indices will be used: one for the estimate and the other for the measurement. For discrete‐time systems, 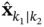 denotes the estimate of the state,
denotes the estimate of the state, 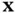 , at time instant
, at time instant 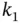 , given output measurements up to time instant
, given output measurements up to time instant 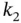 . Similarly, for continuous‐time systems,
. Similarly, for continuous‐time systems, 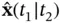 denotes the estimate of the state,
denotes the estimate of the state, 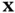 , at time instant
, at time instant 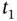 , given output measurements up to time instant
, given output measurements up to time instant 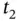 . The estimate
. The estimate 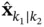 is
is
a smoothed state estimate, if ,
a filtered state estimate, if , and
a predicted state estimate, if .
For control applications, usually the control law uses the filtered state estimate, which is the current estimate based on all available measurements. The predicted estimate relies on the state transition model to extrapolate the filtered estimate into the future. Such estimates are usually used for computing the objective or cost function in model predictive control. Smoothed estimates are computed in an offline manner based on both past and future measurements. They provide a more accurate estimate than the filtered ones. They are usually used for process analysis and diagnosis [9].
Читать дальше

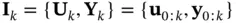 as well as the invertibility property of the corresponding maps. From this viewpoint, information sets can be divided into three categories [34]:
as well as the invertibility property of the corresponding maps. From this viewpoint, information sets can be divided into three categories [34]: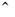 ” denotes the estimated variable. Since such variable is determined based on the measured outputs, for clarification, two time indices will be used: one for the estimate and the other for the measurement. For discrete‐time systems,
” denotes the estimated variable. Since such variable is determined based on the measured outputs, for clarification, two time indices will be used: one for the estimate and the other for the measurement. For discrete‐time systems, 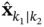 denotes the estimate of the state,
denotes the estimate of the state, 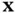 , at time instant
, at time instant 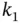 , given output measurements up to time instant
, given output measurements up to time instant 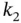 . Similarly, for continuous‐time systems,
. Similarly, for continuous‐time systems, 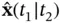 denotes the estimate of the state,
denotes the estimate of the state, 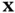 , at time instant
, at time instant 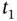 , given output measurements up to time instant
, given output measurements up to time instant 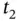 . The estimate
. The estimate 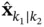 is
is










