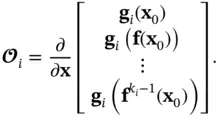1 ...8 9 10 12 13 14 ...22 1 for .
2 The row vectors of are linearly independent.
From the row vectors 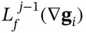 , an observability matrix can be constructed for the continuous‐time nonlinear system in ( 2.61) and ( 2.62) as follows:
, an observability matrix can be constructed for the continuous‐time nonlinear system in ( 2.61) and ( 2.62) as follows:
(2.73) 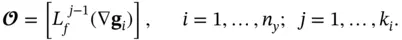
If 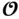 is full‐rank, then the nonlinear system in ( 2.61) and ( 2.62) is locally weakly observable. It is worth noting that the observability matrix for continuous‐time linear systems ( 2.7) is a special case of the observability matrix for continuous‐time nonlinear systems ( 2.73). In other words, if
is full‐rank, then the nonlinear system in ( 2.61) and ( 2.62) is locally weakly observable. It is worth noting that the observability matrix for continuous‐time linear systems ( 2.7) is a special case of the observability matrix for continuous‐time nonlinear systems ( 2.73). In other words, if 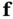 and
and 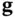 are linear functions, then ( 2.73) will be reduced to ( 2.7) [9, 24].
are linear functions, then ( 2.73) will be reduced to ( 2.7) [9, 24].
The nonlinear system in ( 2.61) and ( 2.62) can be linearized about 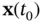 . Using Taylor series expansion and ignoring higher‐order terms, we will have the following linearized system:
. Using Taylor series expansion and ignoring higher‐order terms, we will have the following linearized system:
(2.74) 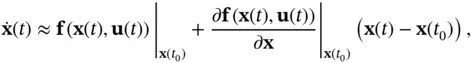
(2.75) 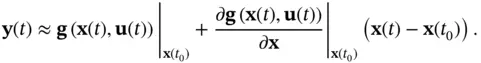
Then, the observability test for linear systems can be applied to the following linearized system matrices:
(2.76) 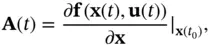
(2.77) 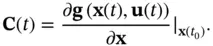
In this way, the nonlinear observability matrix in ( 2.73) can be approximated by the observability matrix, which is constructed using 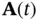 and
and 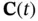 in ( 2.76) and ( 2.77). Although this approach may seem simpler, observability of the linearized system may not imply the observability of the original nonlinear system [9].
in ( 2.76) and ( 2.77). Although this approach may seem simpler, observability of the linearized system may not imply the observability of the original nonlinear system [9].
2.6.2 Discrete‐Time Nonlinear Systems
The state‐space model of a discrete‐time nonlinear system is represented by the following system of nonlinear equations:
(2.78) 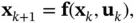
(2.79) 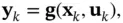
where 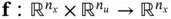 is the system function, and
is the system function, and 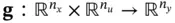 is the measurement function. Similar to the discrete‐time linear case, starting from the initial cycle, system's output vectors at successive cycles till cycle
is the measurement function. Similar to the discrete‐time linear case, starting from the initial cycle, system's output vectors at successive cycles till cycle 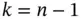 can be written based on the initial state
can be written based on the initial state 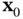 and input vectors
and input vectors 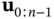 as follows:
as follows:
(2.80) 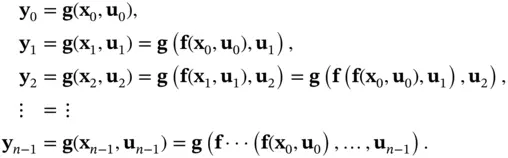
Functional powers of the system function  can be used to simplify the notation in the aforementioned equations. Functional powers are obtained by repeated composition of a function with itself:
can be used to simplify the notation in the aforementioned equations. Functional powers are obtained by repeated composition of a function with itself:
(2.81) 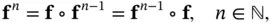
where 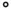 denotes the function‐composition operator:
denotes the function‐composition operator: 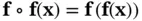 , and
, and 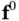 is the identity map. Alternatively, the difference equations in ( 2.80) can be rewritten as:
is the identity map. Alternatively, the difference equations in ( 2.80) can be rewritten as:
(2.82) 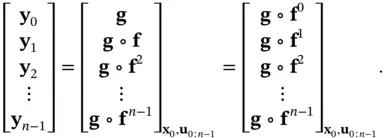
Similar to the continuous‐time case, the system of nonlinear difference equations in ( 2.82) can be linearized about the initial state 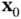 based on the Taylor series expansion to develop a linearized test for weak local observability of the nonlinear discrete‐time system ( 2.78) and ( 2.79). The nonlinear system in ( 2.78) and ( 2.79) is locally weakly observable at
based on the Taylor series expansion to develop a linearized test for weak local observability of the nonlinear discrete‐time system ( 2.78) and ( 2.79). The nonlinear system in ( 2.78) and ( 2.79) is locally weakly observable at 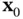 , if there exist a neighborhood of
, if there exist a neighborhood of 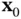 and an
and an 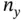 ‐tuple of integers
‐tuple of integers 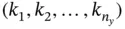 such that [9, 25]:
such that [9, 25]:
1 for .
2 The following observability matrix is full rank: (2.83)
where
(2.84) 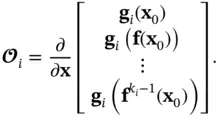
Читать дальше

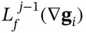 , an observability matrix can be constructed for the continuous‐time nonlinear system in ( 2.61) and ( 2.62) as follows:
, an observability matrix can be constructed for the continuous‐time nonlinear system in ( 2.61) and ( 2.62) as follows: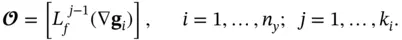
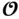 is full‐rank, then the nonlinear system in ( 2.61) and ( 2.62) is locally weakly observable. It is worth noting that the observability matrix for continuous‐time linear systems ( 2.7) is a special case of the observability matrix for continuous‐time nonlinear systems ( 2.73). In other words, if
is full‐rank, then the nonlinear system in ( 2.61) and ( 2.62) is locally weakly observable. It is worth noting that the observability matrix for continuous‐time linear systems ( 2.7) is a special case of the observability matrix for continuous‐time nonlinear systems ( 2.73). In other words, if 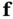 and
and 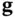 are linear functions, then ( 2.73) will be reduced to ( 2.7) [9, 24].
are linear functions, then ( 2.73) will be reduced to ( 2.7) [9, 24].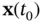 . Using Taylor series expansion and ignoring higher‐order terms, we will have the following linearized system:
. Using Taylor series expansion and ignoring higher‐order terms, we will have the following linearized system: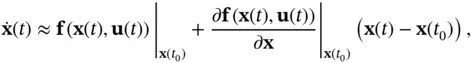
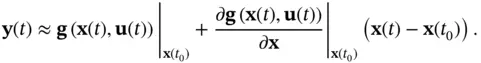
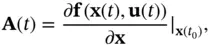
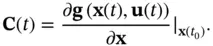
 and
and  in ( 2.76) and ( 2.77). Although this approach may seem simpler, observability of the linearized system may not imply the observability of the original nonlinear system [9].
in ( 2.76) and ( 2.77). Although this approach may seem simpler, observability of the linearized system may not imply the observability of the original nonlinear system [9].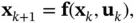
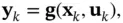
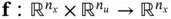 is the system function, and
is the system function, and 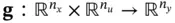 is the measurement function. Similar to the discrete‐time linear case, starting from the initial cycle, system's output vectors at successive cycles till cycle
is the measurement function. Similar to the discrete‐time linear case, starting from the initial cycle, system's output vectors at successive cycles till cycle 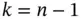 can be written based on the initial state
can be written based on the initial state 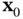 and input vectors
and input vectors 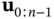 as follows:
as follows: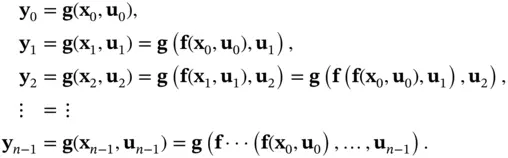
 can be used to simplify the notation in the aforementioned equations. Functional powers are obtained by repeated composition of a function with itself:
can be used to simplify the notation in the aforementioned equations. Functional powers are obtained by repeated composition of a function with itself: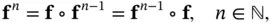
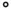 denotes the function‐composition operator:
denotes the function‐composition operator: 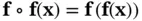 , and
, and 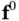 is the identity map. Alternatively, the difference equations in ( 2.80) can be rewritten as:
is the identity map. Alternatively, the difference equations in ( 2.80) can be rewritten as: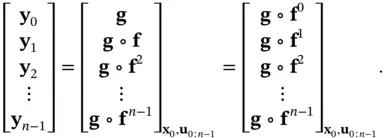
 based on the Taylor series expansion to develop a linearized test for weak local observability of the nonlinear discrete‐time system ( 2.78) and ( 2.79). The nonlinear system in ( 2.78) and ( 2.79) is locally weakly observable at
based on the Taylor series expansion to develop a linearized test for weak local observability of the nonlinear discrete‐time system ( 2.78) and ( 2.79). The nonlinear system in ( 2.78) and ( 2.79) is locally weakly observable at  , if there exist a neighborhood of
, if there exist a neighborhood of  and an
and an 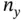 ‐tuple of integers
‐tuple of integers 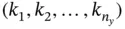 such that [9, 25]:
such that [9, 25]: