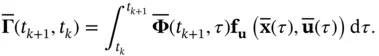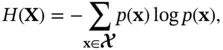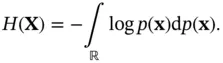The observability matrix for discrete‐time linear systems ( 2.22) is a special case of the observability matrix for discrete‐time nonlinear systems (2.83). In other words, if  and
and 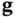 are linear functions, then (2.83) will be reduced to ( 2.22) [9, 25].
are linear functions, then (2.83) will be reduced to ( 2.22) [9, 25].
2.6.3 Discretization of Nonlinear Systems
Unlike linear systems, there is not a general functional representation for discrete‐time equivalents of continuous‐time nonlinear systems. One approach is to find a discrete‐time equivalent for the perturbed state‐space model of the nonlinear system under study [19]. In this approach, first, we need to linearize the nonlinear system in ( 2.61) and ( 2.62) about nominal values of state and input vectors, denoted by 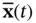 and
and 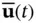 , respectively. The perturbation terms, denoted by
, respectively. The perturbation terms, denoted by 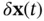 ,
, 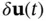 , and
, and 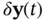 , are defined as the difference between the actual and the nominal values of state, input, and output vectors, respectively:
, are defined as the difference between the actual and the nominal values of state, input, and output vectors, respectively:
(2.85) 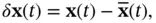
(2.86) 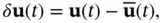
(2.87) 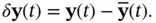
Since input is usually derived from a feedback control law, it may be a function of the state, 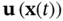 . In such cases, a difference between the actual and the nominal values of the state (a perturbation in the state) leads to a difference between the actual and the nominal values of the input (a perturbation in the input), and in effect therefore,
. In such cases, a difference between the actual and the nominal values of the state (a perturbation in the state) leads to a difference between the actual and the nominal values of the input (a perturbation in the input), and in effect therefore, 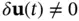 . Otherwise,
. Otherwise, 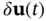 can be zero. Using the Taylor series expansion and neglecting the higher‐order terms, we obtain the following perturbation state‐space model:
can be zero. Using the Taylor series expansion and neglecting the higher‐order terms, we obtain the following perturbation state‐space model:
(2.88) 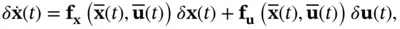
(2.89) 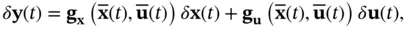
where 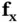 and
and 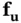 , respectively, denote the Jacobian matrices obtained by taking the derivatives of
, respectively, denote the Jacobian matrices obtained by taking the derivatives of 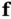 with respect to
with respect to 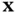 and
and  . Similarly,
. Similarly, 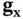 and
and 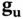 are Jacobians of
are Jacobians of 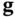 with respect to
with respect to 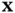 and
and 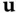 .
.
Now, the continuous‐time state‐space model in ( 2.88) and ( 2.89) can be treated as an LTV system. The discrete‐time equivalent of ( 2.88) and ( 2.89) is obtained as:
(2.90) 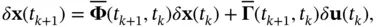
(2.91) 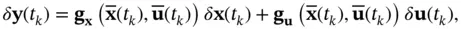
where 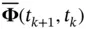 is the solution to
is the solution to
(2.92) 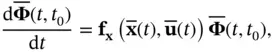
with the initial condition:
(2.93) 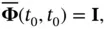
when we set 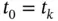 and
and 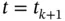 . As before,
. As before, 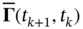 is given by:
is given by:
(2.94) 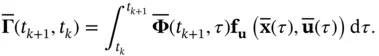
So far, this chapter has been focused on studying the observability of deterministic systems. Section 2.7discusses the observability of stochastic systems.
2.7 Observability of Stochastic Systems
Before proceeding with defining observability for stochastic systems, we need to recall a few concepts from information theory [26]:
Definition 2.3 Entropy is a measure of our uncertainty about an event in Shannon's information theory. Specifically, the entropy of a discrete random vector with alphabet is defined as:
(2.95) 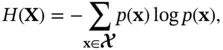
and correspondingly, for a continuous random vector , we have:
(2.96) 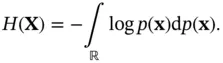
Читать дальше

 and
and  are linear functions, then (2.83) will be reduced to ( 2.22) [9, 25].
are linear functions, then (2.83) will be reduced to ( 2.22) [9, 25].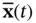 and
and 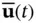 , respectively. The perturbation terms, denoted by
, respectively. The perturbation terms, denoted by 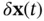 ,
, 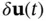 , and
, and 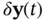 , are defined as the difference between the actual and the nominal values of state, input, and output vectors, respectively:
, are defined as the difference between the actual and the nominal values of state, input, and output vectors, respectively: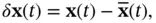
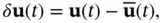
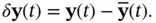
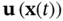 . In such cases, a difference between the actual and the nominal values of the state (a perturbation in the state) leads to a difference between the actual and the nominal values of the input (a perturbation in the input), and in effect therefore,
. In such cases, a difference between the actual and the nominal values of the state (a perturbation in the state) leads to a difference between the actual and the nominal values of the input (a perturbation in the input), and in effect therefore, 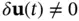 . Otherwise,
. Otherwise, 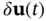 can be zero. Using the Taylor series expansion and neglecting the higher‐order terms, we obtain the following perturbation state‐space model:
can be zero. Using the Taylor series expansion and neglecting the higher‐order terms, we obtain the following perturbation state‐space model: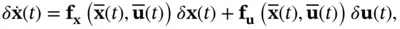
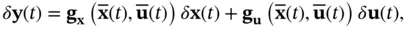
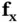 and
and 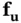 , respectively, denote the Jacobian matrices obtained by taking the derivatives of
, respectively, denote the Jacobian matrices obtained by taking the derivatives of 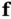 with respect to
with respect to 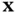 and
and  . Similarly,
. Similarly, 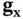 and
and 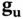 are Jacobians of
are Jacobians of 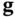 with respect to
with respect to 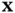 and
and 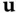 .
.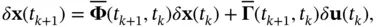
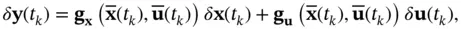
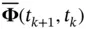 is the solution to
is the solution to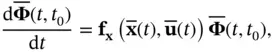
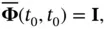
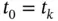 and
and 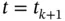 . As before,
. As before, 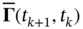 is given by:
is given by: