Simon Haykin - Nonlinear Filters
Здесь есть возможность читать онлайн «Simon Haykin - Nonlinear Filters» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на английском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Nonlinear Filters
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:5 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Nonlinear Filters: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Nonlinear Filters»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
Discover the utility of using deep learning and (deep) reinforcement learning in deriving filtering algorithms with this insightful and powerful new resource Nonlinear Filters: Theory and Applications
Nonlinear Filters
Nonlinear Filters: Theory and Applications

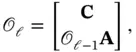
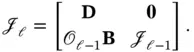
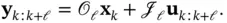
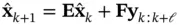
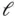 , if
, if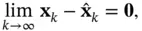
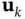 . Since the input is unknown, the observer equation ( 3.41) does not depend on the input. Moreover, the system outputs up to time step
. Since the input is unknown, the observer equation ( 3.41) does not depend on the input. Moreover, the system outputs up to time step 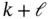 are used to estimate the state at time step
are used to estimate the state at time step 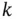 . Hence, the observer given by ( 3.41) is a delayed state estimator . Alternatively, it can be said that at time step
. Hence, the observer given by ( 3.41) is a delayed state estimator . Alternatively, it can be said that at time step 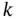 , the observer estimates the state at time step
, the observer estimates the state at time step 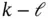 [35].
[35].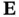 and
and 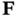 are chosen regarding the state estimation error:
are chosen regarding the state estimation error: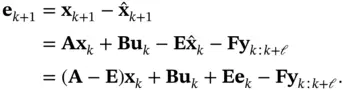
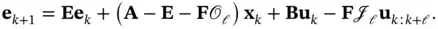
 to go to zero, regardless of the values of
to go to zero, regardless of the values of 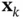 and
and 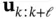 ,
, 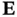 must be a Hurwitz matrix (its eigenvalues must be in the left‐half of the complex plane), and
must be a Hurwitz matrix (its eigenvalues must be in the left‐half of the complex plane), and 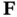 must simultaneously satisfy the following conditions:
must simultaneously satisfy the following conditions: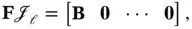
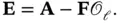
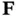 that satisfies condition ( 3.45) is guaranteed by the following theorem [35].
that satisfies condition ( 3.45) is guaranteed by the following theorem [35].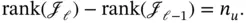
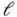 , which is a fairly strict condition. In the design phase, starting from
, which is a fairly strict condition. In the design phase, starting from  , the delay is increased until a value is found that satisfies ( 3.47). However,
, the delay is increased until a value is found that satisfies ( 3.47). However, 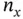 is an upper bound for
is an upper bound for 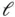 . To be more precise, if ( 3.47) is not satisfied for
. To be more precise, if ( 3.47) is not satisfied for 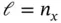 , then asymptotic state estimation will not be possible using the observer in ( 3.41).
, then asymptotic state estimation will not be possible using the observer in ( 3.41).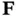 must be in the left nullspace of the last
must be in the left nullspace of the last 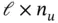 columns of
columns of 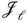 given by
given by  . Let
. Let 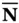 be a matrix whose rows form a basis for the left nullspace of
be a matrix whose rows form a basis for the left nullspace of 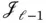 :
: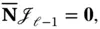
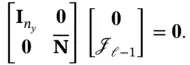
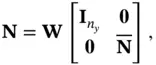
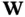 is an invertible matrix. Then, we have:
is an invertible matrix. Then, we have:










