1 ...6 7 8 10 11 12 ...41 In diesem Buch finden Sie am linken Rand einer Seite oft Symbole, die Sie auf eine besondere Stelle hinweisen. Ich verwende dabei sieben verschiedene Symbole, deren Bedeutung ich Ihnen hier erkläre.
 Mit diesem Symbol weise ich Sie auf eine Begriffserklärung hin. Üblicherweise steht es an der Stelle im Buch, an der der betreffende Begriff das erste Mal auftritt.
Mit diesem Symbol weise ich Sie auf eine Begriffserklärung hin. Üblicherweise steht es an der Stelle im Buch, an der der betreffende Begriff das erste Mal auftritt.
 Dieses Symbol steht für eine Gefahr: eine häufige Fehlerquelle, eine unerwartete Eigenschaft, eine Besonderheit oder Falle. Sie sollten solche Stellen extra aufmerksam lesen, um die Gefahr zu erkennen und nicht über solche Fallstricke zu stolpern.
Dieses Symbol steht für eine Gefahr: eine häufige Fehlerquelle, eine unerwartete Eigenschaft, eine Besonderheit oder Falle. Sie sollten solche Stellen extra aufmerksam lesen, um die Gefahr zu erkennen und nicht über solche Fallstricke zu stolpern.
 Dieses Symbol weist Sie auf einen Trick, eine besonders einfache, eine besonders wichtige Methode oder auf Eigenschaften hin, die Sie in der Ingenieurmathematik immer wieder gebrauchen können und beachten müssen.
Dieses Symbol weist Sie auf einen Trick, eine besonders einfache, eine besonders wichtige Methode oder auf Eigenschaften hin, die Sie in der Ingenieurmathematik immer wieder gebrauchen können und beachten müssen.
 Dieses Symbol lässt Sie einen Blick auf die tieferen mathematischen Zusammenhänge oder besondere Beispiele werfen. Meist werden Sie dabei schnell merken, dass die Sache technisch und kompliziert wird. Aber keine Sorge! Diese Dinge sind für den interessierten Leser gedacht. Falls Sie dabei etwas nicht sofort verstehen, können Sie einfach getrost darüber hinwegspringen. Für das weitere Verständnis sind diese Themen nicht wichtig.
Dieses Symbol lässt Sie einen Blick auf die tieferen mathematischen Zusammenhänge oder besondere Beispiele werfen. Meist werden Sie dabei schnell merken, dass die Sache technisch und kompliziert wird. Aber keine Sorge! Diese Dinge sind für den interessierten Leser gedacht. Falls Sie dabei etwas nicht sofort verstehen, können Sie einfach getrost darüber hinwegspringen. Für das weitere Verständnis sind diese Themen nicht wichtig.
 Dieses Symbol steht dort, wo ich Ihnen Hinweise zur praktischen Rechnung mit Hilfe des Mathematikprogramms »octave« gebe. Das Programm »octave« ist ein sehr nützliches Matlab-kompatibles Open-Source-Programm, das heißt, es ist für viele Betriebssysteme frei erhältlich. Der Umfang von octave ist wesentlich größer, als ich Ihnen im Rahmen dieses Buchs zeigen kann. Die mit diesem Symbol gekennzeichneten Stellen liefern Ihnen aber einen kleinen praktischen Einstieg. Falls Sie nicht daran interessiert sind, können Sie auch diese Stellen ohne Probleme einfach überspringen.
Dieses Symbol steht dort, wo ich Ihnen Hinweise zur praktischen Rechnung mit Hilfe des Mathematikprogramms »octave« gebe. Das Programm »octave« ist ein sehr nützliches Matlab-kompatibles Open-Source-Programm, das heißt, es ist für viele Betriebssysteme frei erhältlich. Der Umfang von octave ist wesentlich größer, als ich Ihnen im Rahmen dieses Buchs zeigen kann. Die mit diesem Symbol gekennzeichneten Stellen liefern Ihnen aber einen kleinen praktischen Einstieg. Falls Sie nicht daran interessiert sind, können Sie auch diese Stellen ohne Probleme einfach überspringen.
Sie können dieses Buch wie ein normales Buch verwenden und es von der ersten bis zur letzten Seite einfach durchlesen. Sie können aber auch anders vorgehen. Dieses Buch ist so aufgebaut, dass Sie seine Teile relativ unabhängig voneinander lesen oder zwischen einzelnen Themenbereichen hin und her springen können, um sich einen raschen Überblick zu verschaffen. Ich verweise an vielen Stellen auf die Abschnitte und Kapitel, in denen ein bestimmtes Thema ausführlich behandelt wird.
Allerdings hängen einige Kapitel grundlegend von anderen Kapiteln ab. Die vorgegebene Reihenfolge erleichtert Ihnen in diesen Fällen das Verständnis. Das betrifft natürlich das Kapitel 1, das die wichtigsten Grundlagen für alle folgenden Teile zusammenfasst. Ebenso sind die Kapitel 2und 3, die eine Einführung in die mehrdimensionale Differentialrechnung liefern, eine gute und wichtige Grundlage für Teil Iund Teil II.
Sie können aber Teil IIIund Teil IVnahezu problemlos in beliebiger Reihenfolge lesen oder auch ganz weglassen. Ebenso sind diese beiden Teile fast völlig unabhängig von den ersten beiden Teilen dieses Buchs, abgesehen von Kapitel 1. Die in Kapitel 1zusammengefassten Grundlagen aus der eindimensionalen Analysis und der Vektorrechnung sind für alle folgenden Kapitel wichtig. Werfen Sie daher mindestens einen Blick auf Kapitel 1, bevor Sie andere Teile lesen! Nur falls Ihnen die dort behandelten Themen geläufig sind, können Sie dieses Kapitel gefahrlos überspringen.
Teil I
Mehrdimensionale Analysis für Ingenieure

IN DIESEM TEIL …
Wie die eindimensionale Analysis beschäftigt sich auch die mehrdimensionale Analysis mit Funktionen und deren Stetigkeit, Differenzierbarkeit und Integration, allerdings nicht nur mit Funktionen einer reellen Variablen, sondern allgemeiner mit Funktionen mehrerer reeller Variablen oder Funktionen von reellen Vektoren.
Mehrdimensionale Funktionen sind bei der mathematischen Beschreibung realer technischer und naturwissenschaftlicher Systeme oft ein unerlässliches Hilfsmittel.
In diesem Teil werden Differentialrechnung und grundlegende Methoden sowohl der Optimierung als auch der Integration im Mehrdimensionalen dargestellt.
Kapitel 1
IN DIESEM KAPITEL
Bezeichnungen und Schreibweisen
Vektoren, Matrizen, Determinanten und lineare Gleichungssysteme
Das Wichtigste aus der eindimensionalen Analysis
Mehrdimensionale Analysis, gewöhnliche Differentialgleichungen, Funktionentheorie, stochastische Prozesse – das alles klingt nach fortgeschrittener Mathematik. Und das ist es auch. Die Themen dieses Buchs bauen auf mathematischen Methoden aus der linearen Algebra und der eindimensionalen Analysis auf. Naturgemäß können nicht alle Grundlagen ausführlich erläutert werden: Das Buch hätte dann mindestens den doppelten Umfang. Ich gehe daher davon aus, dass Sie den größten Teil der benötigten Grundlagenmathematik schon kennen. Dazu gehören die Grundbegriffe der mathematischen Sprache, neben den üblichen Rechensymbolen auch die logischen Zeichen 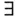 für »es existiert« und
für »es existiert« und 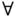 für »für alle«, das Zahlensystem der reellen Zahlen
für »für alle«, das Zahlensystem der reellen Zahlen 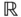 mit den darin enthaltenen natürlichen Zahlen
mit den darin enthaltenen natürlichen Zahlen 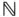 , den ganzen Zahlen
, den ganzen Zahlen 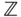 und den rationalen Zahlen
und den rationalen Zahlen 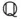 und die darauf aufbauende Vektorrechnung in den
und die darauf aufbauende Vektorrechnung in den 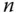 -dimensionalen Vektorräumen
-dimensionalen Vektorräumen 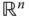 oder die eindimensionale Analysis.
oder die eindimensionale Analysis.
Keine Panik! Die für dieses Buch wichtigsten Begriffe und Methoden aus diesen Bereichen werde ich in diesem Kapitel kurz erläutern. Falls Sie darüber hinaus neugierig geworden sind, wie das alles im Detail aussieht, können Sie das zum Beispiel im ersten Band »Mathematik für Ingenieure 1 für Dummies« nachlesen.
Grundlagen aus der linearen Algebra
Das Rechnen mit Vektoren und Matrizen spielt für die mehrdimensionale Analysis eine ähnliche Rolle wie die Grundrechenarten für die eindimensionale Analysis. Anstelle der reellen Zahlen aus 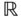 treten hierbei Vektoren als Variablen und Funktionswerte auf, und bei der Klassifizierung von Extremstellen helfen Ihnen bestimmte Eigenschaften von Matrizen weiter. Die bei der Optimierung häufig auftretenden, oft sehr schwierig zu lösenden nichtlinearen Gleichungssysteme können Sie mit Hilfe des Newton-Verfahrens durch die Lösungen linearer Gleichungssystemen zumindest approximieren. Grund genug, diese Grundlagen hier kurz zu wiederholen.
treten hierbei Vektoren als Variablen und Funktionswerte auf, und bei der Klassifizierung von Extremstellen helfen Ihnen bestimmte Eigenschaften von Matrizen weiter. Die bei der Optimierung häufig auftretenden, oft sehr schwierig zu lösenden nichtlinearen Gleichungssysteme können Sie mit Hilfe des Newton-Verfahrens durch die Lösungen linearer Gleichungssystemen zumindest approximieren. Grund genug, diese Grundlagen hier kurz zu wiederholen.
Читать дальше

 Mit diesem Symbol weise ich Sie auf eine Begriffserklärung hin. Üblicherweise steht es an der Stelle im Buch, an der der betreffende Begriff das erste Mal auftritt.
Mit diesem Symbol weise ich Sie auf eine Begriffserklärung hin. Üblicherweise steht es an der Stelle im Buch, an der der betreffende Begriff das erste Mal auftritt. Dieses Symbol steht für eine Gefahr: eine häufige Fehlerquelle, eine unerwartete Eigenschaft, eine Besonderheit oder Falle. Sie sollten solche Stellen extra aufmerksam lesen, um die Gefahr zu erkennen und nicht über solche Fallstricke zu stolpern.
Dieses Symbol steht für eine Gefahr: eine häufige Fehlerquelle, eine unerwartete Eigenschaft, eine Besonderheit oder Falle. Sie sollten solche Stellen extra aufmerksam lesen, um die Gefahr zu erkennen und nicht über solche Fallstricke zu stolpern. Dieses Symbol weist Sie auf einen Trick, eine besonders einfache, eine besonders wichtige Methode oder auf Eigenschaften hin, die Sie in der Ingenieurmathematik immer wieder gebrauchen können und beachten müssen.
Dieses Symbol weist Sie auf einen Trick, eine besonders einfache, eine besonders wichtige Methode oder auf Eigenschaften hin, die Sie in der Ingenieurmathematik immer wieder gebrauchen können und beachten müssen. Dieses Symbol lässt Sie einen Blick auf die tieferen mathematischen Zusammenhänge oder besondere Beispiele werfen. Meist werden Sie dabei schnell merken, dass die Sache technisch und kompliziert wird. Aber keine Sorge! Diese Dinge sind für den interessierten Leser gedacht. Falls Sie dabei etwas nicht sofort verstehen, können Sie einfach getrost darüber hinwegspringen. Für das weitere Verständnis sind diese Themen nicht wichtig.
Dieses Symbol lässt Sie einen Blick auf die tieferen mathematischen Zusammenhänge oder besondere Beispiele werfen. Meist werden Sie dabei schnell merken, dass die Sache technisch und kompliziert wird. Aber keine Sorge! Diese Dinge sind für den interessierten Leser gedacht. Falls Sie dabei etwas nicht sofort verstehen, können Sie einfach getrost darüber hinwegspringen. Für das weitere Verständnis sind diese Themen nicht wichtig. Dieses Symbol steht dort, wo ich Ihnen Hinweise zur praktischen Rechnung mit Hilfe des Mathematikprogramms »octave« gebe. Das Programm »octave« ist ein sehr nützliches Matlab-kompatibles Open-Source-Programm, das heißt, es ist für viele Betriebssysteme frei erhältlich. Der Umfang von octave ist wesentlich größer, als ich Ihnen im Rahmen dieses Buchs zeigen kann. Die mit diesem Symbol gekennzeichneten Stellen liefern Ihnen aber einen kleinen praktischen Einstieg. Falls Sie nicht daran interessiert sind, können Sie auch diese Stellen ohne Probleme einfach überspringen.
Dieses Symbol steht dort, wo ich Ihnen Hinweise zur praktischen Rechnung mit Hilfe des Mathematikprogramms »octave« gebe. Das Programm »octave« ist ein sehr nützliches Matlab-kompatibles Open-Source-Programm, das heißt, es ist für viele Betriebssysteme frei erhältlich. Der Umfang von octave ist wesentlich größer, als ich Ihnen im Rahmen dieses Buchs zeigen kann. Die mit diesem Symbol gekennzeichneten Stellen liefern Ihnen aber einen kleinen praktischen Einstieg. Falls Sie nicht daran interessiert sind, können Sie auch diese Stellen ohne Probleme einfach überspringen.
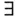 für »es existiert« und
für »es existiert« und 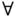 für »für alle«, das Zahlensystem der reellen Zahlen
für »für alle«, das Zahlensystem der reellen Zahlen 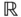 mit den darin enthaltenen natürlichen Zahlen
mit den darin enthaltenen natürlichen Zahlen 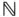 , den ganzen Zahlen
, den ganzen Zahlen 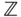 und den rationalen Zahlen
und den rationalen Zahlen 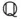 und die darauf aufbauende Vektorrechnung in den
und die darauf aufbauende Vektorrechnung in den 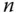 -dimensionalen Vektorräumen
-dimensionalen Vektorräumen 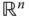 oder die eindimensionale Analysis.
oder die eindimensionale Analysis.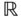 treten hierbei Vektoren als Variablen und Funktionswerte auf, und bei der Klassifizierung von Extremstellen helfen Ihnen bestimmte Eigenschaften von Matrizen weiter. Die bei der Optimierung häufig auftretenden, oft sehr schwierig zu lösenden nichtlinearen Gleichungssysteme können Sie mit Hilfe des Newton-Verfahrens durch die Lösungen linearer Gleichungssystemen zumindest approximieren. Grund genug, diese Grundlagen hier kurz zu wiederholen.
treten hierbei Vektoren als Variablen und Funktionswerte auf, und bei der Klassifizierung von Extremstellen helfen Ihnen bestimmte Eigenschaften von Matrizen weiter. Die bei der Optimierung häufig auftretenden, oft sehr schwierig zu lösenden nichtlinearen Gleichungssysteme können Sie mit Hilfe des Newton-Verfahrens durch die Lösungen linearer Gleichungssystemen zumindest approximieren. Grund genug, diese Grundlagen hier kurz zu wiederholen.










