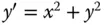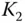7 Kapitel 7Abbildung 7.1: Die Kurven zu einem differenzierbaren (rechts) und e...Abbildung 7.2: Die Fläche zwischen dem Graphen des Skalarfelds 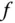 un...Abbildung 7.3: Approximation der Fläche zwischen
un...Abbildung 7.3: Approximation der Fläche zwischen 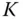 und dem Graphen ...Abbildung 7.4: Eine KorkenzieherlinieAbbildung 7.5: Eine Lemniskate mit dem Doppelpunkt
und dem Graphen ...Abbildung 7.4: Eine KorkenzieherlinieAbbildung 7.5: Eine Lemniskate mit dem Doppelpunkt 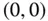 Abbildung 7.6: Ein einfach zusammenhängendes 2D-Gebiet (links) und ...Abbildung 7.7: Einfach zusammenhängende 3D-Gebiete (links) und nich...
Abbildung 7.6: Ein einfach zusammenhängendes 2D-Gebiet (links) und ...Abbildung 7.7: Einfach zusammenhängende 3D-Gebiete (links) und nich...
8 Kapitel 8Abbildung 8.1: Eine HalbkugelschaleAbbildung 8.2: Ein Torus ist nicht als Graph darstellbarAbbildung 8.3: Ein Torus kann parametrisiert werdenAbbildung 8.4: Parameterlinien (links) und Tangentialebene (rechts)...Abbildung 8.5: Das Paraboloid ist ein GraphAbbildung 8.6: Eine DrehflächeAbbildung 8.7: Die Mantelfläche eines Kegelstumpfs ist eine Drehflä...Abbildung 8.8: Eine Aufteilung des Parameterbereichs 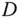 in Teilstück...Abbildung 8.9: … führt zu den Flächenstücken
in Teilstück...Abbildung 8.9: … führt zu den Flächenstücken 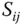 Abbildung 8.10: Lineare Taylor-Approximation der Parametrisierung ...Abbildung 8.11: Eine stationäre Strömung durch die Fläche
Abbildung 8.10: Lineare Taylor-Approximation der Parametrisierung ...Abbildung 8.11: Eine stationäre Strömung durch die Fläche 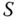
9 Kapitel 9Abbildung 9.1: Ein rotierendes VektorfeldAbbildung 9.2: Ein Moebiusband ist nicht orientierbarAbbildung 9.3: Das Normaleneinheitsvektorfeld eines Moebiusbands mu...Abbildung 9.4: Diese Kurve umläuft die eingeschlos sene Fläche mit ...
10 Kapitel 10Abbildung 10.1: Die Lösung 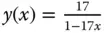 hat eine PolstelleAbbildung 10.2: Das Richtungsfeld zur Differentialgleichung
hat eine PolstelleAbbildung 10.2: Das Richtungsfeld zur Differentialgleichung 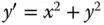 Abbildung 10.3: Die Isoklinen zur Differentialgleichung
Abbildung 10.3: Die Isoklinen zur Differentialgleichung 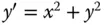
11 Kapitel 13Abbildung 13.1: Drei Lösungen der Eulerschen Differentialgleichung...
12 Kapitel 14Abbildung 14.1: Die Lösungskurve des Räuber-Beute-Modells zu den P...
13 Kapitel 17Abbildung 17.1: Integrationsweg 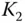
1 Cover
2 Titelblatt
3 Impressum Mathematik für Ingenieure II für Dummies Bibliografische Information der Deutschen Nationalbibliothek Die Deutsche Nationalbibliothek verzeichnet diese Publikation in der Deutschen Nationalbibliografie;detaillierte bibliografische Daten sind im Internet über http://dnb.d-nb.de abrufbar. 2. Auflage 2022 © 2022 Wiley-VCH GmbH, Boschstraße 12, 69469 Weinheim, Germany All rights reserved including the right of reproduction in whole or in part in any form. This book published by arrangement with John Wiley and Sons, Inc. Alle Rechte vorbehalten, inklusive des Rechtes auf Reproduktion im Ganzen oder in Teilen und in jeglicher Form. Dieses Buch wird mit Genehmigung von John Wiley and Sons, Inc. publiziert. Wiley, the Wiley logo, Für Dummies, the Dummies Man logo, and related trademarks and trade dress are trademarks or registered trademarks of John Wiley & Sons, Inc. and/or its affiliates, in the United States and other countries. Used by permission. Wiley, die Bezeichnung »Für Dummies«, das Dummies-Mann-Logo und darauf bezogene Gestaltungen sind Marken oder eingetragene Marken von John Wiley & Sons, Inc., USA, Deutschland und in anderen Ländern. Das vorliegende Werk wurde sorgfältig erarbeitet. Dennoch übernehmen Autoren und Verlag für die Richtigkeit von Angaben, Hinweisen und Ratschlägen sowie eventuelle Druckfehler keine Haftung. Coverfoto: © alphaspirit – stock.adobe.com Korrektur: Birgit Volk, Dr. Marianne Hammer-Altmann Print ISBN: 978-3-527-71988-4 ePub ISBN: 978-3-527-83910-0
4 Über den Autor Über den Autor Dr. J. Michael Fried studierte Mathematik und Physik zunächst an der Universität Heidelberg, dann an der Universität Freiburg und promovierte dort mit einem Thema aus der angewandten Mathematik. Nach einem Jahr an der Australian National University in Canberra ist Michael Fried heute Akademischer Direktor an der Universität Erlangen und unterrichtet dort Mathematik für Ingenieure und Physiker. Außerdem gibt er Kurse in angewandter Mathematik für Mathematikstudenten und arbeitet zusammen mit Mathematikern und Ingenieuren an verschiedenen Projekten im Bereich der mathematischen Bildverarbeitung. Für seinen Kurs zur Mathematik für Ingenieure wurde er mit dem Preis für gute Lehre 2009 des Freistaats Bayern ausgezeichnet.
5 Inhaltsverzeichnis
6 Einleitung Einleitung In den ersten Semestern eines ingenieurwissenschaftlichen Studiums begegnet Ihnen wahrscheinlich wesentlich mehr Mathematik, als Sie dies in Schulzeiten, außerhalb des Grundstudiums oder nach dem Studium jemals wieder erleben werden. Dies führt direkt zu der Frage, wozu so viel Mathematik für angehende Ingenieure notwendig sein mag, insbesondere wenn die meisten nach dem Abschluss des Studiums kaum noch direkt mit höherer Mathematik konfrontiert werden. Wozu sollen Sie Ihre wertvolle Zeit mit dem Lösen von Mathematikaufgaben und dem Durchdenken und Verstehen mathematischer Fragestellungen füllen? Der tiefere Grund für die ganze Mathematik ist: Ingenieure müssen logisch und analytisch sauber denken können. Und nirgendwo tritt dieses analytische Denken so klar zu Tage wie in der Mathematik. Eigentlich ist Mathematik nichts anderes als analytisches Denken. Mathematik ist abstrakt. Darüber kann man zwar wunderbar streiten (insbesondere mit angewandten Mathematikern), aber eigentlich macht gerade das ihre Stärke aus: die Konzentration auf das Wesentliche, die Analyse. Das systematische Zerlegen in die einzelnen Bestandteile, alles »Beiwerk« wegzulassen, bis nur noch der Kern der Sache vorhanden ist. Schließlich die Fähigkeit, die so erworbenen Kenntnisse auf andere, prinzipiell ähnliche Situationen anzuwenden.
7 Fangen Sie an zu lesen
8 Abbildungsverzeichnis
9 Stichwortverzeichnis
10 End User License Agreement
1 1
2 2
3 5
4 6
5 7
6 19
7 20
8 21
9 22
10 23
11 24
12 25
13 26
14 27
15 28
16 29
17 30
18 31
19 32
20 33
21 34
22 35
23 36
24 37
25 38
26 39
27 40
28 41
29 42
30 43
31 44
32 45
33 46
34 47
35 48
36 49
37 50
38 51
39 52
40 53
41 54
42 55
43 56
44 57
45 58
46 59
47 60
48 61
49 62
50 63
51 64
52 65
53 66
54 67
55 68
56 69
57 70
58 71
59 72
60 73
61 74
62 75
Читать дальше

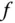 un...Abbildung 7.3: Approximation der Fläche zwischen
un...Abbildung 7.3: Approximation der Fläche zwischen 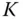 und dem Graphen ...Abbildung 7.4: Eine KorkenzieherlinieAbbildung 7.5: Eine Lemniskate mit dem Doppelpunkt
und dem Graphen ...Abbildung 7.4: Eine KorkenzieherlinieAbbildung 7.5: Eine Lemniskate mit dem Doppelpunkt 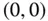 Abbildung 7.6: Ein einfach zusammenhängendes 2D-Gebiet (links) und ...Abbildung 7.7: Einfach zusammenhängende 3D-Gebiete (links) und nich...
Abbildung 7.6: Ein einfach zusammenhängendes 2D-Gebiet (links) und ...Abbildung 7.7: Einfach zusammenhängende 3D-Gebiete (links) und nich...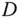 in Teilstück...Abbildung 8.9: … führt zu den Flächenstücken
in Teilstück...Abbildung 8.9: … führt zu den Flächenstücken 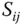 Abbildung 8.10: Lineare Taylor-Approximation der Parametrisierung ...Abbildung 8.11: Eine stationäre Strömung durch die Fläche
Abbildung 8.10: Lineare Taylor-Approximation der Parametrisierung ...Abbildung 8.11: Eine stationäre Strömung durch die Fläche 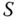
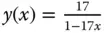 hat eine PolstelleAbbildung 10.2: Das Richtungsfeld zur Differentialgleichung
hat eine PolstelleAbbildung 10.2: Das Richtungsfeld zur Differentialgleichung 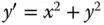 Abbildung 10.3: Die Isoklinen zur Differentialgleichung
Abbildung 10.3: Die Isoklinen zur Differentialgleichung