Lineare Gleichungssysteme und das Gauß-Verfahren
Lineare Gleichungssysteme, kurz LGS, treten bei vielen mathematischen Fragestellungen auf. Beispielsweise müssen Sie beim in Kapitel 4behandelten Newton-Verfahren zur Approximation von Nullstellen einer mehrdimensionalen Funktion in jedem Schritt ein LGS lösen. Ein LGS können Sie formal als
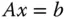
mit der Systemmatrix 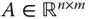 , dem gesuchten Vektor
, dem gesuchten Vektor 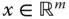 und dem Vektor der rechten Seite
und dem Vektor der rechten Seite  schreiben. Die meisten LGS, die in diesem Buch vorkommen werden, sind quadratische LGS , das heißt:
schreiben. Die meisten LGS, die in diesem Buch vorkommen werden, sind quadratische LGS , das heißt: 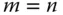 . Die Systemmatrix
. Die Systemmatrix  ist also quadratisch, und die beiden Vektoren
ist also quadratisch, und die beiden Vektoren  und
und 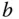 gehören demselben Vektorraum
gehören demselben Vektorraum 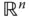 an.
an.
Manchmal empfiehlt es sich, ein LGS zuerst auf Lösbarkeit zu untersuchen, bevor Sie versuchen, die Lösung zu berechnen. Dies können Sie für quadratische LGS beispielsweise mit Hilfe der sogenannten Determinante 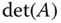 der Systemmatrix
der Systemmatrix 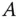 machen. Die eigentliche mathematische Definition der Determinanten ist etwas kompliziert, allerdings reicht es aus, eine Berechnungsvorschrift für Determinanten anzugeben.
machen. Die eigentliche mathematische Definition der Determinanten ist etwas kompliziert, allerdings reicht es aus, eine Berechnungsvorschrift für Determinanten anzugeben.
 Für eine quadratische Matrix
Für eine quadratische Matrix  mit
mit
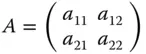
heißt die Zahl
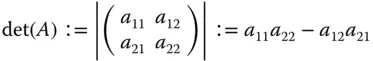
die Determinante von  . Für eine Matrix
. Für eine Matrix  ist
ist
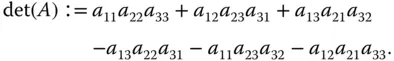
Determinanten für Matrizen mit mehr als drei Zeilen und Spalten berechnen Sie mit Hilfe des sogenannten Laplaceschen Entwicklungssatzes über die Kofaktoren bestimmter Matrixkomponenten.
 Ist
Ist  eine quadratische Matrix mit
eine quadratische Matrix mit 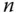 Zeilen und Spalten, dann heißt die quadratische Matrix mit
Zeilen und Spalten, dann heißt die quadratische Matrix mit  Zeilen und Spalten, die aus
Zeilen und Spalten, die aus 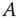 durch Streichen der
durch Streichen der 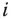 -ten Zeile und der
-ten Zeile und der 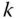 -ten Spalte entsteht, die Untermatrix
-ten Spalte entsteht, die Untermatrix 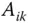 .
.
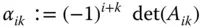
heißt der Kofaktor zum Element 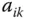 der Matrix
der Matrix 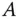 .
.
Mit Hilfe von Untermatrizen lassen sich ganz allgemein Determinanten auf zwei Weisen rekursiv berechnen.
Die eine Möglichkeit ist die Entwicklung nach der -ten Spalte : für ist:
Die andere Variante ist die Entwicklung nach der -ten Zeile : für ist:
Mit diesen beiden Methoden können Sie die Berechnung der Determinante jeder quadratischen Matrix  auf die Berechnung von Determinanten quadratischer Matrizen mit nur zwei Zeilen und Spalten zurückführen.
auf die Berechnung von Determinanten quadratischer Matrizen mit nur zwei Zeilen und Spalten zurückführen.
Determinanten werden zum Beispiel bei der weiter unten in diesem Kapitel beschriebenen Eigenwertberechnung und bei der Transformation verschiedener Koordinatensysteme zur mehrdimensionalen Integration benötigt, die in Kapitel 6behandelt wird.
Außerdem können Sie mit Hilfe der Determinante der Systemmatrix die eindeutige Lösbarkeit eines quadratischen LGS feststellen.
 Ist für die Systemmatrix
Ist für die Systemmatrix  eines quadratischen LGS
eines quadratischen LGS
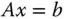
die Determinante 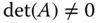 von null verschieden, dann existiert ein einziger Lösungsvektor
von null verschieden, dann existiert ein einziger Lösungsvektor 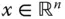 für dieses LGS. Ist dagegen
für dieses LGS. Ist dagegen 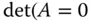 , dann gibt es entweder keine oder unendlich viele Lösungen des LGS.
, dann gibt es entweder keine oder unendlich viele Lösungen des LGS.
Читать дальше

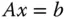
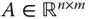 , dem gesuchten Vektor
, dem gesuchten Vektor 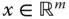 und dem Vektor der rechten Seite
und dem Vektor der rechten Seite  schreiben. Die meisten LGS, die in diesem Buch vorkommen werden, sind quadratische LGS , das heißt:
schreiben. Die meisten LGS, die in diesem Buch vorkommen werden, sind quadratische LGS , das heißt: 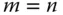 . Die Systemmatrix
. Die Systemmatrix  ist also quadratisch, und die beiden Vektoren
ist also quadratisch, und die beiden Vektoren  und
und 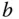 gehören demselben Vektorraum
gehören demselben Vektorraum 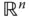 an.
an.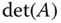 der Systemmatrix
der Systemmatrix 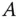 machen. Die eigentliche mathematische Definition der Determinanten ist etwas kompliziert, allerdings reicht es aus, eine Berechnungsvorschrift für Determinanten anzugeben.
machen. Die eigentliche mathematische Definition der Determinanten ist etwas kompliziert, allerdings reicht es aus, eine Berechnungsvorschrift für Determinanten anzugeben. Für eine quadratische Matrix
Für eine quadratische Matrix  mit
mit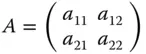
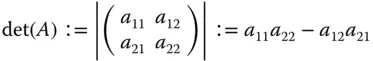
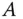 . Für eine Matrix
. Für eine Matrix  ist
ist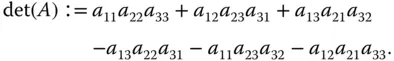
 eine quadratische Matrix mit
eine quadratische Matrix mit 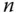 Zeilen und Spalten, dann heißt die quadratische Matrix mit
Zeilen und Spalten, dann heißt die quadratische Matrix mit  Zeilen und Spalten, die aus
Zeilen und Spalten, die aus 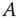 durch Streichen der
durch Streichen der 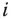 -ten Zeile und der
-ten Zeile und der 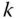 -ten Spalte entsteht, die Untermatrix
-ten Spalte entsteht, die Untermatrix 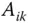 .
.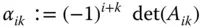
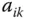 der Matrix
der Matrix 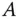 .
. auf die Berechnung von Determinanten quadratischer Matrizen mit nur zwei Zeilen und Spalten zurückführen.
auf die Berechnung von Determinanten quadratischer Matrizen mit nur zwei Zeilen und Spalten zurückführen. Ist für die Systemmatrix
Ist für die Systemmatrix  eines quadratischen LGS
eines quadratischen LGS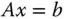
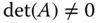 von null verschieden, dann existiert ein einziger Lösungsvektor
von null verschieden, dann existiert ein einziger Lösungsvektor 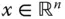 für dieses LGS. Ist dagegen
für dieses LGS. Ist dagegen 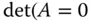 , dann gibt es entweder keine oder unendlich viele Lösungen des LGS.
, dann gibt es entweder keine oder unendlich viele Lösungen des LGS.










