Es gibt sehr viele verschiedene Verfahren zur exakten oder näherungsweisen Lösung eines LGS. Die meisten dieser Verfahren eignen sich hauptsächlich für die computergestützte Lösung sehr großer LGS, das heißt für eine sehr große Zahl von Unbekannten und Gleichungen.
Einige Verfahren können Sie aber durchaus auch zur Berechnung der Lösung kleinerer LGS von Hand einsetzen. Das bekannteste und wichtigste dieser Verfahren ist der Gauß-Algorithmus. Die zugrunde liegende Idee ist es, das zu lösende Gleichungssystem auf obere Dreiecksgestalt zu bringen und dann die Lösung durch Rückwärtslösen zu bestimmen.
Ist beispielsweise 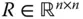 eine obere Dreiecksmatrix :
eine obere Dreiecksmatrix :

mit
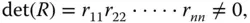
dann ist die Lösung des LGS 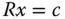 eindeutig bestimmt, und das Rückwärtslösen können Sie nach dem folgenden Algorithmus vornehmen:
eindeutig bestimmt, und das Rückwärtslösen können Sie nach dem folgenden Algorithmus vornehmen:
1 Starten Sie in der -ten Zeile:
2 Weiter geht es mit der -ten Zeile:Diese können Sie nach auflösen, da Sie schon aus dem letzten Schritt kennen.
3 Auf diese Weise arbeiten Sie sich rückwärts von unten nach oben durch die einzelnen Zeilen des gestaffelten Systems.In der -ten Zeile sieht das so aus:
Zur Lösung eines beliebigen LGS 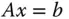 mit
mit 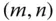 -Matrix
-Matrix 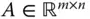 und rechter Seite
und rechter Seite  wird, wenn möglich, beim Gauß-Algorithmus das LGS durch geeignete elementare Zeilenumformungen zu einem LGS
wird, wenn möglich, beim Gauß-Algorithmus das LGS durch geeignete elementare Zeilenumformungen zu einem LGS 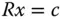 mit Dreiecksmatrix
mit Dreiecksmatrix 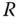 und mit neuer rechter Seite
und mit neuer rechter Seite 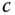 umgeformt, welches dieselbe Lösung wie das ursprüngliche System besitzt.
umgeformt, welches dieselbe Lösung wie das ursprüngliche System besitzt.
Die erlaubten elementaren Zeilenumformungen sind dabei:
Multiplikation einer Zeile mit einem Skalar :
Vertauschung zweier Zeilen
Addition eines Vielfachen einer Zeile zu einer anderen Zeile:
Mit Hilfe der obigen Zeilenumformungen führen Sie die Gauß-Elimination so durch:
1 Bilden Sie die erweiterte Systemmatrix , indem Sie die Matrix rechts um eine Spalte mit dem Rechte-Seite-Vektor erweitern. Setzen Sie .Nach jedem der folgenden Schritte erhalten Sie eine neue erweiterte Systemmatrix, die Sie aber der Übersichtlichkeit halber wieder mit bezeichnen. Genauso bezeichnen Sie auch die neuen Komponenten wieder mit .
2 Ist die Komponente , dann tauschen Sie eine Zeile mit der erweiterten Systemmatrix mit der Zeile . Falls es unterhalb der -ten Zeile keine Zeile mit gibt, sind Sie fertig und gehen zu Schritt 7.Prinzipiell ist es gleichgültig, durch welche Zeile Sie dabei die -te Zeile ersetzen, solange nach dem Tausch die Komponente ist. Bei der praktischen Rechnung wählen Sie hier möglichst eine Zeile mit Komponente .
3 Putzen Sie unterhalb der -ten Zeile die -e Spalte, indem Sie zu jeder Zeile mit das -Fache der -ten Zeile addieren.Sie bearbeiten also nur die Zeilen unterhalb der -ten Zeile und erhalten eine neue erweiterte Systemmatrix, bei der in der -ten Spalte unterhalb der Diagonalkomponente nur noch Nullen stehen.
4 Setzen Sie .
5 Ist , dann sind Sie fertig und gehen zu Schritt 7.
6 Gehen Sie zu Schritt 2, und fahren Sie dort fort.Falls Sie nicht vorher zu Schritt 7 springen, dann wiederholen Sie diesen Algorithmus Zeile für Zeile, bis Sie in der letzten Zeile angekommen sind.
7 Beenden Sie die Elimination.
Mit diesem Eliminationsalgorithmus bringen Sie die erweiterte Matrix 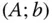 auf die folgende Gestalt:
auf die folgende Gestalt:

 Die Zahl
Die Zahl 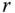 wird Rang der Matrix
wird Rang der Matrix 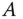 genannt.
genannt.
In den ersten 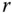 Zeilen ist dies ein gestaffeltes Gleichungssystem. Hier stehen »Leerzeichen« für die Null und
Zeilen ist dies ein gestaffeltes Gleichungssystem. Hier stehen »Leerzeichen« für die Null und  und
und 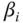 für irgendwelche Zahlen. Ist
für irgendwelche Zahlen. Ist 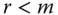 , dann treten in der neu erhaltenen Matrix
, dann treten in der neu erhaltenen Matrix 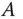 reine Nullzeilen auf, während auf der neuen rechten Seite
reine Nullzeilen auf, während auf der neuen rechten Seite 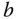 in diesen Zeilen eventuell auch andere Zahlen auftauchen können.
in diesen Zeilen eventuell auch andere Zahlen auftauchen können.
Für die Lösbarkeit des LGS 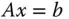 gilt:
gilt:
Nicht lösbar, falls die Zahlen nicht alle gleich null sind.
Nicht eindeutig lösbar, falls ist, das heißt, falls alle sind. Die Unbekannten können frei gewählt werden. Die restlichen Unbekannten ergeben sich dann eindeutig aus den frei gewählten Unbekannten.
Eindeutig lösbar, falls ist. Die Lösung erhalten Sie durch Rückwärtslösen.
Eigenwerte, Eigenvektoren und die Definitheit von Matrizen
Wie im Abschnitt »Ganz sicher: Hinreichende Optimalitätsbedingung« aus Kapitel 5dargestellt wird, spielt bei der Untersuchung auf Extremstellen mehrdimensionaler Funktionen die Definitheit von symmetrischen Matrizen eine ähnlich wesentliche Rolle wie das Vorzeichen der zweiten Ableitung für eindimensionale Funktionen.
 Eine symmetrische
Eine symmetrische 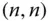 -Matrix
-Matrix 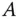 heißt:
heißt:
Читать дальше

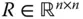 eine obere Dreiecksmatrix :
eine obere Dreiecksmatrix :
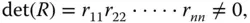
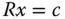 eindeutig bestimmt, und das Rückwärtslösen können Sie nach dem folgenden Algorithmus vornehmen:
eindeutig bestimmt, und das Rückwärtslösen können Sie nach dem folgenden Algorithmus vornehmen: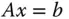 mit
mit 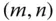 -Matrix
-Matrix 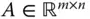 und rechter Seite
und rechter Seite  wird, wenn möglich, beim Gauß-Algorithmus das LGS durch geeignete elementare Zeilenumformungen zu einem LGS
wird, wenn möglich, beim Gauß-Algorithmus das LGS durch geeignete elementare Zeilenumformungen zu einem LGS 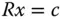 mit Dreiecksmatrix
mit Dreiecksmatrix 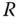 und mit neuer rechter Seite
und mit neuer rechter Seite 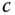 umgeformt, welches dieselbe Lösung wie das ursprüngliche System besitzt.
umgeformt, welches dieselbe Lösung wie das ursprüngliche System besitzt.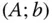 auf die folgende Gestalt:
auf die folgende Gestalt:
 Die Zahl
Die Zahl 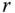 wird Rang der Matrix
wird Rang der Matrix 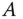 genannt.
genannt.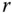 Zeilen ist dies ein gestaffeltes Gleichungssystem. Hier stehen »Leerzeichen« für die Null und
Zeilen ist dies ein gestaffeltes Gleichungssystem. Hier stehen »Leerzeichen« für die Null und  und
und 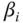 für irgendwelche Zahlen. Ist
für irgendwelche Zahlen. Ist 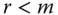 , dann treten in der neu erhaltenen Matrix
, dann treten in der neu erhaltenen Matrix 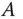 reine Nullzeilen auf, während auf der neuen rechten Seite
reine Nullzeilen auf, während auf der neuen rechten Seite 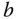 in diesen Zeilen eventuell auch andere Zahlen auftauchen können.
in diesen Zeilen eventuell auch andere Zahlen auftauchen können.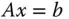 gilt:
gilt: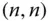 -Matrix
-Matrix 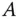 heißt:
heißt:










