J. Michael Fried - Mathematik für Ingenieure II für Dummies

Sind und linear unabhängig, so bilden und eine positiv orientierte Basis.

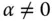Ist der Winkel zwischen den beiden linear unabhängigen Vektoren 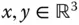, dann gilt: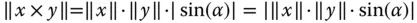

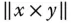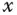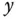Die Länge des Kreuzprodukts entspricht also dem Flächeninhalt des durch und aufgespannten Parallelogramms.

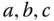Drei beliebige Vektoren des 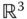spannen einen Spat auf. Dieser Körper ähnelt einem schiefen Backstein, ein Beispiel ist in Abbildung 1.1dargestellt. Für die drei Vektoren 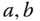und 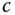heißt die durch 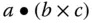definierte reelle Zahl das Spatprodukt aus 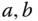und .

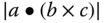Der Absolutbetrag entspricht dem Volumen des Spats.

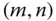Neben den Vektoren sind reelle -Matrizen 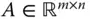mit 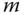Zeilen und 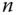Spalten weitere mathematische Objekte aus der linearen Algebra, die bei der mehrdimensionalen Analysis eine wichtige Rolle spielen.

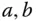Abbildung 1.1: Ein Spat oder Parallelepiped, das durch die drei Vektoren und 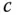aufgespannt wird

Matrizen können Sie als Vektoren auffassen, und genau wie bei Spalten- oder Zeilenvektoren können Sie auch Matrizen derselben Dimension komponentenweise addieren oder mit einer reellen Zahl multiplizieren. Zwei Matrizen, bei denen die Spaltenzahl der ersten Matrix mit der Zeilenzahl der zweiten Matrix übereinstimmt, können Sie nach der folgenden Definition auch miteinander multiplizieren.

Ist 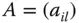eine reelle 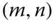-Matrix und 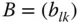eine reelle 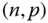-Matrix, dann heißt die 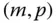-Matrix 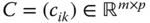mit den Komponenten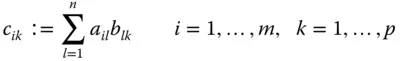

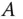das Produkt von und .

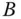Das Standardskalarprodukt der Spaltenvektoren können Sie als ein besonderes Matrizenprodukt interpretieren: Betrachten Sie die beiden Spaltenvektoren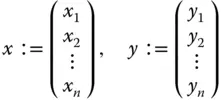

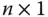als -Matrizen und definieren Sie zum Spaltenvektor den Zeilenvektor 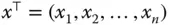, eine einzeilige und -spaltigen Matrix. Das Skalarprodukt 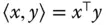ist dann das Matrizenprodukt aus der -Matrix 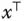und der 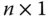-Matrix .