Törichte Annahmen über den Leser
Das vorliegende Buch ist in einem gewissen Sinne der zweite Band einer Einführung in die Ingenieurmathematik. Trotzdem setzte ich nicht grundsätzlich voraus, dass Sie das erste Buch oder die dort behandelten mathematischen Themen kennen, sondern gebe Ihnen im ersten Kapitel einen kurzen Überblick über die wichtigsten Grundlagen. Allerdings gehe ich stillschweigend doch davon aus, dass der Leser zumindest eine Ahnung von der üblichen Schulmathematik hat.
Sie sollten:
ein paar Grundkenntnisse aus der Algebra wie zum Beispiel Bruchrechnen und die binomischen Formeln mitbringen.Kopfrechnen ist lästig, und in Zeiten von Handys mit eingebauten Taschenrechnern und ausgefeilten Computeralgebraprogrammen sieht nicht jeder unbedingt ein, dass es sich dabei um eine nützliche Fähigkeit handelt. Allerdings können Sie die beschriebenen Beispiele wesentlich schneller und einfacher verfolgen, wenn Sie nicht bei jeder kleinen Rechnung zu einer Rechenhilfe greifen müssen.
eine Ahnung von den Grundbegriffen der Vektorrechnung und eindimensionalen Analysis haben.Falls Ihre Kenntnisse dazu doch ein wenig verstaubt sind, bietet Ihnen das Kapitel 1»Was bisher geschah« zu Beginn des ersten Teils eine kurze Wiederholung.
versuchen, die Beispiele selbstständig nachzurechnen.Mit der Mathematik ist es wie mit jeder Kunst: Sie können sie nur dann völlig begreifen, wenn Sie auch praktisch damit umgehen. Eine Möglichkeit dazu besteht darin, die Beispiele nicht einfach nur nachzulesen, sondern sich selbst am einen oder anderen zu versuchen. Am besten bevor Sie den im Buch beschriebenen Lösungsweg nachlesen.
Wie dieses Buch aufgebaut ist
Dieses Buch ist in Teile unterteilt, die einzelnen Teile sind in Kapitel gegliedert, die ihrerseits aus Abschnitten und Unterabschnitten bestehen. Die Teile fassen dabei die einzelnen Themenbereiche zusammen, und die Kapitel eines Teils behandeln jeweils ein wesentliches Thema aus dem entsprechenden Bereich.
Teil I: Mehrdimensionale Analysis für Ingenieure
Neben einer kurzen Zusammenfassung der wichtigsten Methoden der eindimensionalen Analysis, Vektor- und Matrizenrechnung behandelt Teil Idie Grundlagen der Differentialrechnung im Mehrdimensionalen.
Das erste Kapitel liefert Ihnen dabei die Grundlagen für alle folgenden Themen des gesamten Buchs, nicht nur für Teil 1.
Wie in der eindimensionalen Analysis ist die Untersuchung des Änderungsverhaltens einer gegebenen Funktion auch eine der wichtigen Standardaufgaben der mehrdimensionalen Analysis. Im Unterschied zur eindimensionalen Analysis können die Variablen und die Funktionswerte hier aber mehrdimensionale Vektoren sein. Dies erfordert zum einen eine Verallgemeinerung der Begriffe aus der eindimensionalen Differentialrechnung, zum anderen auch ganz neue Begriffe und Methoden.
Kapitel 2und Kapitel 3stellen diese Begriffe und die grundlegenden Methoden der mehrdimensionalen Differentialrechnung dar und veranschaulichen diese durch viele Beispiele.
In Kapitel 4und Kapitel 5werden die zuvor dargestellten Methoden angewendet. Dabei beschreibt Kapitel 4drei spezielle mathematische Anwendungen, die auch in praktischen Situationen oft nützlich und hilfreich sein können, während sich Kapitel 5der mehrdimensionalen Optimierung widmet und die Frage nach Minima und Maxima mehrdimensionaler Funktionen beantwortet.
Teil II: Integralrechnung und Vektoranalysis
Der zweite Teil beschäftigt sich mit dem zweiten großen Teilgebiet der Analysis: der Integralrechnung. In der mehrdimensionalen Analysis ist die Integralrechnung wesentlich vielfältiger, als dies in der eindimensionalen Analysis der Fall ist. So können Sie eine Funktion nicht nur über 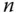 -dimensionale Teilmengen eines
-dimensionale Teilmengen eines 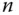 -dimensionalen Raums integrieren, sondern auch über niedriger dimensionale Teilmengen: Sie können Raum-, Flächen- und Kurvenintegrale definieren und berechnen. Die letzten beiden Sorten von Integralen unterscheiden sich noch einmal je nach Art der Integrandenfunktion: Vektorwertige Funktionen benötigen eine andere Art der Integration als skalarwertige Funktionen.
-dimensionalen Raums integrieren, sondern auch über niedriger dimensionale Teilmengen: Sie können Raum-, Flächen- und Kurvenintegrale definieren und berechnen. Die letzten beiden Sorten von Integralen unterscheiden sich noch einmal je nach Art der Integrandenfunktion: Vektorwertige Funktionen benötigen eine andere Art der Integration als skalarwertige Funktionen.
In Kapitel 6werden beispielhaft für allgemeine Raumintegrale solche Integrale im zwei- oder dreidimensionalen Raum behandelt. Dies entspricht einer Verallgemeinerung der Integration aus der eindimensionalen Analysis und lässt sich im Wesentlichen auf diese zurückführen.
Kapitel 7und Kapitel 8führen die beiden anderen Sorten von mehrdimensionalen Integralen ein: Kurvenintegrale und Flächenintegrale über Funktionen von zwei oder drei Variablen.
Kapitel 9liefert Ihnen einen kurzen Überblick über die Zusammenhänge, die zwischen den drei Integralsorten bestehen, und zeigt Ihnen, wann und wie Sie die Integration über ein Volumen durch Integration über Flächen oder über Kurven ausdrücken können. Diese Zusammenhänge sind für physikalische und technische Themenbereiche wie die Strömungsmechanik oder die Theorie elektromagnetischer Felder wichtig.
Teil III: Gewöhnliche Differentialgleichungen
Viele mathematische Modelle in den Naturwissenschaften werden mit Hilfe von Differentialgleichungen formuliert. Dies sind Gleichungen, in denen eine oder mehrere gesuchte Funktionen und ihre Ableitungen in Beziehung zueinander gesetzt werden.
Im Gegensatz zu den ersten beiden Teilen werden in diesem Teil dabei ausschließlich Funktionen von einer eindimensionalen Variablen betrachtet, dies führt zum Gebiet der gewöhnlichen Differentialgleichungen.
Nach einer Einführung zu diesem Thema in Kapitel 10werden in Kapitel 11Methoden zur Lösung bestimmter Differentialgleichungen behandelt, in denen außer der gesuchten Funktion nur ihre erste Ableitung auftritt. Kapitel 12erweitert die behandelten Problemstellungen auf eine besonders wichtige Sorte von Differentialgleichungen mit höheren Ableitungen, die linearen Differentialgleichungen. Leider gibt es nur für einige Spezialfälle solcher linearer Differentialgleichungen Standardlösungsverfahren. Diese werden in Kapitel 13beschrieben.
Als abschließendes Thema in diesem Teil werden in Kapitel 14Systeme von linearen Differentialgleichungen und Methoden zu ihrer Lösung beschrieben. Diese Systeme ähneln in gewisser Hinsicht einem linearen Gleichungssystem, wie es aus der linearen Algebra bekannt ist. Allerdings sind die gesuchten Größen hier unbekannte Funktionen und keine Vektoren.
Teil IV: Funktionentheorie
Die komplexe Analysis ist das Thema in Teil IV. Hierbei geht es um komplexwertige Funktionen einer komplexen Variablen, und es werden die Begriffe der eindimensionalen reellen Analysis auf solche Funktionen übertragen.
Kapitel 15führt die Grundlagen der Differentialrechnung in der komplexen Analysis ein, Kapitel 16liefert diese für die komplexe Integralrechnung. Diese ist mit der Integralrechnung für zweidimensionale reelle Funktionen verwandt. Einen besonderen Schwerpunkt bilden dabei die komplexen Kurvenintegrale und die Residuenmethode zur Berechnung solcher Integrale.
In Kapitel 17werden komplexe Potenzreihen und deren Verallgemeinerung zu Laurentreihen untersucht. Wie in der reellen Analysis helfen solche Reihenentwicklungen oft bei der Untersuchung der analytischen Eigenschaften einer gegebenen Funktion.
Im Top-Ten-Teil finden Sie einen kleinen Leitfaden, wie Sie mit einem Mathematikkurs an der Uni am besten zurechtkommen können.
Читать дальше

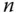 -dimensionale Teilmengen eines
-dimensionale Teilmengen eines 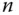 -dimensionalen Raums integrieren, sondern auch über niedriger dimensionale Teilmengen: Sie können Raum-, Flächen- und Kurvenintegrale definieren und berechnen. Die letzten beiden Sorten von Integralen unterscheiden sich noch einmal je nach Art der Integrandenfunktion: Vektorwertige Funktionen benötigen eine andere Art der Integration als skalarwertige Funktionen.
-dimensionalen Raums integrieren, sondern auch über niedriger dimensionale Teilmengen: Sie können Raum-, Flächen- und Kurvenintegrale definieren und berechnen. Die letzten beiden Sorten von Integralen unterscheiden sich noch einmal je nach Art der Integrandenfunktion: Vektorwertige Funktionen benötigen eine andere Art der Integration als skalarwertige Funktionen.










