positiv semidefinit , falls für alle ,
positiv definit , falls für alle ,
negativ semidefinit , falls für alle ,
negativ definit , falls für alle ,
indefinit in allen anderen Fällen.
Anhand der Definition ist die Definitheit einer gegebenen Matrix meistens nicht so einfach zu erkennen. Es gibt aber einige Berechnungsmethoden dazu, mit deren Hilfe Sie eine gegebene Matrix auf Definitheit prüfen können. Die zuverlässigste Methode verwendet dazu die Eigenwerte der Matrix.
 Für eine gegebene
Für eine gegebene  -Matrix
-Matrix 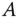 werden beim Eigenwertproblem ein Vektor
werden beim Eigenwertproblem ein Vektor 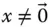 und ein
und ein 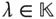 gesucht, sodass
gesucht, sodass
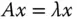
ist. Ein solches 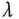 heißt Eigenwert von
heißt Eigenwert von 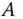 . Jeder Vektor
. Jeder Vektor 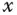 , der die obige Gleichung mit
, der die obige Gleichung mit 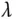 erfüllt, heißt Eigenvektor von
erfüllt, heißt Eigenvektor von 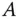 zum Eigenwert
zum Eigenwert 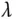 .
.
 Die Gleichung
Die Gleichung 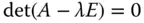 heißt die charakteristische Gleichung von
heißt die charakteristische Gleichung von 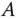 .
.
Das Polynom 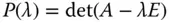 heißt das charakteristische Polynom der Matrix
heißt das charakteristische Polynom der Matrix 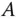 .
.
Die Lösungen der charakteristischen Gleichung 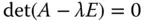 einer
einer  -Matrix
-Matrix 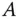 und damit die Eigenwerte von
und damit die Eigenwerte von 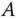 sind nichts anderes als die Nullstellen des charakteristischen Polynoms.
sind nichts anderes als die Nullstellen des charakteristischen Polynoms.
 Zur Bestimmung der Definitheit einer symmetrischen Matrix betrachten Sie die Eigenwerte dieser Matrix. Ist
Zur Bestimmung der Definitheit einer symmetrischen Matrix betrachten Sie die Eigenwerte dieser Matrix. Ist 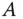 eine symmetrische Matrix mit den Eigenwerten
eine symmetrische Matrix mit den Eigenwerten 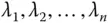 , dann ist
, dann ist 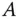 :
:
positiv semidefinit genau dann, wenn für ,
positiv definit genau dann, wenn für ,
negativ semidefinit genau dann, wenn für ,
negativ definit genau dann, wenn für .
Die Eigenvektoren 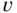 zu einem gegebenen Eigenwert
zu einem gegebenen Eigenwert 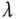 einer Matrix
einer Matrix 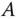 berechnen Sie mit Hilfe des Gauß-Verfahrens aus dem Abschnitt »Lineare Gleichungssysteme und das Gauß-Verfahren« zu dem linearen Gleichungssystem
berechnen Sie mit Hilfe des Gauß-Verfahrens aus dem Abschnitt »Lineare Gleichungssysteme und das Gauß-Verfahren« zu dem linearen Gleichungssystem
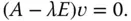
Dabei entsteht die Matrix dieses Gleichungssystems einfach dadurch, dass Sie in der Diagonale von 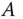 den Eigenwert
den Eigenwert 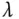 abziehen.
abziehen.
 Beim Lösen des Gleichungssystems für die Eigenvektoren dürfen Sie die triviale Lösung, den Nullvektor, nicht als Eigenvektor wählen! Mit dem Gauß-Verfahren müssen Sie allerdings mindestens eine ganze Nullzeile erzeugen können. Das heißt: Es muss mindestens eine eindimensionale Lösungsmenge für dieses System geben. Sie haben also unendlich viele Lösungen als Eigenvektoren zur Wahl.
Beim Lösen des Gleichungssystems für die Eigenvektoren dürfen Sie die triviale Lösung, den Nullvektor, nicht als Eigenvektor wählen! Mit dem Gauß-Verfahren müssen Sie allerdings mindestens eine ganze Nullzeile erzeugen können. Das heißt: Es muss mindestens eine eindimensionale Lösungsmenge für dieses System geben. Sie haben also unendlich viele Lösungen als Eigenvektoren zur Wahl.
Die eindimensionale Analysis beschäftigt sich mit reellwertigen Funktionen einer reellen Variablen 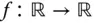 . Im Wesentlichen wird das Änderungsverhalten solcher Funktionen untersucht: Wie ändern sich die Funktionswerte
. Im Wesentlichen wird das Änderungsverhalten solcher Funktionen untersucht: Wie ändern sich die Funktionswerte 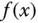 , wenn das Argument
, wenn das Argument 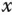 geändert wird? Solche Untersuchungen werden in der Mathematik mit Hilfe geeigneter Folgen und ihrer Grenzwerte durchgeführt. Dies liefert Begriffe wie Stetigkeit und Differenzierbarkeit und gibt Ihnen geeignete Methoden zur Extremstellensuche. Selbst der Integralbegriff und Näherungsmethoden wie die Taylorreihenentwicklung beruhen auf Grenzwerten. Folgen und ihr Verhalten bilden die Grundlage der ganzen Analysis und sind damit auch die Grundlage für die erfolgreiche mathematische Beschreibung der Welt. Dies ist auch in der mehrdimensionalen Analysis der Fall, die in den folgenden Kapiteln näher beschrieben wird. Grund genug, hier einen kurzen Überblick über Folgen und Grenzwerte zu geben.
geändert wird? Solche Untersuchungen werden in der Mathematik mit Hilfe geeigneter Folgen und ihrer Grenzwerte durchgeführt. Dies liefert Begriffe wie Stetigkeit und Differenzierbarkeit und gibt Ihnen geeignete Methoden zur Extremstellensuche. Selbst der Integralbegriff und Näherungsmethoden wie die Taylorreihenentwicklung beruhen auf Grenzwerten. Folgen und ihr Verhalten bilden die Grundlage der ganzen Analysis und sind damit auch die Grundlage für die erfolgreiche mathematische Beschreibung der Welt. Dies ist auch in der mehrdimensionalen Analysis der Fall, die in den folgenden Kapiteln näher beschrieben wird. Grund genug, hier einen kurzen Überblick über Folgen und Grenzwerte zu geben.
Читать дальше

 Für eine gegebene
Für eine gegebene  -Matrix
-Matrix 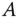 werden beim Eigenwertproblem ein Vektor
werden beim Eigenwertproblem ein Vektor 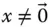 und ein
und ein 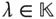 gesucht, sodass
gesucht, sodass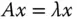
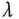 heißt Eigenwert von
heißt Eigenwert von 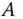 . Jeder Vektor
. Jeder Vektor 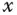 , der die obige Gleichung mit
, der die obige Gleichung mit 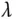 erfüllt, heißt Eigenvektor von
erfüllt, heißt Eigenvektor von 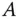 zum Eigenwert
zum Eigenwert 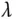 .
.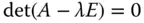 heißt die charakteristische Gleichung von
heißt die charakteristische Gleichung von 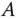 .
.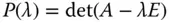 heißt das charakteristische Polynom der Matrix
heißt das charakteristische Polynom der Matrix 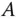 .
.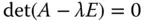 einer
einer  -Matrix
-Matrix 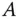 und damit die Eigenwerte von
und damit die Eigenwerte von 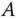 sind nichts anderes als die Nullstellen des charakteristischen Polynoms.
sind nichts anderes als die Nullstellen des charakteristischen Polynoms. Zur Bestimmung der Definitheit einer symmetrischen Matrix betrachten Sie die Eigenwerte dieser Matrix. Ist
Zur Bestimmung der Definitheit einer symmetrischen Matrix betrachten Sie die Eigenwerte dieser Matrix. Ist 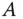 eine symmetrische Matrix mit den Eigenwerten
eine symmetrische Matrix mit den Eigenwerten 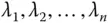 , dann ist
, dann ist 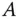 :
: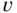 zu einem gegebenen Eigenwert
zu einem gegebenen Eigenwert 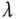 einer Matrix
einer Matrix 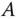 berechnen Sie mit Hilfe des Gauß-Verfahrens aus dem Abschnitt »Lineare Gleichungssysteme und das Gauß-Verfahren« zu dem linearen Gleichungssystem
berechnen Sie mit Hilfe des Gauß-Verfahrens aus dem Abschnitt »Lineare Gleichungssysteme und das Gauß-Verfahren« zu dem linearen Gleichungssystem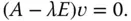
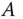 den Eigenwert
den Eigenwert 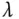 abziehen.
abziehen. Beim Lösen des Gleichungssystems für die Eigenvektoren dürfen Sie die triviale Lösung, den Nullvektor, nicht als Eigenvektor wählen! Mit dem Gauß-Verfahren müssen Sie allerdings mindestens eine ganze Nullzeile erzeugen können. Das heißt: Es muss mindestens eine eindimensionale Lösungsmenge für dieses System geben. Sie haben also unendlich viele Lösungen als Eigenvektoren zur Wahl.
Beim Lösen des Gleichungssystems für die Eigenvektoren dürfen Sie die triviale Lösung, den Nullvektor, nicht als Eigenvektor wählen! Mit dem Gauß-Verfahren müssen Sie allerdings mindestens eine ganze Nullzeile erzeugen können. Das heißt: Es muss mindestens eine eindimensionale Lösungsmenge für dieses System geben. Sie haben also unendlich viele Lösungen als Eigenvektoren zur Wahl.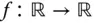 . Im Wesentlichen wird das Änderungsverhalten solcher Funktionen untersucht: Wie ändern sich die Funktionswerte
. Im Wesentlichen wird das Änderungsverhalten solcher Funktionen untersucht: Wie ändern sich die Funktionswerte 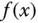 , wenn das Argument
, wenn das Argument 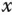 geändert wird? Solche Untersuchungen werden in der Mathematik mit Hilfe geeigneter Folgen und ihrer Grenzwerte durchgeführt. Dies liefert Begriffe wie Stetigkeit und Differenzierbarkeit und gibt Ihnen geeignete Methoden zur Extremstellensuche. Selbst der Integralbegriff und Näherungsmethoden wie die Taylorreihenentwicklung beruhen auf Grenzwerten. Folgen und ihr Verhalten bilden die Grundlage der ganzen Analysis und sind damit auch die Grundlage für die erfolgreiche mathematische Beschreibung der Welt. Dies ist auch in der mehrdimensionalen Analysis der Fall, die in den folgenden Kapiteln näher beschrieben wird. Grund genug, hier einen kurzen Überblick über Folgen und Grenzwerte zu geben.
geändert wird? Solche Untersuchungen werden in der Mathematik mit Hilfe geeigneter Folgen und ihrer Grenzwerte durchgeführt. Dies liefert Begriffe wie Stetigkeit und Differenzierbarkeit und gibt Ihnen geeignete Methoden zur Extremstellensuche. Selbst der Integralbegriff und Näherungsmethoden wie die Taylorreihenentwicklung beruhen auf Grenzwerten. Folgen und ihr Verhalten bilden die Grundlage der ganzen Analysis und sind damit auch die Grundlage für die erfolgreiche mathematische Beschreibung der Welt. Dies ist auch in der mehrdimensionalen Analysis der Fall, die in den folgenden Kapiteln näher beschrieben wird. Grund genug, hier einen kurzen Überblick über Folgen und Grenzwerte zu geben.










