J. Michael Fried - Mathematik für Ingenieure II für Dummies

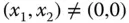Für gilt nach den Ableitungsregeln für gewöhnliche Ableitungen: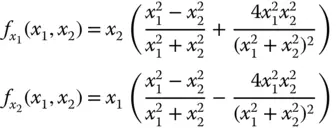

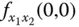Berechnen Sie zum Beispiel die partielle Ableitung als partielle Ableitung von 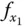nach 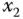an der Stelle 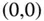, dann erhalten Sie nach der Grenzwertdefinition der Ableitung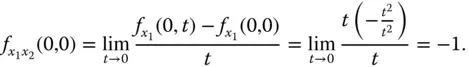

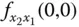Umgekehrt ist die partielle Ableitung von 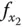nach 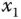an der Stelle 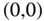. Nach Grenzwertdefinition erhalten Sie daher: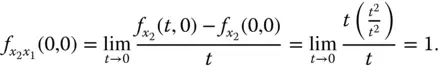

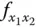Die beiden gemischten partiellen Ableitungen 2. Ordnung und 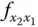sind also nicht gleich, es kommt auf die Reihenfolge der einzelnen Ableitungen an.

Falls die betrachteten partiellen Ableitungen Unstetigkeitsstellen besitzen, müssen Sie bei der Berechnung höherer partieller Ableitungen die Reihenfolge der einzelnen Ableitungen beachten.

Das ist lästig, denn selbst eine reellwertige Funktion von nur zwei Variablen hat zum Beispiel schon acht möglicherweise unterschiedliche partielle Ableitungen 3. Ordnung, die Sie im Prinzip alle einzeln berechnen müssen.

Im Zusammenhang mit höheren partiellen Ableitungen ist eine Eigenschaft besonders nützlich: stetige partielle Differenzierbarkeit.

Eine Funktion 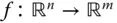heißt auf einer Menge 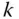-mal stetig partiell differenzierbar , wenn für alle 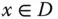die partiellen Ableitungen bis zur 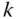-ten Ordnung existieren und auf 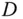stetig sind.

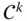Eine solche Funktion wird eine - Funktion auf genannt, in Formeln:

Stetig partiell differenzierbare Funktionen werden oft glatte Funktionen genannt. Je öfter eine Funktion stetig partiell differenzierbar ist, desto glatter ist sie.

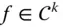
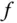Die Berechnung der höheren partiellen Ableitungen einer Funktion vereinfacht sich, falls 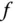glatt genug ist.

Der Satz von Schwarz: Ist 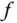auf einer offenen Menge 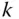-mal stetig partiell differenzierbar, dann können Sie die Reihenfolge der partiellen Differentiationen aller partiellen Ableitungen der Ordnungen beliebig vertauschen.

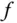Sie müssen bei einer glatten Funktion daher nicht jede höhere partielle Ableitung einzeln berechnen, sondern erhalten einige direkt durch Vertauschung der Differentiationsreihenfolge aus anderen partiellen Ableitungen. Ist zum Beispiel eine 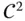-Funktion, dann gilt für alle 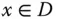und alle :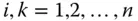